くさび形空気層による光の干渉とは
本項では、以下の内容について解説しています。
- ・くさび形空気層の干渉の原理
- ・明暗の条件、干渉縞の間隔の導出
- ・下面から見たときの明暗の条件
- ・計算問題
【1】くさび形空気層における光の干渉
くさび形空気層における光の干渉とは、図1のように2枚のガラス板を一辺を接した状態で、くさび形に配置したときに観察される干渉縞のことをいいます。
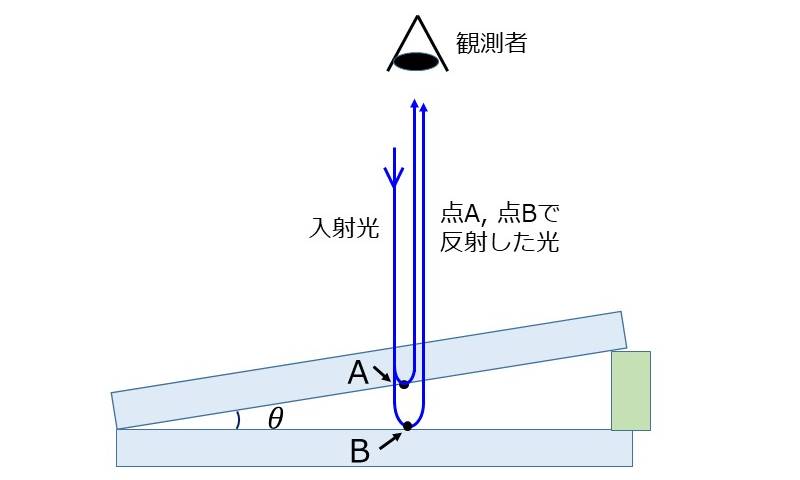
2枚のガラスの上方から光を照射すると、くさび形の空気層の前後で光が分割されることで、干渉縞が観測されます。
照射された光は、1枚目のガラスの裏面(点A)において反射光と透過光に分かれます。点Aで透過した光は、2枚目のガラスの表面(点B)で反射された後、再び点Aで透過し、元の入射側の領域に戻ります。
点Aで反射した光と、点Bで反射した光が干渉することにより、干渉縞が観察されます。
図2にくさび形の空気層による光の干渉を、上から見たときの干渉縞のイメージ図を示します。

図2は干渉縞の光強度の大小を色で表示しています。黒い色が干渉の弱め合いにより暗く見える箇所、白い色が強め合いにより明るく見える箇所を表しています。
図2のように、くさび形の空気層による光の干渉は、周期的に明るさの強弱が繰り返されることが分かります。
【1-1】光路差の計算
ここで、点Aで反射する光と、点Bで反射する光の光路差を求めます。
図3のように、2枚目のガラス板と平行にx軸を取り、ガラス板の接点を\(\hspace{2pt}\large{x=0}\hspace{2pt}\)とします。
また、2枚のガラス板のなす角度を\(\hspace{2pt}\large{\theta}\hspace{2pt}\)、接点から距離\(\hspace{2pt}\large{L}\hspace{2pt}\)において\(\hspace{2pt}\large{D}\hspace{2pt}\)の間隔が取られているとします。
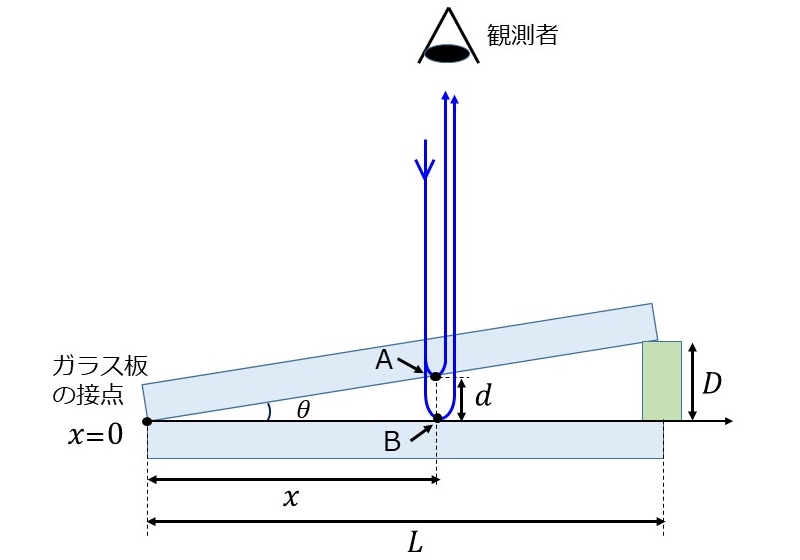
このとき、位置\(\hspace{2pt}\large{x}\hspace{2pt}\)における光路差は、点Aから点Bの距離を\(\hspace{2pt}\large{d}\hspace{2pt}\)とすると、点AB間を往復する距離であるため\(\hspace{2pt}\large{2d}\hspace{2pt}\)となります。
ここで、距離\(\hspace{2pt}\large{d}\hspace{2pt}\)は、\(\hspace{2pt}\large{d = x \tan \theta}\hspace{2pt}\)の関係があるため、光路差\(\hspace{2pt}\large{2d}\hspace{2pt}\)は以下のように求められます。 $$\large{2d = 2 x \tan \theta}$$
また、\(\hspace{2pt}\large{\displaystyle \tan \theta = \frac{D}{L}}\hspace{2pt}\)の関係があるので、光路差\(\hspace{2pt}\large{2d}\hspace{2pt}\)は以下のように書き表すこともできます。 $$\large{2d = \frac{2 D}{L} x}$$
【1-2】干渉縞の明暗の条件
ここで、干渉縞の明暗の条件を導出します。
点Aと点Bにおける反射は、屈折率の大小関係によって位相が変化します。
点Aにおける反射では、屈折率の大きい物質から小さい物質への反射となり、位相は変化しません(自由端反射)。
一方、点Bにおける反射では、屈折率の小さい物質から大きい物質への反射となり、位相は\(\hspace{2pt}\large{\pi}\hspace{2pt}\)だけ変化します(固定端反射)。
位相が\(\hspace{2pt}\large{\pi}\hspace{2pt}\)だけズレるときの強め合い、弱め合いの条件は光路差\(\hspace{2pt}\large{2d}\hspace{2pt}\)、光の波長\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)を用いて以下のように表されます。
\(\hspace{2pt}\large{\displaystyle 2d = \left(m +\frac{1}{2} \right) \lambda\hspace{10pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
\(\hspace{2pt}\large{\displaystyle 2d = m \lambda\hspace{10pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
したがって、くさび形空気層で発生する光路差は\(\hspace{2pt}\large{2d = 2x \tan \theta = \frac{2 D}{L} x }\hspace{2pt}\)であるため、以下のように縞の明暗の条件が求められます。
\(\hspace{2pt}\large{\displaystyle 2x \tan \theta = \left(m +\frac{1}{2} \right) \lambda\hspace{10pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
もしくは\(\hspace{2pt}\large{\tan \theta = \frac{D}{L}}\hspace{2pt}\)より
\(\hspace{2pt}\large{\displaystyle \frac{2 D}{L} x = \left(m +\frac{1}{2} \right) \lambda\hspace{10pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
また、弱め合う干渉が発生する条件は以下のように計算されます。
\(\hspace{2pt}\large{\displaystyle 2x \tan \theta = m \lambda\hspace{10pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
もしくは\(\hspace{2pt}\large{\tan \theta = \frac{D}{L}}\hspace{2pt}\)より
\(\hspace{2pt}\large{\displaystyle \frac{2 D}{L} x = m \lambda\hspace{10pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
ここで、暗い縞を例として、明暗の条件の整数\(\hspace{2pt}\large{m}\hspace{2pt}\)と、実際に観測される縞の位置\(\hspace{2pt}\large{x_m}\hspace{2pt}\)がどのような関係にあるのかを図4に示します。
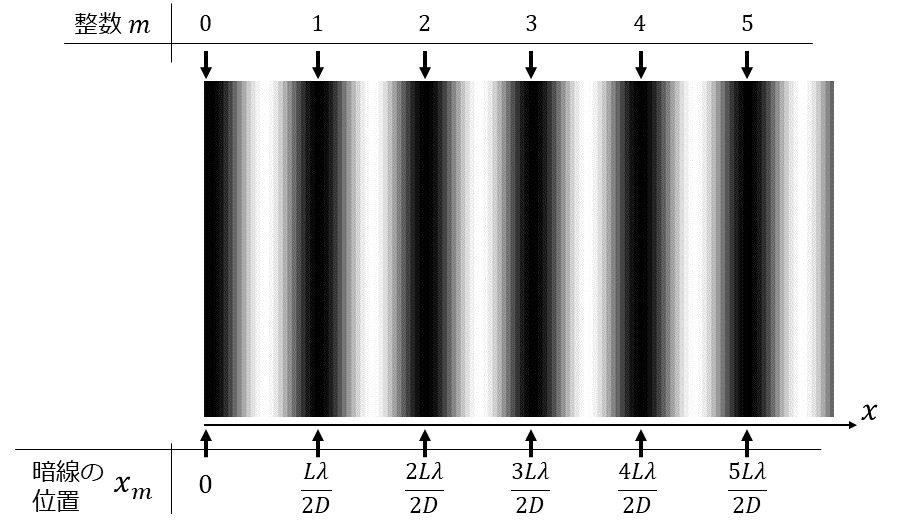
図4の最も左側が、2枚のガラスの接点(\(\hspace{2pt}\large{x=0}\hspace{2pt}\))を表しています。この\(\hspace{2pt}\large{x=0}\hspace{2pt}\)の位置に、\(\hspace{2pt}\large{m=0}\hspace{2pt}\)の暗い縞が位置します。
【1-3】干渉縞の縞間隔の導出
本章では、観測される干渉縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)の求め方について解説します。
以下の図5のように、干渉縞の縞間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)は、ある整数\(\hspace{2pt}\large{m}\hspace{2pt}\)のおける暗線の位置\(\hspace{2pt}\large{x_m}\hspace{2pt}\)と、整数\(\hspace{2pt}\large{m+1}\hspace{2pt}\)における暗線の位置\(\hspace{2pt}\large{x_{m+1}}\hspace{2pt}\)の差分を計算することにより求められます。
(明線の条件から求めても結果は同じです。)
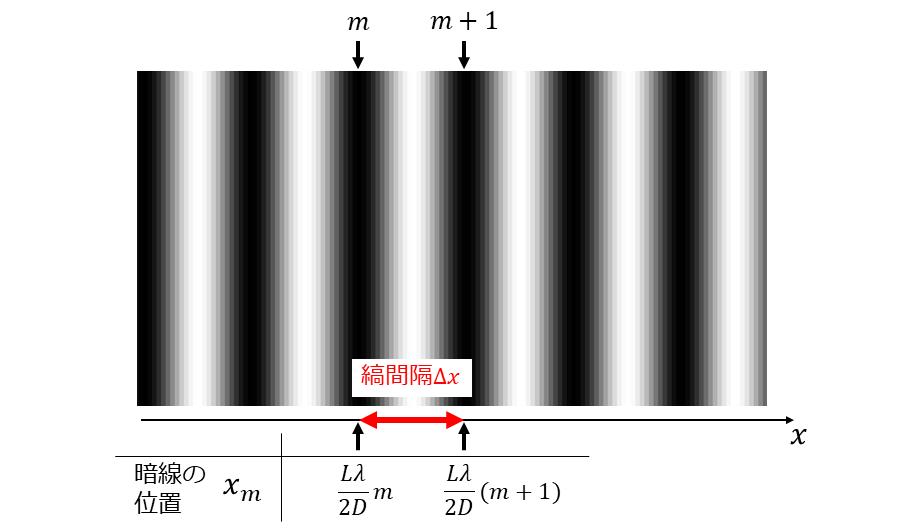
ここで、整数\(\hspace{2pt}\large{m}\hspace{2pt}\)における暗線の位置\(\hspace{2pt}\large{x_m}\hspace{2pt}\)は弱め合いの条件から以下のように求められます。 $$\large{\frac{2 D}{L} x_m = m \lambda}$$ 上式を\(\hspace{2pt}\large{x_m}\hspace{2pt}\)について解くと以下のようになります。 $$\large{x_m = \frac{L \lambda m}{2 D}}$$
したがって、縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)は以下のように計算されます。 \begin{eqnarray} \large \Delta x &\large =&\large x_{m+1} - x_{m}\\[1em] &\large =&\large\frac{L \lambda (m+1)}{2 D} - \frac{L \lambda m}{2 D} \\[0.5em] &\large =&\large \frac{L \lambda}{2 D} \end{eqnarray}
また、\(\hspace{2pt}\large{ \tan \theta = \frac{D}{L}}\hspace{2pt}\)の関係があるので、縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)は以下のようにも表せます。 $$\large \Delta x = \frac{ \lambda}{2 \tan \theta}$$
上式から、観測される干渉縞の間隔は、以下の3つの性質があることが分かります。
・『(縞の間隔が整数\(\hspace{2pt}\large{m}\hspace{2pt}\)に依存しないため、)観察される縞の間隔は全て一定の値となる』
・『2枚のガラス板のなす角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)が大きいほど(間隔\(\hspace{2pt}\large{D}\hspace{2pt}\)が大きいほど)、縞の間隔は狭くなる』
・『入射する光の波長\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)が長いほど、縞の間隔は広くなる』
【2】くさび形空気層の下から見たときの干渉
本章では、図6のようなくさび形空気層の下面から透過する光の干渉について考えます。
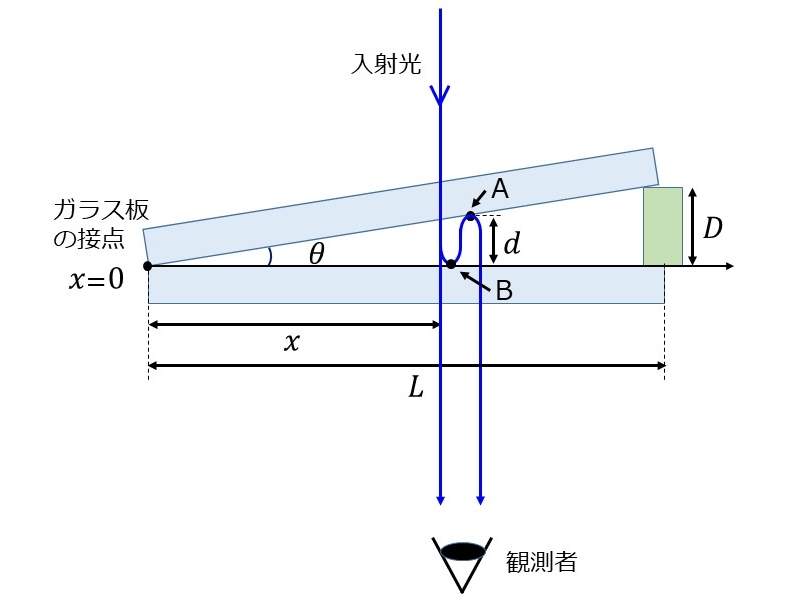
【2-1】光路差の計算
図6で示しているように、透過光の場合は2枚のガラス板を透過した光と、2回くさび形空気層で反射した光での反射となります。
このとき発生する光路差は、点Bから点Aを往復する距離であるため、上から見た場合と同様に\(\hspace{2pt}\large{2d}\hspace{2pt}\)となります。
したがって、光路差\(\hspace{2pt}\large{2d}\hspace{2pt}\)は以下のようになります。
$$\large{2d = 2 x \tan \theta}$$
また、\(\hspace{2pt}\large{\displaystyle \tan \theta = \frac{D}{L}}\hspace{2pt}\)の関係があるので、光路差\(\hspace{2pt}\large{2d}\hspace{2pt}\)は以下のように書き表すこともできます。 $$\large{2d = \frac{2 D}{L} x}$$
【2-2】干渉縞の明暗の条件
下面から観測する場合の位相差について考えます。
下面から観察した場合、点Bで反射した光線は、再び点Aで反射されます。
このとき、2回の反射はどちらも屈折率の小さい物質から大きい物質での反射であり、それぞれの反射で位相が\(\hspace{2pt}\large{\pi}\hspace{2pt}\)だけ反射します(固定端反射)。
したがって、上面から見たときと同様に計算すると、明暗の条件は以下のようになります。
\(\large{\displaystyle 2 x \tan \theta = m \lambda\hspace{5pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
もしくは\(\displaystyle\hspace{2pt}\large{\tan \theta = \frac{D}{L}}\hspace{2pt}\)より
\(\large{\displaystyle \frac{2 D}{L} x = m \lambda\hspace{5pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
\(\large{\displaystyle 2 x \tan \theta = \frac{1}{2}(2m +1) \lambda\hspace{5pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
もしくは\(\displaystyle\hspace{2pt}\large{\tan \theta = \frac{D}{L}}\hspace{2pt}\)より
\(\large{\displaystyle \frac{2 D}{L} x = \frac{1}{2}(2m +1) \lambda\hspace{5pt} (m=0,1,2, \cdots)}\hspace{2pt}\)
上面と下面から見たときで干渉縞の発生条件を比較すると、明暗の条件が逆転していることが分かります。
例えば、上面から観察したときに位置\(\hspace{2pt}\large{x}\hspace{2pt}\)に明るい縞が観察された場合、下面から見たときには位置\(\hspace{2pt}\large{x}\hspace{2pt}\)には暗い縞が観測されます。
この上面と下面で干渉縞の明暗が反転する性質は、エネルギーの保存則を表しています。
例えば、上から見て明るい縞が発生しているとき、干渉の効果がない場合と比較して観測される光強度は大きくなります。上方向に光強度が大きくなった分だけ、下方向は光強度が減少して暗い縞が観測されます。
【3】くさび形空気層の干渉の計算問題
本章では、くさび形空気層の干渉に関連した計算問題を解説します。
【3-1】縞の発生する位置
【問題】
2枚のガラス板からなるくさび形空気層にd線(\(\hspace{2pt}\large{\lambda=589.3[nm]}\hspace{2pt}\))の波長の光を入射する。上面から観測したとき、2枚のガラスの接点から数えて100番目の明線はどの位置に発生するか。
なお、図7に示すように、2枚のガラス板の接点から200[mm]の位置に高さ0.3[mm]のスペーサーを挟んでいるとする。
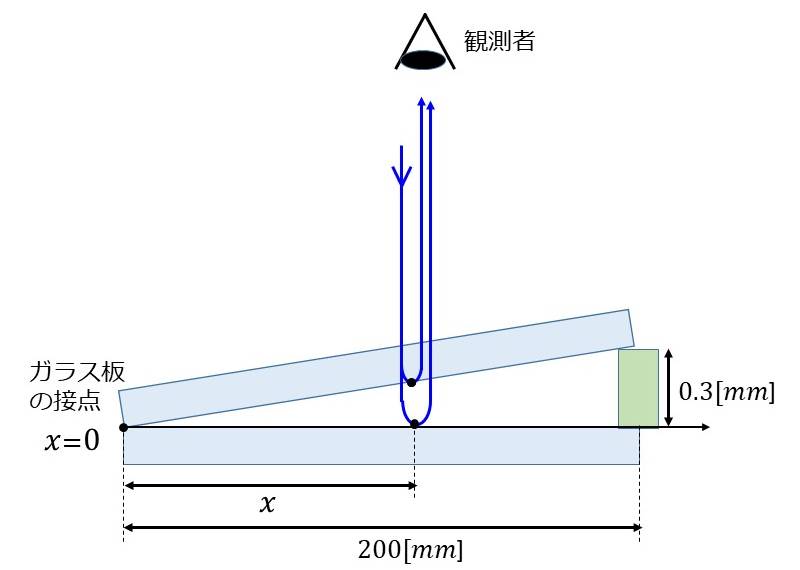
【解答と解説】
くさび形空気層の上面から観測したときに、明るい縞の発生する条件は以下となります。
$$\large{\frac{2 D}{L} x = \frac{1}{2}(2m +1) \lambda\hspace{10pt} (m=0,1,2, \cdots)}$$
\(\hspace{2pt}\large{m=0}\hspace{2pt}\)のとき、1番目の明るい縞が発生することから、100番目の明るい縞は\(\hspace{2pt}\large{m=99}\hspace{2pt}\)のとき発生します。
したがって、100番目の明るい縞の発生位置\(\hspace{2pt}\large{x}\hspace{2pt}\)は以下のようにして求められます。
【3-2】2枚のガラス板の距離が離れた場合
【問題】
図8のように2枚のガラス板が角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)を保ったまま距離\(\hspace{2pt}\large{a}\hspace{2pt}\)だけ離れたとする。このとき、離れる前と比較して、上方から見た明るい縞の発生位置はどのように変化するか。
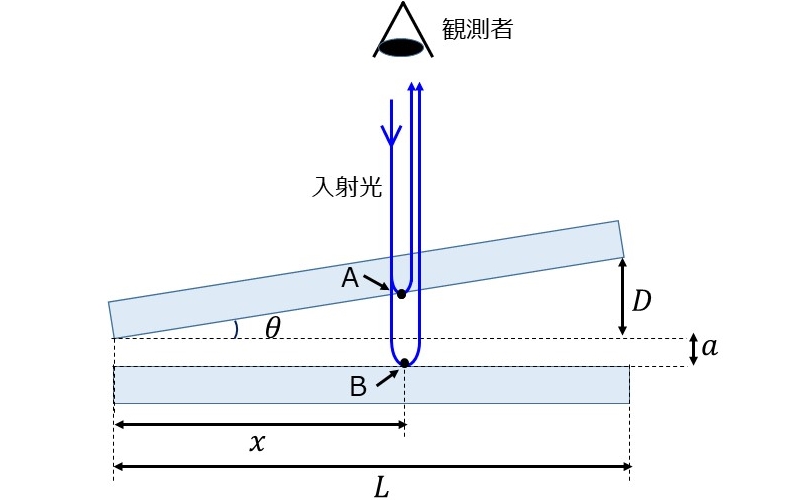
【回答と解説】
2枚のガラス板が離れていないとき(\(\hspace{2pt}\large{a=0}\hspace{2pt}\))、位置\(\hspace{2pt}\large{x}\hspace{2pt}\)にある整数\(\hspace{2pt}\large{m}\hspace{2pt}\)における明るい縞が発生したとすると、強め合いの条件から以下が成り立ちます。 $$\large{\frac{2 D}{L} x = \frac{1}{2}(2m +1) \lambda\hspace{10pt}(1)}$$
ここで、2枚のガラス板が距離\(\hspace{2pt}\large{a}\hspace{2pt}\)だけ離れたとき、位置\(\hspace{2pt}\large{x + \Delta x}\hspace{2pt}\)の位置に整数\(\hspace{2pt}\large{m}\hspace{2pt}\)における明るい縞が発生したとします。
このとき、光路差が\(\hspace{2pt}\large{\displaystyle \frac{2 D}{L} x +2a}\hspace{2pt}\)となることから、(1)式と同じ整数\(\hspace{2pt}\large{m}\hspace{2pt}\)の明るい縞は以下の式を満たします。
$$\large{\frac{2 D}{L} (x + \Delta x) +2a = \frac{1}{2}(2m +1) \lambda\hspace{10pt}(2)}$$
(1)式と(2)式を解いて、整数\(\hspace{2pt}\large{m}\hspace{2pt}\)の明るい縞の移動距離\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)を求めると、以下のようになります。 $$\large{\Delta x = -\frac{L}{D}a}$$
したがって、縞の発生位置\(\hspace{2pt}\large{x}\hspace{2pt}\)は、ガラス板が距離\(\hspace{2pt}\large{a}\hspace{2pt}\)だけ離れたときに、\(\hspace{2pt}\large{\displaystyle \frac{L}{D}a}\hspace{2pt}\)だけガラス板の接点に近づくことが分かります。
【3-3】くさび形空気層を水で満たした場合の縞間隔
【問題】
図9のように、屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)の2枚のガラス板によるくさび形空気層を、屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の水で満たしたとする。このとき、上から見たときの干渉縞の間隔はどのように変化するか?
ただし、屈折率は\(\hspace{2pt}\large{n_1 > n_2}\hspace{2pt}\)の関係であるとする。
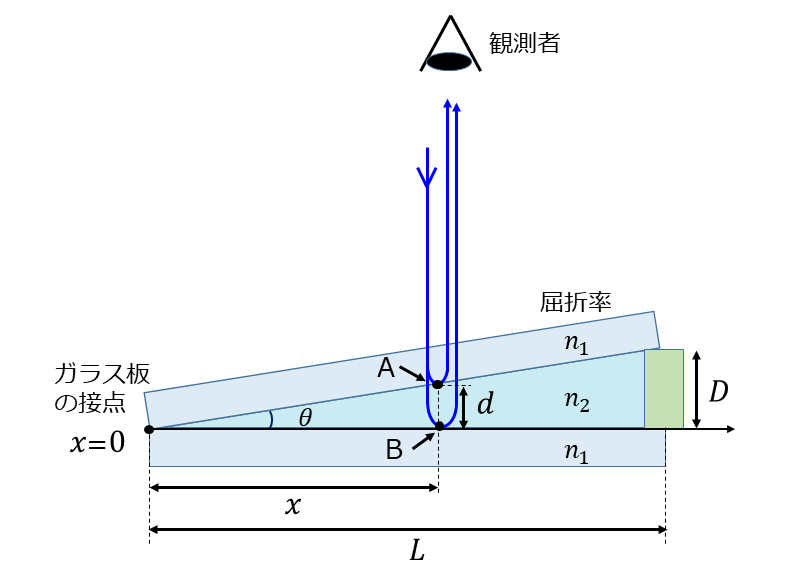
【回答と解説】
点Aと点Bにおける反射は、屈折率の大小関係によって位相が変化するため、まず位相の変化について確認します。
点Aにおける反射では、\(\hspace{2pt}\large{n_1 > n_2}\hspace{2pt}\)の条件から、屈折率の大きい物質から小さい物質に向かう反射となり、位相は変化しません
一方、点Bにおける反射では、\(\hspace{2pt}\large{n_1 > n_2}\hspace{2pt}\)の条件から、屈折率の小さい物質から大きい物質に向かう反射となり、位相は\(\hspace{2pt}\large{\pi}\hspace{2pt}\)だけ変化します。
よって、屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の水でくさび形空気層を満たしても、水で満たす前と位相の変化の仕方は同じであることが分かります。
つまり、【1-2】干渉縞の明暗の条件と同じく、光路差\(\hspace{2pt}\large{2d}\hspace{2pt}\)が波長の\(\hspace{2pt}\large{m+\frac{1}{2}}\hspace{2pt}\)倍のとき強め合う干渉、波長の\(\hspace{2pt}\large{m}\hspace{2pt}\)倍のとき弱め合う干渉になります。
ここで、【1-3】干渉縞の縞間隔の導出と同様に縞間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)を求めます。
屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の水中を進行する光の波長は\(\hspace{2pt}\large{\lambda / n_2}\hspace{2pt}\)と換算されるため、暗い縞の条件から、以下が成り立ちます。 $$\large{\frac{2 D}{L} x_m = m \frac{\lambda}{n_2}}$$ 上式を\(\hspace{2pt}\large{x_m}\hspace{2pt}\)について解くと以下のようになります。 $$\large{x_m = \frac{L \lambda m}{2 D n_2}}$$
したがって、縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)は以下のように計算されます。 \begin{eqnarray} \large \Delta x &\large =&\large x_{m+1} - x_{m}\\[1.0em] &\large =&\large\frac{L \lambda (m+1)}{2 D n_2} - \frac{L \lambda m}{2 D n_2} \\[0.5em] &\large =&\large \frac{L \lambda}{2 D n_2} \end{eqnarray}
水を満たす前の縞間隔は\(\hspace{2pt}\large{\displaystyle \frac{L \lambda}{2 D}}\hspace{2pt}\)であるため、くさび形空気層に水を満たしたときの縞間隔は\(\hspace{2pt}\large{\displaystyle \frac{1}{n_2}}\hspace{2pt}\)の大きさとなります。