ニュートンリングとは
本項では、光の干渉の現象の1つであるニュートンリングと、その応用である曲率測定について解説します。
【1】ニュートンリングとは
ニュートンリングとは、球面レンズや平面ガラスを重ね合わせることで、同心円の干渉縞が発生する現象のことです。
図1のように平面ガラスの上に、球面レンズを置いた実験系を考えます。この実験系の上方から光を入射させることで、同心円の干渉縞が観測されます。
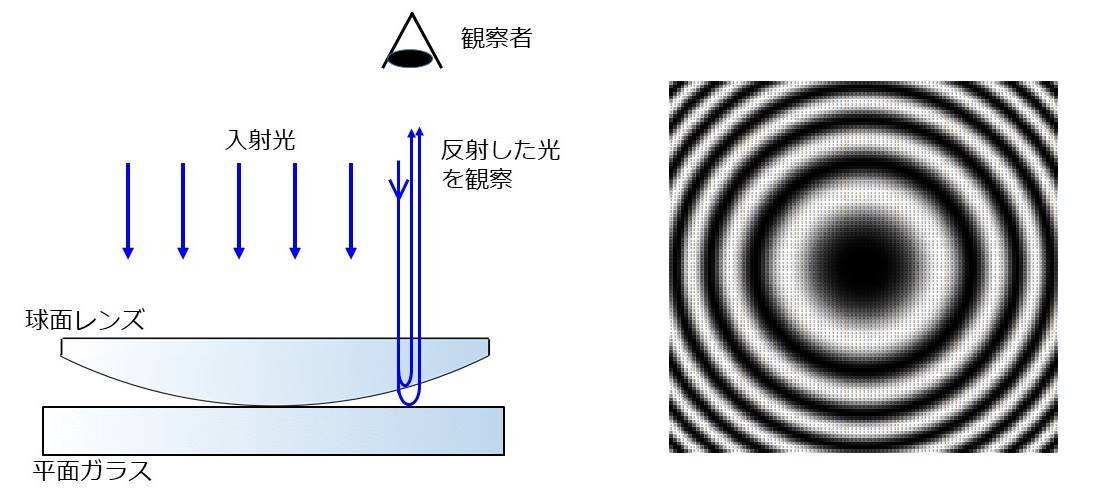
【1-1】間隔\(\hspace{2pt}\large{d}\hspace{2pt}\)と位置\(\hspace{2pt}\large{x}\hspace{2pt}\)の関係式の導出
図2に球面レンズと平面ガラスを重ね合わせたときの間隔\(\hspace{2pt}\large{d}\hspace{2pt}\)や位置\(\hspace{2pt}\large{x}\hspace{2pt}\)の関係を図示します。
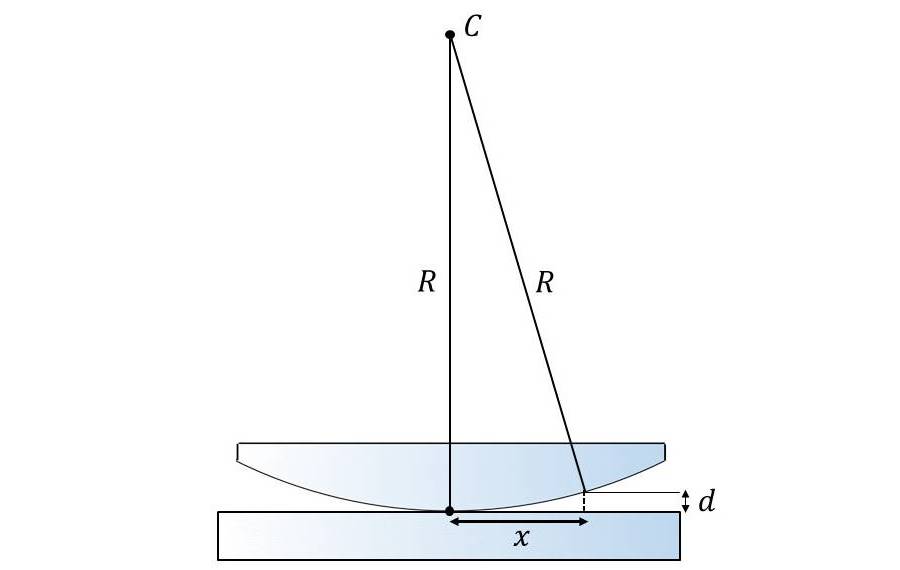
図2より、縞の発生条件を位置\(\hspace{2pt}\large{x}\hspace{2pt}\)の関数として求めるため、間隔\(\hspace{2pt}\large{d}\hspace{2pt}\)と位置\(\hspace{2pt}\large{x}\hspace{2pt}\)の関係式を求めます。
平面ガラスと球面レンズ面との間隔を\(\hspace{2pt}\large{d}\hspace{2pt}\)、球面レンズ面の曲率半径を\(\hspace{2pt}\large{R}\hspace{2pt}\)、平面ガラス上の中心からの距離を\(\hspace{2pt}\large{x}\hspace{2pt}\)とします。 また、球面の中心を点Cとしています。
図2より、間隔\(\hspace{2pt}\large{d}\hspace{2pt}\)、曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)、位置\(\hspace{2pt}\large{x}\hspace{2pt}\)は三平方の定理により以下のような関係にあります。 $$\large{R^2 = {(R-d)}^2 + x^2}$$ 上式を展開すると以下のようになります。 $$\large{2Rd = d^2 + x^2}$$ 間隔\(\hspace{2pt}\large{d}\hspace{2pt}\)は曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)より十分小さいとして、\(\hspace{2pt}\large{d^2 \approx 0}\hspace{2pt}\)と近似すると以下のようになります。 $$\large{d \approx \frac{x^2}{2R}\hspace{20pt}(1)}$$
【1-2】干渉縞の発生条件
ここで、図3のように球面で反射する光(点A)と、平面ガラスで反射する光(点B)の干渉する条件について考えます。
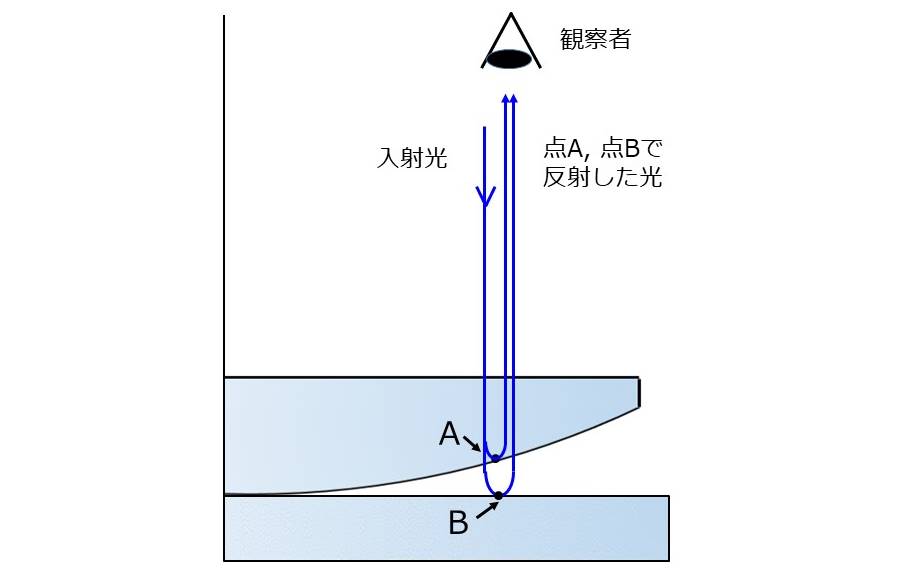
点Aでは、屈折率の大きい物質から小さい物質に向かって反射するため、位相の変化はありません(自由端反射)。
一方、点Bでは、点Aとは反対となり位相が\(\hspace{2pt}\large{\pi}\hspace{2pt}\)変化する反射となります。(固定端反射)
このとき、明るい縞の発生する条件は、位相変化を考慮して、光路長差が波長の長さの\(\hspace{2pt}\large{\frac{1}{2}(2m+1)}\hspace{2pt}\)倍(mは整数)であるため、以下のようになります。 $$\large{2d = \frac{1}{2}(2m+1) \lambda}$$ 間隔\(\hspace{2pt}\large{d}\hspace{2pt}\)に(1)式の結果を代入すると、平面ガラス上の位置\(\hspace{2pt}\large{x}\hspace{2pt}\)と明るい縞の発生する関係式が求められます。
\(\hspace{2pt}\large{\displaystyle x = \sqrt{\frac{1}{2}(2m+1) R \lambda}\hspace{10pt} (m=0,1,2,\cdots)}\hspace{2pt}\)
暗い縞の発生する条件は、光路長差が波長の長さの\(\hspace{2pt}\large{2m}\hspace{2pt}\)倍(mは整数)であるため、以下のようになります。 $$\large{2d = m\lambda}$$ 間隔\(\hspace{2pt}\large{d}\hspace{2pt}\)に(1)式の結果を代入すると、以下の式が求められます。
\(\hspace{2pt}\large{\displaystyle x = \sqrt{m R \lambda} \hspace{10pt} (m=0,1,2,\cdots)}\hspace{2pt}\)
【2】ニュートンリングの応用例(曲率半径の測定)
ニュートンリングの応用例として、ニュートン原器による曲率半径Rの測定があります。
前章で解説した平板ガラスと球面レンズのニュートンリングでも曲率半径を測定できますが、測定できる曲率半径はほとんど平面に近い球面レンズ面のみに限られます。
(なぜ、平板と球面の組み合わせで測定が困難となるかの理由は後述しています。(【3-3】ニュートンリングの縞の間隔))
そこで、球面レンズの製造現場で実用的に用いられている測定として、図2のように曲率半径Rを測定したい被検レンズと、曲率半径Rの基準となるニュートン原器を重ね合わせる方法が取られています。
このような測定方法を取ることで、被検レンズの曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)と、基準となるニュートン原器の曲率半径\(\hspace{2pt}\large{R_0}\hspace{2pt}\)との差分が干渉縞として現れることになります。
ニュートン原器との差分を観察することで、曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)の小さい球面レンズでも測定を行うことができます。
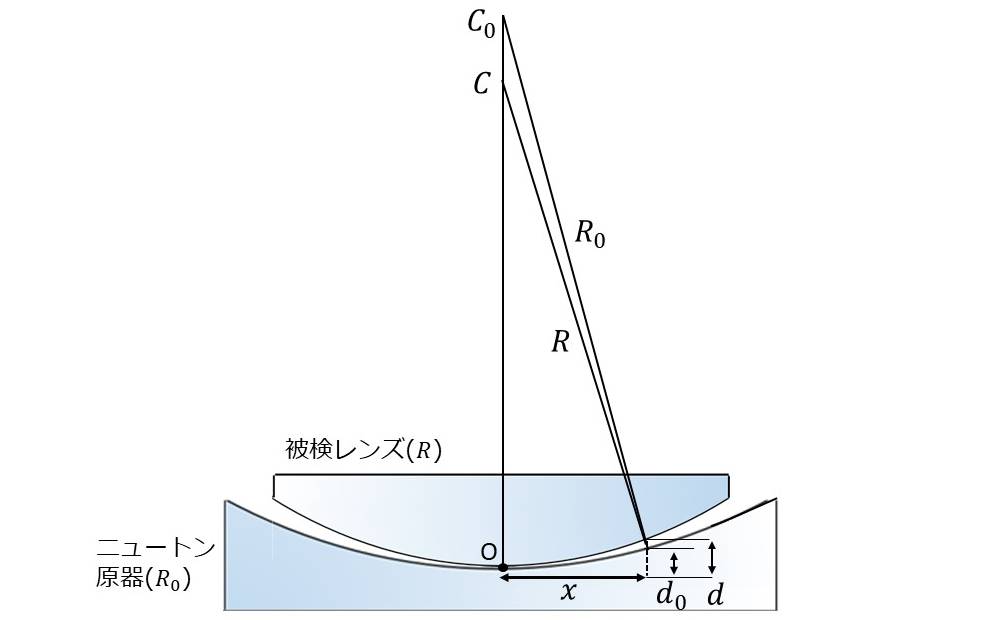
図4のように、曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)の被検レンズと、基準となる曲率半径\(\hspace{2pt}\large{R_0}\hspace{2pt}\)のニュートン原器の2つのレンズを重ね合わせた場合を考えます。
前章の計算結果から、位置\(\hspace{2pt}\large{x}\hspace{2pt}\)における2枚のレンズの接点\(\hspace{2pt}\large{O}\hspace{2pt}\)からの曲面までの高さ\(\hspace{2pt}\large{d,d_0}\hspace{2pt}\)は、以下のようになります。 $$\large{d \approx \frac{x^2}{2R}}$$ $$\large{d_0 \approx \frac{x^2}{2R_0}}$$
このとき、明るい縞の発生する条件を求めると、以下のようになります。 $$\large{2(d - d_0) = \frac{1}{2}(2m+1) \lambda}$$ 高さ\(\hspace{2pt}\large{d,d_0}\hspace{2pt}\)を代入すると以下の式が得られます。 $$\large{x^2(\frac{1}{R} - \frac{1}{R_0}) = \frac{1}{2}(2m+1) \lambda}$$
\(\hspace{2pt}\large{\displaystyle x^2\left(\frac{1}{R} - \frac{1}{R_0}\right) = \frac{1}{2}(2m+1) \lambda \hspace{10pt}}\hspace{2pt}\)\(\hspace{2pt}\large{(m=0,1,2,\cdots)}\hspace{2pt}\)
また、暗い縞が発生する条件も同様に求められます。
\(\hspace{2pt}\large{\displaystyle x^2\left(\frac{1}{R} - \frac{1}{R_0}\right) = m \lambda \hspace{10pt} (m=0,1,2,\cdots)}\hspace{2pt}\)
上記の計算結果から、レンズの中心から\(\hspace{2pt}\large{x}\hspace{2pt}\)の位置に\(\hspace{2pt}\large{m}\hspace{2pt}\)番目の暗い縞が観測されたとすると、被検レンズの曲率は以下のように求められます。 $$\large{\displaystyle R = \frac{R_0 x^2}{m \lambda R_0 + x^2}}$$
【3】ニュートンリングの計算問題
本章では、ニュートンリングに関連した計算問題を解説します。
【3-1】曲率半径Rの計算
【問題】
図1の実験系(球面ガラス面と平板ガラス)において、620nmの赤色の光を入射し、上方からニュートンリングを観察した。
ちょうど中心から\(\hspace{2pt}\large{x=5.0[mm]}\hspace{2pt}\)の位置に10番目の暗い縞を観測した場合、曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)を計算せよ。
【回答と解説】
暗い縞の発生条件は、 $$\large{\displaystyle x = \sqrt{m R \lambda}}$$ であるので、暗い縞の観測された条件を代入し、曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)を求めます。 $$\large{\displaystyle R = \frac{x^2}{m \lambda} = \frac{{0.005}^{2}}{10 \times 620 \times 10^{-9}}=4.0[m]}$$ したがって、 $$\large{R=4000[mm]}$$
【3-2】ニュートン原器による曲率半径Rの計算
【問題】
図3の実験系(披検レンズ面(凸面)とニュートン原器(凹面))において、被検レンズ面側から620nmの赤色の光を入射し、その反射光からニュートンリングを観察した。
ニュートン原器の曲率半径\(\hspace{2pt}\large{R_0=100[mm]}\hspace{2pt}\)であるとき、ちょうど中心から\(\hspace{2pt}\large{x=5.0[mm]}\hspace{2pt}\)の位置に4番目の暗い縞を観測した場合、被検レンズの曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)を計算せよ。(図3のように曲率半径は\(\hspace{2pt}\large{R < R_0}\hspace{2pt}\)であるとする。)
【回答と解説】
暗い縞の発生条件は、 $$\large{\displaystyle x^2\left(\frac{1}{R} - \frac{1}{R_0}\right) = m \lambda}$$ であることから、暗い縞の観測された条件を代入し、曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)を求めます。 \begin{eqnarray} \large \frac{1}{R} &\large =&\large \frac{m \lambda}{x^2} +\frac{1}{R_0}\\[0.7em] \large &\large =&\large \frac{4 \times 620 \times 10^{-9}}{0.005^2} +\frac{1}{0.1}\\[0.7em] \large &\large =&\large 10.099 \cdots\\[0.7em] \end{eqnarray} したがって、 $$\large{R=99[mm]}$$
【3-3】ニュートンリングの縞の間隔
【問題】
図1の実験系 (球面ガラス面と平板ガラス) において、620nmの赤色の光を入射し、上方からニュートンリングを観察した。
曲率半径\(\hspace{2pt}\large{R=100}\hspace{2pt}\)[mm]の球面ガラス面を観測ときのニュートンリングの縞の間隔を計算し、『なぜ球面の曲率半径が小さい場合は "球面ガラス面" と "平板ガラス" の組み合わせが曲率半径の測定に適さないか』を考察せよ。
【回答と解説】
暗い縞の発生条件は、 $$\large{\displaystyle x = \sqrt{m R \lambda}}$$ であり、ニュートンリングの縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)は、m+1番目とm番目の縞の位置の差分から計算されます。 $$\large{\Delta x} = \sqrt{(m+1) R \lambda} - \sqrt{m R \lambda}$$
例えば、曲率半径\(\hspace{2pt}\large{R=100}\hspace{2pt}\)[mm] のときの、0番目から1番目の暗線の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)を求めると、以下のように計算されます。 \begin{eqnarray} \large \Delta x &\large =&\large \sqrt{1 \times 100 \times 10^{(-3)} \times 620 \times 10^{(-9)}}\\[0.7em] \large &\large =&\large 0.25[mm]\\[0.7em] \end{eqnarray}
同様に、0番目から5番目までの縞の間隔を計算した結果を以下の表に示します。
| m番目 | m+1番目 | 縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\) |
|---|---|---|
| 0 | 1 | 0.25mm |
| 1 | 2 | 0.1mm |
| 2 | 3 | 0.1mm |
| 3 | 4 | 0.07mm |
| 4 | 5 | 0.06mm |
縞の間隔が最も広い0番目と1番目間隔でも0.25mmでしかなく、次の縞の間隔では0.1mmまで狭くなってしまいます。あまりに縞の間隔が狭すぎるため、縞の本数や位置の特定が困難となり、測定には適しません。
このような理由で、曲率半径の小さい面の場合は、第2章で説明したニュートン原器を使用し、原器との差分の干渉縞を観測します。