マイケルソン干渉計とは
本項では、マイケルソン干渉計の原理や明暗の条件、計算例について解説します。
【1】マイケルソン干渉計とは
マイケルソン干渉計(Michelson interferometer)は、アルバート・マイケルソンによって1880年に開発され、現代でも標準的な干渉計の構成として知られています。
マイケルソン干渉計は、光源から照射された光をハーフミラーにより2つの経路に分割し、各経路のミラーで反射させることで再度重ね合わせ、干渉縞を作り出します。
この干渉縞を観測することで、光の経路のわずかな長さの変化や、光の経路に挿入された物質の屈折率の測定に活用されます。
【1-1】マイケルソン干渉計の構成
マイケルソン干渉計は、図1に示す構成が基本となります。
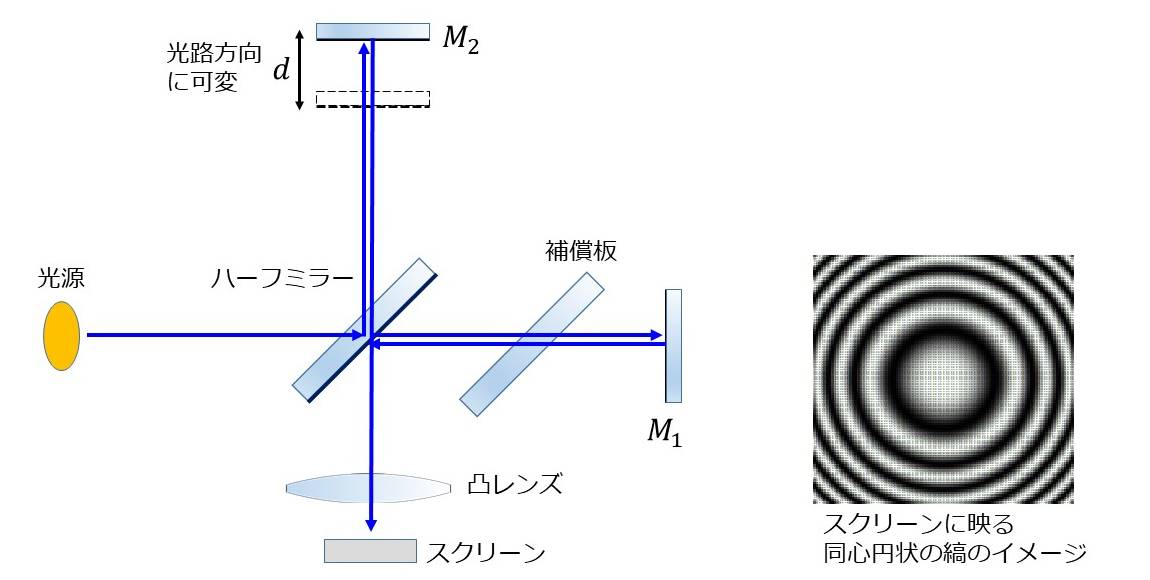
射出する光線が広がりを持つ光源から照射された光を、ハーフミラー(半透明鏡)によって2つの経路に分割します。
分割された光はそれぞれミラー\(\hspace{2pt}\large{M_1, M_2}\hspace{2pt}\)により反射され、再びハーフミラーに戻ります。
ミラー\(\hspace{2pt}\large{M_1}\hspace{2pt}\)から反射された光の一部がハーフミラーにより反射されスクリーンに向かいます。また、\(\hspace{2pt}\large{M_2}\hspace{2pt}\)から反射された光の一部が透過し、スクリーンに向かいます。
\(\hspace{2pt}\large{M_1,M_2}\hspace{2pt}\)の2つの経路からの光をスクリーンの前のレンズによって集光し、干渉縞を映し出します。干渉縞は図1(右側)のように同心円状の縞が形成されます。
図1では、スクリーンに干渉縞を映し出し観測をする実験系を描いていますが、測定によっては縞の変化を人の目で観察することが困難な場合があります。
その場合は、スクリーンの代わりに、電子的に光の強度の変化を測定する測定器が使用されることもあります。
【1-2】補償板
ハーフミラーとミラー\(\hspace{2pt}\large{M_1}\hspace{2pt}\)の間には、補償板が置かれます。
補償板は、ハーフミラーと同じ厚みで作られており、ハーフミラーと平行に設置します。
この補償板を設置する理由は、分割された光同士の光路長を一致させるためです。
ミラー\(\hspace{2pt}\large{M_1}\hspace{2pt}\)により反射される光の経路では、ハーフミラーのガラスを1回だけ透過します。
一方、ミラー\(\hspace{2pt}\large{M_2}\hspace{2pt}\)により反射される光の経路では、ハーフミラーのガラスを計3回透過することになります。
補償板を入れることで、ミラー\(\hspace{2pt}\large{M_1}\hspace{2pt}\)により反射される経路でも、計3回ガラスを透過することになり、光路長を一致させることができます。
特に、白色光を使用する場合には、波長の分散が発生し干渉縞が不鮮明になるため、補償板が必要となります。
なお、キューブ型のビームスプリッターを使用した場合は、反射と透過で光路長が等しいため、補償板は使用しません。
【1-3】同心円の干渉縞が発生する原理
マイケルソン干渉計の干渉縞が同心円の縞となる理由は、縞の発生位置が光源から射出される光線の角度に依存しているためです。
マイケルソン干渉計では、射出する光線が広がりを持った光源を使用します。(もしくは、レーザー光線を対物レンズなどで拡散して光源とする場合もあります。)
ここで、図2のように、光源面のうち軸から距離Lの位置の点光源に着目し、この点光源から角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)で射出される光線の光路長差を計算します。
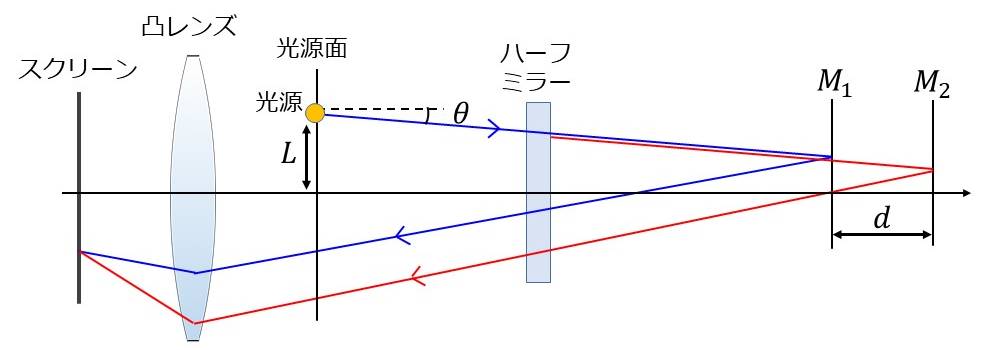
ハーフミラーにより分割された光は、異なる経路に分割されますが、図2では差分を分かりやすくするために同一の平面に描いています。また、ハーフミラーに到達した後、光源とは別の方向に進行しますが、1つの平面で表現するため、光源とスクリーンを並べて描いています。
図2より、角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)で射出された光は、ハーフミラーで分割された後、ミラー\(\hspace{2pt}\large{M_1,M_2}\hspace{2pt}\)それぞれに反射角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)で入射します。
ここで、図3にミラー\(\hspace{2pt}\large{M_2}\hspace{2pt}\)での反射の様子を拡大した図を示します。
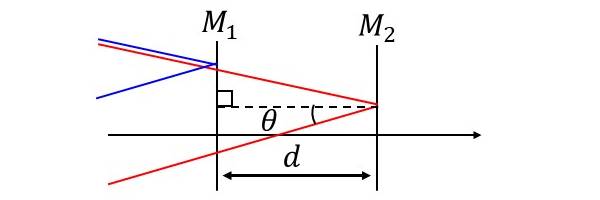
図3に示されているように、光路長差は『角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)』と『\(\hspace{2pt}\large{M_1}\hspace{2pt}\)と\(\hspace{2pt}\large{M_2}\hspace{2pt}\)の光路長差\(\hspace{2pt}\large{d}\hspace{2pt}\)』により決まることが分かります。
光路長差を計算すると、以下のようになります。
$$\large{\rm{(光路長差)} = 2d \cos \theta}$$
ミラー\(\hspace{2pt}\large{M_1,M_2}\hspace{2pt}\)による光路長差\(\hspace{2pt}\large{d}\hspace{2pt}\)を一定とすれば、光線の角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)に依存して縞の明暗が決まります。
角度\(\hspace{2pt}\large{\theta=0}\hspace{2pt}\)の場合は、スクリーンの中心で光が重なり合います。また、角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)が大きいほど、外側に縞が形成されることになります。
また、光源面の軸から距離\(\hspace{2pt}\large{L}\hspace{2pt}\)の点光源は円状に存在しているため、同じ光路長差の条件を満たした縞が円状に形成されることになります。
その結果、外側ほど角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)の大きい光路長差の条件で干渉する、同心円の縞がスクリーン上に観測されることになります。
【1-4】干渉縞の明暗の条件
干渉縞の明暗の条件について考えます。
前章の計算から、光路長差は以下のようになります。 $$\large{\rm{(光路長差)} = 2d \cos \theta}$$
ここで、ミラー\(\hspace{2pt}\large{M_1}\hspace{2pt}\)の経路では、ミラー\(\hspace{2pt}\large{M_1}\hspace{2pt}\)とハーフミラーによる反射によって、2度位相の跳びが発生します。一方、ミラー\(\hspace{2pt}\large{M_2}\hspace{2pt}\)の経路では、ミラー\(\hspace{2pt}\large{M_2}\hspace{2pt}\)での反射のみで位相の跳びが発生します。
したがって、2つの経路での位相の跳びを合計すると、\(\hspace{2pt}\large{\pi}\hspace{2pt}\)だけ位相の変化を考慮すればよいことになります。
したがって、強め合う条件は以下のようになります。
\(\hspace{2pt}\large{\displaystyle 2d \cos \theta = \frac{1}{2}(2m +1) \lambda\hspace{10pt} (\rm{mは整数})}\hspace{2pt}\)
また、弱め合う干渉が発生する条件は以下のようになります。
\(\hspace{2pt}\large{\displaystyle 2d \cos \theta = m \lambda\hspace{10pt} (\rm{mは整数})}\hspace{2pt}\)
【2】マイケルソン干渉計の応用例
マイケルソン干渉計は、2つに分割された経路の光路長の変化によって、干渉の条件が変化します。
したがって、干渉縞の変化を観察することで、2つに分割された経路の光路長の変化を読み取ることができます。
スクリーン上の同心円の干渉縞の『明』→『暗』→『明』(もしくは『暗』→『明』→『暗』)の変化を、縞1本分の変化を観測したと定義します。このとき、縞1本分の変化に対応する光路長差は\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)に相当します。
縞の変化した数を\(\hspace{2pt}\large{N}\hspace{2pt}\)とすると、光路長の差分\(\hspace{2pt}\large{2 \Delta d}\hspace{2pt}\)との関係は以下のようになります。(ハーフミラーからミラーまでの経路での変化を\(\hspace{2pt}\large{\Delta d}\hspace{2pt}\)、往復分を考慮し\(\hspace{2pt}\large{2\Delta d}\hspace{2pt}\)としています。) $$\large{2 \Delta d = N \lambda}$$
したがって、光路長の変化\(\hspace{2pt}\large{\Delta d}\hspace{2pt}\)は以下のようになります。
\(\hspace{2pt}\large{\displaystyle \Delta d = N \frac{\lambda}{2}\hspace{10pt}(1)}\hspace{2pt}\)
【2-1】光源波長の測定
マイケルソン干渉計の応用の1つに、光源波長の測定があります。
(1)式の光路長と縞の変化の関係より、マイケルソン干渉計の片方のミラーを移動させることで発生する光路長差\(\hspace{2pt}\large{\Delta d}\hspace{2pt}\)が既知であれば、縞の変化から光源波長の長さを求めることができます。 $$\large{\lambda = \frac{2 \Delta d}{N}}$$
空気の屈折率も考慮する場合、真空中の波長\(\hspace{2pt}\large{\lambda_{0}}\hspace{2pt}\)と空気中の波長\(\hspace{2pt}\large{\lambda_{air}}\hspace{2pt}\)、空気の屈折率\(\hspace{2pt}\large{n_{air}}\hspace{2pt}\)の関係が、\(\hspace{2pt}\large{\lambda_{air} = \frac{1}{n_{air}}\lambda_{0}}\hspace{2pt}\)であることから、以下のようになります。 $$\large{\lambda_0 = \frac{2 n_{air} \Delta d }{N}}$$
【2-2】気体の屈折率の測定
図4のように、マイケルソン干渉計の経路の片方に真空チャンバーを設置することで、気体の屈折率を測定できます。
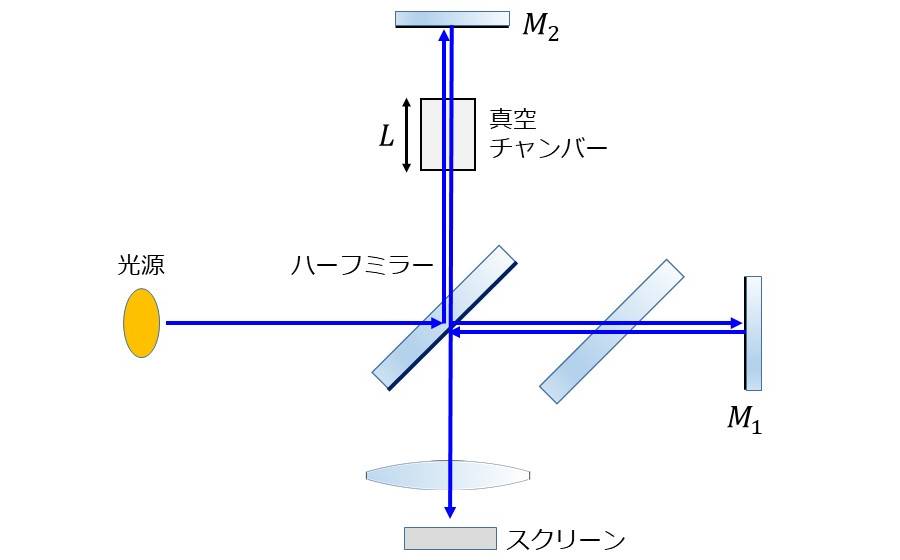
真空チャンバーの光路に沿った長さが\(\hspace{2pt}\large{L}\hspace{2pt}\)とすると、真空を伝搬する光路長\(\hspace{2pt}\large{2 d_0}\hspace{2pt}\)は以下となります。 $$\large{2d_0 = 2 L }$$
また、真空チャンバーに屈折率\(\hspace{2pt}\large{n_{gas}}\hspace{2pt}\)の気体を注入したとき、気体中を伝搬する光路長\(\hspace{2pt}\large{2d_{gas}}\hspace{2pt}\)は以下となります。 $$\large{2d_{gas} = 2nL}$$
したがって、屈折率\(\hspace{2pt}\large{n_{gas}}\hspace{2pt}\)の気体を入れた場合と真空を入れた場合の光路長差\(\hspace{2pt}\large{2 \Delta d}\hspace{2pt}\)は以下となります。 $$\large{2 \Delta d =2d_{gas}-2d_0 =2n_{gas}L - 2L}$$
(1)式の光路長と縞の変化の関係より、気体の屈折率\(\hspace{2pt}\large{n_{gas}}\hspace{2pt}\)を求めることができます。 $$\large{2n_{gas}L - 2L = N \lambda}$$ $$\large{n_{gas} = 1+\frac{\lambda}{2L}N}$$
【3】マイケルソン干渉計の計算問題
本章では、マイケルソン干渉計に関連した計算問題を解説します。
【3-1】空気の屈折率の計算問題
【問題】
前章の図4のように、マイケルソン干渉計の分割された経路の片方に真空チャンバーを設置し、真空の状態で干渉縞を観測した。
その状態から、真空チャンバーに空気を徐々に入れ明暗の縞の変化する回数\(\hspace{2pt}\large{N}\hspace{2pt}\)を計測した。
測定波長\(\hspace{2pt}\large{\lambda = 589.3[nm]}\hspace{2pt}\)、真空チャンバーの長さ\(\hspace{2pt}\large{L=5[cm]}\hspace{2pt}\)、観測された縞の変化が\(\hspace{2pt}\large{N=47}\hspace{2pt}\)であったとき、空気の屈折率\(\hspace{2pt}\large{n_{air}}\hspace{2pt}\)を求めよ。
【解答と解説】
前章の気体の屈折率の公式に当てはめて計算を行います。気体の屈折率\(\hspace{2pt}\large{n_{gas}}\hspace{2pt}\)は以下の式により計算されます。
$$\large{n_{gas} = 1+\frac{\lambda}{2L}N}$$
与えられた条件を代入し空気の屈折率\(\hspace{2pt}\large{n_{air}}\hspace{2pt}\)を求めると、以下のようになります。 $$\large{n_{gas} = 1+\frac{598.2 \times 10^{-9}}{2 \times 5 \times 10^{-2}} 47 \approx 1.000277}$$
参考文献
(1)Eugene Heght『原著5版 ヘクト 光学Ⅱ』 令和元年6月15日発行.pp232~237