ヤングの実験とは
本項では以下の内容を解説しています。
- ・ヤングの実験の原理
- ・干渉縞の公式の導出
- ・縞間隔の計算
- ・光路長が変化したときの縞の位置の計算
【1】ヤングの実験とは
ヤングの実験とは、光源をスリットにより分割し、それぞれのスリットからの光が重なる様子を、スクリーン上で観測する実験のことです。
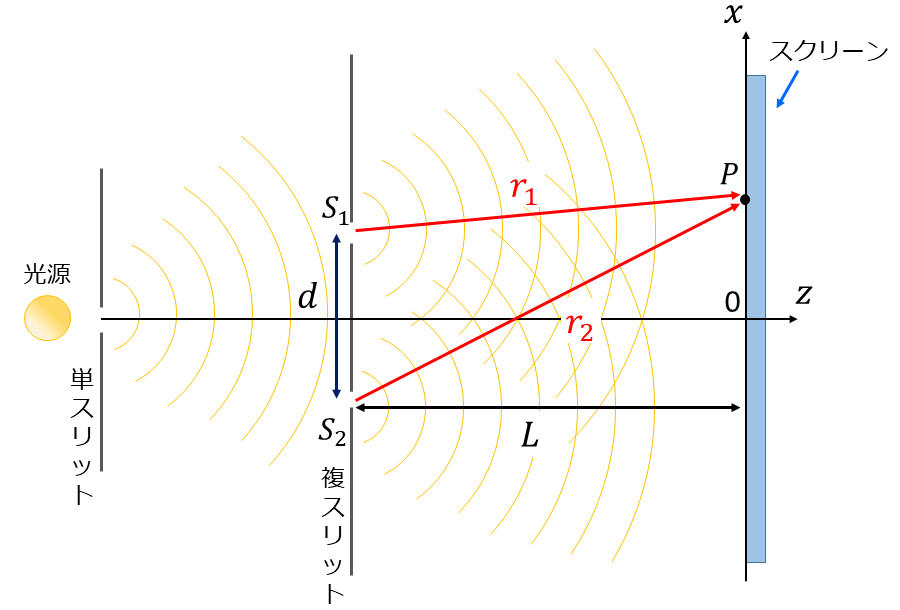
図1にヤングの実験の概略図を示します。
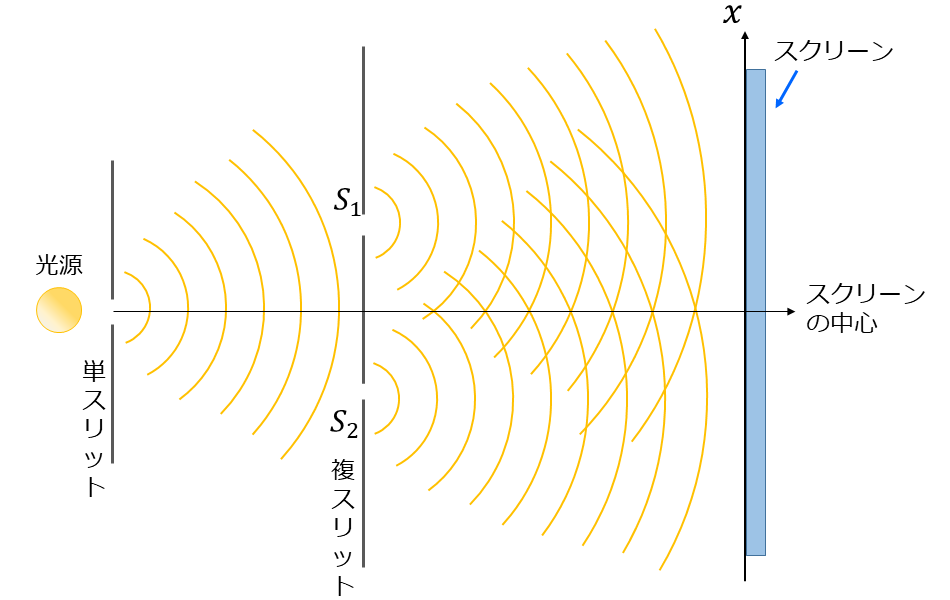
図1に示されているように、ヤングの実験では光源からの光を単スリットに入射し、さらに2つのスリット\(\hspace{2pt}\large{S_1}\hspace{2pt}\)、\(\hspace{2pt}\large{S_2}\hspace{2pt}\)で光を分割しています。
各スリットに到達した光は球面状に広がり、2つのスリットからの光がスクリーン上で重なり合います。
スクリーン上で重なった光は、明暗が繰り返される干渉縞を発生させます。図2にスクリーン上に発生する干渉縞のイメージを示します。
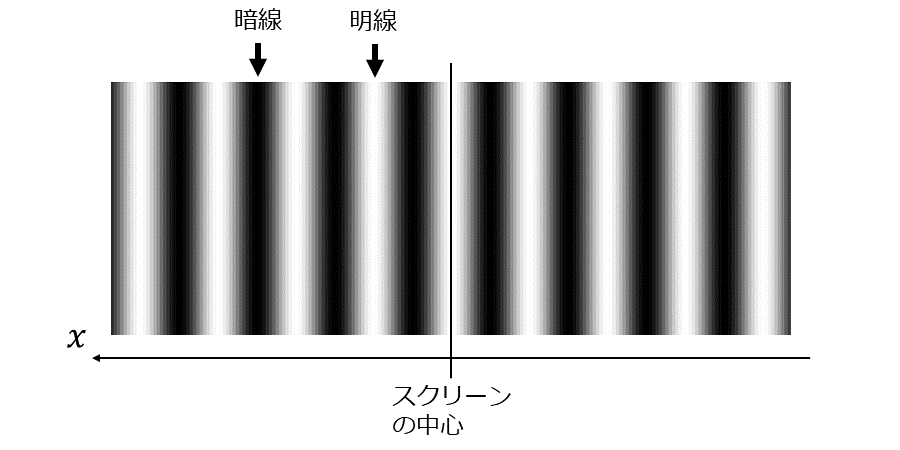
図2では、色によって光強度の強弱を示しており、白色が光強度が大きい箇所(明線)、黒色が光強度が小さい箇所(暗線)を表しています。
スクリーンの中心には明線が位置し、中心から対称的に干渉縞が発生するという特徴があります。
(本来は、スクリーンの中心から離れるほど、光が球面に広がる影響により光強度は低下します。図2はスクリーンの中心の近傍で、光強度の低下がないと近似して計算した結果を示しています。)
【2】干渉縞の明暗の条件の導出
スクリーン上で観測される干渉縞の明暗の条件を導出します。
図3のように、複スリットの間隔を\(\hspace{2pt}\large{d}\hspace{2pt}\)、複スリットからスクリーンまでの距離を\(\hspace{2pt}\large{L}\hspace{2pt}\)とします。
また、スリット\(\hspace{2pt}\large{S_1}\hspace{2pt}\)とスリット\(\hspace{2pt}\large{S_2}\hspace{2pt}\)から放射された光がスクリーン上の点Pで重なったとき、各スリットから点Pまでの距離を\(\hspace{2pt}\large{r_1}\hspace{2pt}\)、\(\hspace{2pt}\large{r_2}\hspace{2pt}\)とします。
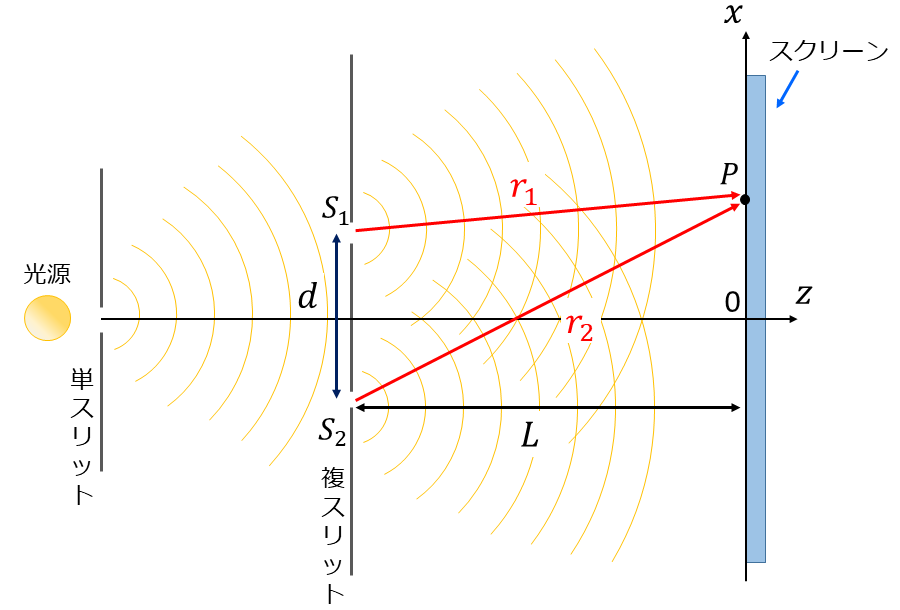
ヤングの実験では、スリット\(\hspace{2pt}\large{S_1}\hspace{2pt}\)と\(\hspace{2pt}\large{S_2}\hspace{2pt}\)からの光が異なる長さの経路で伝搬することにより、点Pの位置で位相差が発生し、干渉が出現します。
このとき、スクリーン上の点Pにおける光路差は\(\hspace{2pt}\large{r_2-r_1}\hspace{2pt}\)により計算されます。
【2-1】光路差の計算
スクリーン上の点Pにおける光路差(\(\hspace{2pt}\large{r_2 - r_1}\hspace{2pt}\))を位置\(\hspace{2pt}\large{x}\hspace{2pt}\)の関数として導出します。
\(\hspace{2pt}\large{r_1}\hspace{2pt}\)、\(\hspace{2pt}\large{r_2}\hspace{2pt}\)は図3より以下の式で表されます。 $$\large{r_1 = \sqrt{{L}^2+{\left(x-\frac{d}{2}\right)}^2}}$$ $$\large{r_2 = \sqrt{{L}^2+{\left(x+\frac{d}{2}\right)}^2}}$$
ここで、複スリットからスクリーンまでの距離\(\hspace{2pt}\large{L}\hspace{2pt}\)が、スリット間隔\(\hspace{2pt}\large{d}\hspace{2pt}\)よりも十分に大きいとすると、以下にように近似することができます。 \begin{eqnarray} \large r_1&\large =&\large \sqrt{{L}^2+{\left(x-\frac{d}{2}\right)}^2}\\[0.7em] &\large =&\large L \sqrt{1+\left(\frac{x-\frac{d}{2}}{L}\right)^2 }\\[0.7em] &\large \approx& \large L \left( 1+\frac{1}{2} \frac{{\left(x - \frac{d}{2}\right)}^2}{{L}^2} \right)\\[0.7em] &\large =&\large L + \frac{1}{2} \frac{{\left(x - \frac{d}{2}\right)}^2}{L} \end{eqnarray}
\(\hspace{2pt}\large{r_2}\hspace{2pt}\)についても同様の近似が成り立つので、以下のようになります。 $$\large{r_2 \approx L + \frac{1}{2} \frac{{(x + \frac{d}{2})}^2}{L}}$$ したがって、光路差\(\hspace{2pt}\large{r_2 - r_1}\hspace{2pt}\)を計算すると以下となります。 $$\large{r_2 - r_1 \approx \frac{d}{L}x}$$
【2-2】明線の発生する条件
まず、スクリーン上に明線の発生する条件を求めます。
明線は、光路差が波長の整数倍に等しい場合に発生します。
したがって、整数\(\hspace{2pt}\large{m}\hspace{2pt}\)における縞の位置を\(\hspace{2pt}\large{x_m}\hspace{2pt}\)としたときの、明線が発生する条件は以下となります。
$$\large {\frac{d}{L}x_m = m \lambda} $$ $$ \large (m=0\hspace{1pt},\hspace{1pt}\pm1\hspace{1pt},\hspace{1pt}\pm2\hspace{1pt},\hspace{1pt}\cdots)$$
また、上式から明縞が発生するスクリーン上の座標\(\hspace{2pt}\large{x_m}\hspace{2pt}\)は以下のようになります。 $$\large{x_m=0,\ \pm \frac{L}{d}\lambda,\ \pm \frac{2L}{d}\lambda, \cdots}$$
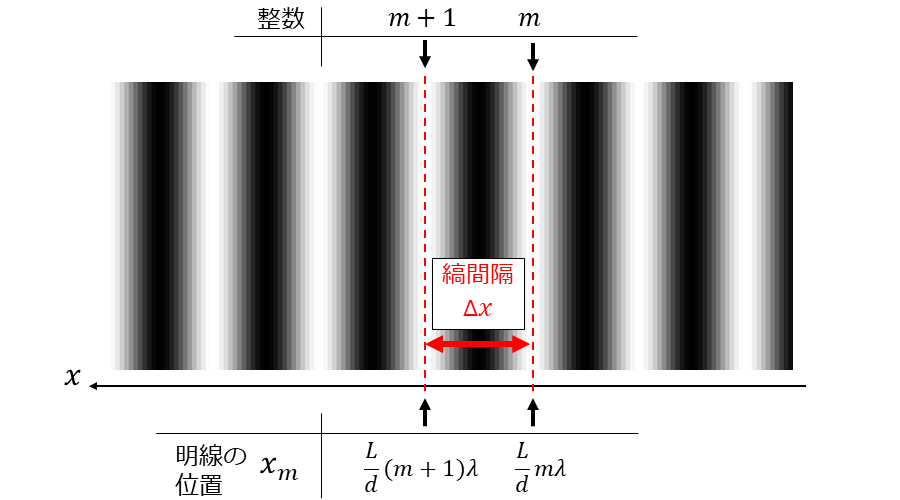
図4にスクリーン上に発生する縞の明線の整数\(\hspace{2pt}\large{m}\hspace{2pt}\)と、縞の発生位置\(\hspace{2pt}\large{x_m}\hspace{2pt}\)の関係を図示します。
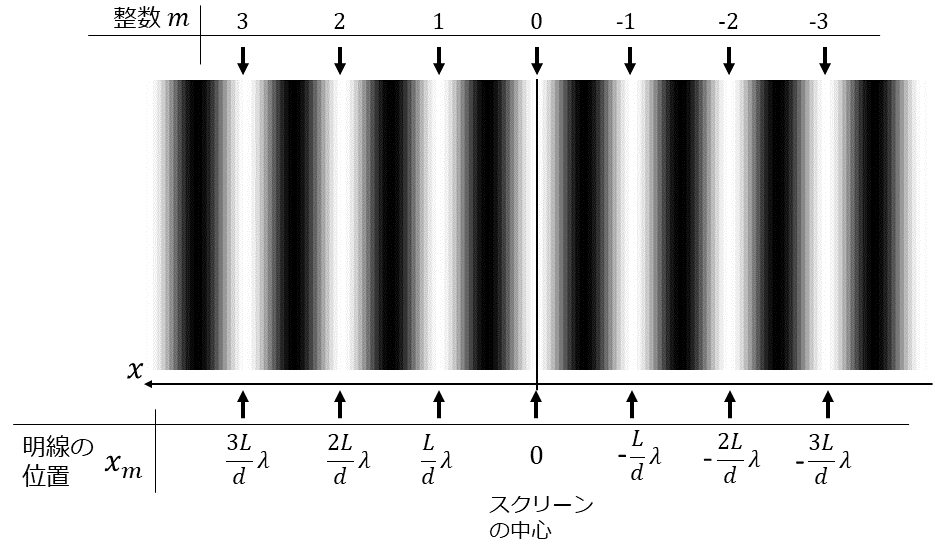
図4のように、スクリーンの中心には整数\(\hspace{2pt}\large{m=0}\hspace{2pt}\)に相当する明線が発生します。スクリーンの中心に明線が発生する理由は、スクリーンの中心ではスリット\(\hspace{2pt}\large{S_1}\hspace{2pt}\)、\(\hspace{2pt}\large{S_2}\hspace{2pt}\)から点Pまでの距離が等しくなるため(\(\hspace{2pt}\large{r_1 = r_2}\hspace{2pt}\))、光の位相が一致し、強め合う干渉となります。
また、その\(\hspace{2pt}\large{m=0}\hspace{2pt}\)の明線を中心にして、整数\(\hspace{2pt}\large{m}\hspace{2pt}\)の大きい縞が順番にスクリーンに映し出されます。
【2-2】暗線の発生する条件
縞が暗くなるためには、光路差が波長の長さの\(\hspace{2pt}\large{\frac{1}{2}(2m+1)}\hspace{2pt}\)倍(\(\hspace{2pt}\large{m}\hspace{2pt}\)は整数)である必要があります。 したがって、縞が暗くなるときの光路長差は以下となります。 $$\large{r_2 - r_1 = \frac{1}{2}(2m+1)\lambda}$$
縞が明るくなるときの計算結果をそのまま使うと、暗線の発生する条件は以下のようになります。
$$\large \frac{d}{L}x_m = \frac{1}{2}(2m+1)\lambda $$ $$\large (m=0\hspace{1pt},\hspace{1pt}\pm1\hspace{1pt},\hspace{1pt}\pm2\hspace{1pt},\hspace{1pt}\cdots)$$
【3】ヤングの実験の計算問題
本章では、ヤングの実験に関連した計算問題を記載します。
【3-1】干渉縞の間隔の計算問題
【問題】
図5の実験系において、明線の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)の一般式を求めよ。
また、\(\hspace{2pt}\large{d=0.5[mm]}\hspace{2pt}\)、\(\hspace{2pt}\large{L=1[m]}\hspace{2pt}\)であるとき、明線の間隔が\(\hspace{2pt}\large{\Delta x = 1.26[mm]}\hspace{2pt}\)であった。光源の光の波長\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)を求めよ。
【回答と解説】
まず、干渉縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)を計算します。
干渉縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)は、ある整数\(\hspace{2pt}\large{m}\hspace{2pt}\)における明線と、\(\hspace{2pt}\large{m+1}\hspace{2pt}\)における明線の位置の差分を求めることで計算します。
整数\(\hspace{2pt}\large{m}\hspace{2pt}\)の明線の発生条件は以下のようになります。 $$\large{ \displaystyle \frac{d}{L}x = m \lambda \hspace{10pt} (1)}$$ また、整数\(\hspace{2pt}\large{m+1}\hspace{2pt}\)の縞の条件は、以下の通りです。 $$\large{\displaystyle \frac{d}{L}(x + \Delta x) = (m+1) \lambda \hspace{10pt} (2)}$$ (1)式と(2)式の両辺の差分を計算すると、縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)は $$\large{\Delta x = \frac{L \lambda}{d}}$$
下の図に、整数\(\hspace{2pt}\large{m}\hspace{2pt}\)と\(\hspace{2pt}\large{m+1}\hspace{2pt}\)の縞の位置と縞間隔の関係を図示した図を示します。
また、求められた縞間隔の式\(\displaystyle\hspace{2pt}\large{\Delta x = \frac{L \lambda}{d}}\hspace{2pt}\)から\(\hspace{2pt}\large{\Delta x = 1.26[mm]}\hspace{2pt}\)のときの光源の波長は以下のように求められます。 \begin{eqnarray} \large \hspace{10pt} \lambda &\large =&\large \frac{d \Delta x}{L} \hspace{10pt}\\[0.5em] &\large =&\large \frac{0.5 \times 10^{-3} \times 1.26 \times 10^{-3}}{1}\\[0.5em] &\large =&\large 6.30 \times 10^{-7}[m]\\[0.5em] \end{eqnarray}
【3-2】光路長を変化させた場合の計算問題
【問題】
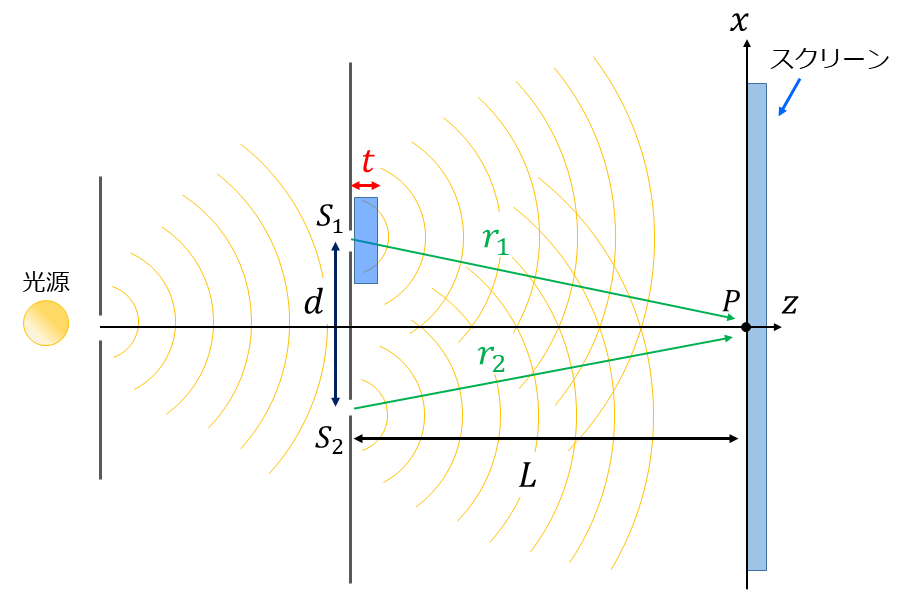
スリット\(\hspace{2pt}\large{s_1}\hspace{2pt}\)のスクリーン側に屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)、厚み\(\hspace{2pt}\large{t}\hspace{2pt}\)の透明媒質を配置したとき、スクリーンの中心(\(\hspace{2pt}\large{x=0}\hspace{2pt}\))の位置にあった干渉縞の位置はどれだけ変化するか。
(ただし、厚み\(\hspace{2pt}\large{t}\hspace{2pt}\)は、複スリットからスクリーンまでの距離\(\hspace{2pt}\large{L}\hspace{2pt}\)に比べて十分に薄く、透明媒質中を光は\(\hspace{2pt}\large{z}\hspace{2pt}\)軸方向に平行に進行するとして計算する。)
【回答と解説】
問題文の『スクリーンの中心で発生していた明線』は、整数\(\hspace{2pt}\large{m=0}\hspace{2pt}\)において強め合う縞のことです。 したがって、\(\hspace{2pt}\large{m=0}\hspace{2pt}\)の条件で発生した明線がどれだけ\(\hspace{2pt}\large{x}\hspace{2pt}\)方向にずれるかを計算します。
スリット\(\hspace{2pt}\large{S_1}\hspace{2pt}\)の前に屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)の透明媒質を配置したときの光路長は以下のようになります。 $$\large{r_1 = S_1 P -t + nt}$$ 光路差を計算すると以下のようになります。
したがって、上記の光路差に対して明線の発生する条件は、以下のようになります。 $$\large{\frac{d}{L}x +t -nt = m \lambda}$$ スクリーンの中心に発生していた明縞は、整数\(\hspace{2pt}\large{m=0}\hspace{2pt}\)の条件で発生していたため、\(\hspace{2pt}\large{m=0}\hspace{2pt}\)を上式に代入すると、 $$\large{\frac{d}{L}x +t -nt = 0}$$ $$\large{x = \frac{(n-1)tL}{d}}$$ したがって、スリット\(\hspace{2pt}\large{s_1}\hspace{2pt}\)のスクリーン側に屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)、厚み\(\hspace{2pt}\large{t}\hspace{2pt}\)の透明媒質を配置すると、\(\hspace{2pt}\large{m=0}\hspace{2pt}\)の明線は\(\displaystyle\hspace{2pt}\large{\frac{(n-1)tL}{d}}\hspace{2pt}\)だけ上方の位置に変化します。