エバネッセント波

本項では、以下の内容について解説します。

• ・エバネッセント波とは
• ・染み出し深さを表す数式
• ・エバネッセント波の計算例

【1】全反射とエバネッセント波

エバネッセント波とは、媒質の境界面で全反射が発生したときに、反射と反対方向に電磁場が染み出る現象のことをいいます。

本章では、光の全反射の条件とエバネッセント波の概要について解説します。

【1-1】光の全反射の条件

異なる屈折率の媒質の境界に光が入射すると、図1左のように、透過光と反射光に分かれて伝搬します。

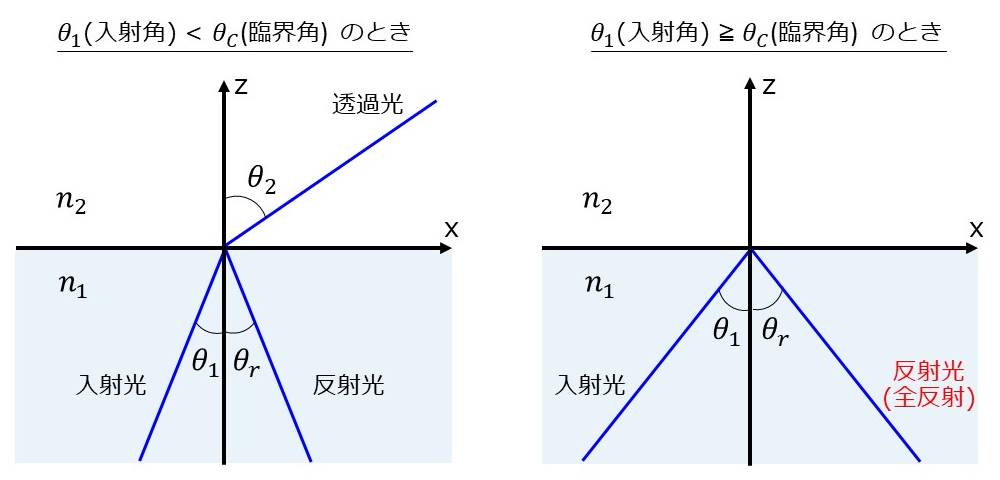
入射側の媒質の屈折率が\(\hspace{2pt}\large{n_1}\hspace{2pt}\)、透過側の屈折率が\(\hspace{2pt}\large{n_2}\hspace{2pt}\)であるとき、入射角\(\hspace{2pt}\large{\theta_1}\hspace{2pt}\)と屈折角\(\hspace{2pt}\large{\theta_2}\hspace{2pt}\)の間に以下のスネルの法則が成り立ちます。 $$\large{\frac{n_2}{n_1}=\frac{\sin \theta_1}{\sin \theta_2}}$$

上式において、屈折角\(\hspace{2pt}\large{\theta_2}\hspace{2pt}\)が\(\hspace{2pt}\large{90°}\hspace{2pt}\)となるような入射角度を臨界角\(\hspace{2pt}\large{\theta_c}\hspace{2pt}\)といいます。

臨界角\(\hspace{2pt}\large{\theta_c}\hspace{2pt}\)より大きい入射角度の光では、透過側に光が伝搬せず、図1右のように全エネルギーが反射されます。 このような現象を全反射といいます。

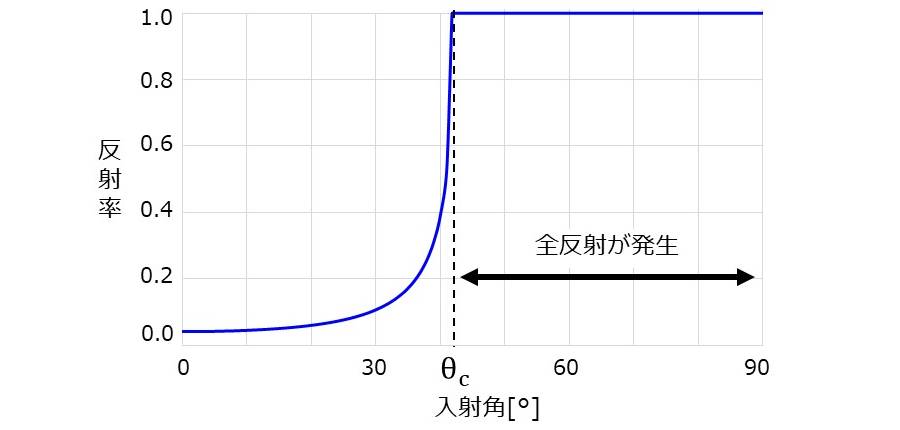
図2にフレネルの公式から計算された、ガラス(屈折率\(\hspace{2pt}\large{n=1.5}\hspace{2pt}\))から空気(屈折率\(\hspace{2pt}\large{n=1}\hspace{2pt}\))の境界にs偏光の光が入射したときの反射率を示しています。
図の横軸は、入射角の大きさであり、臨界角より大きい入射角で全反射が発生します。

【1-2】エバネッセント波の概要

エバネッセント波とは、全反射が発生するときに、物質の境界面で反射方向の反対側に電磁場が染み出る現象のことをいいます。図3にエバネッセント波が発生しているときの様子を図示します。

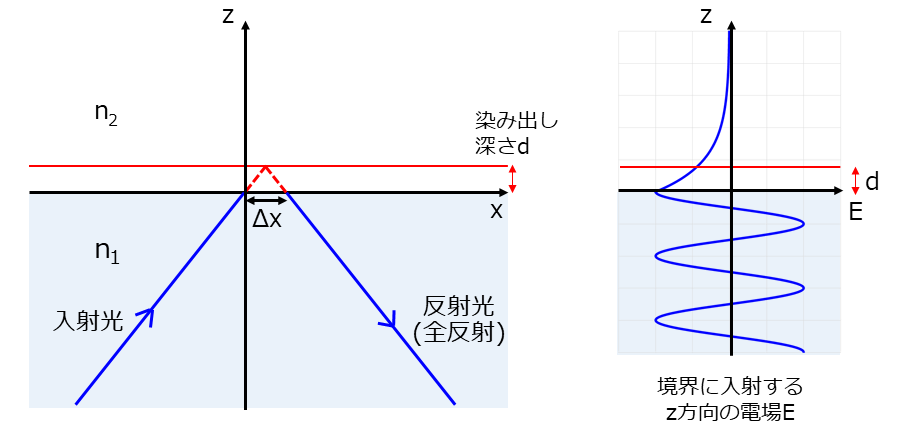
図3左は、xz平面における全反射が発生しているときの光の経路を図示しています。また、図3右は、縦軸に位置z、横軸に境界に入射する光の電場のz方向の成分を描いています。

光が境界面に入射すると、エバネッセント波が発生し、図3のz方向(境界面に垂直方向)に電場が染み出します。

このz方向に染み出た電場は、図3右のように、指数関数で減衰するのみであり、光のエネルギーは透過側に伝搬しないという特徴があります。

光の電場が透過側に染み出す距離を、染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)(penetration depth)といいます。染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)を計算する式については後述しています。

入射光は、あたかも染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)の位置で反射したかのように伝搬し、反射光のx方向の位置が図中の\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)だけずれることになります。

この反射光のx方向のズレ量\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)をグース・ヘンヒェンシフトといいます。

【2】エバネッセント波の染み出し深さの導出

本章では、エバネッセント波の染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)を求める式の導出をします。

【2-1】透過波の波数ベクトル

まず、エバネッセント波の式の導出のため、透過波の電場の波数ベクトル\(\hspace{2pt}\large{\boldsymbol{k_2}}\hspace{2pt}\)を求めます。

物質の境界面に法線からの角度\(\hspace{2pt}\large{\theta_1}\hspace{2pt}\)で入射した光が、角度\(\hspace{2pt}\large{\theta_2}\hspace{2pt}\)で透過するとします。
このとき、xz平面を伝搬する透過光の波数ベクトルを\(\hspace{2pt}\large{\boldsymbol{k_2}}\hspace{2pt}\)とします。

真空中の波数ベクトルの大きさを\(\hspace{2pt}\large{k_0}\hspace{2pt}\)とすると、屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の物質中の波数ベクトルの大きさ\(\hspace{2pt}\large{|\boldsymbol{k_2}|}\hspace{2pt}\)は\(\hspace{2pt}\large{n_2 k_0}\hspace{2pt}\)と表せます。 $$\large{|\boldsymbol{k_2}| = n_2 \hspace{1pt}k_0}$$ 下図のように、屈折角が\(\hspace{2pt}\large{\theta_2}\hspace{2pt}\)であるとき、透過光の波数ベクトルのx軸成分は\(\hspace{2pt}\large{n_2 \hspace{1pt}k_0 \hspace{1pt}\sin \theta_2}\hspace{2pt}\)、z軸成分は\(\hspace{2pt}\large{n_2 \hspace{1pt}k_0 \hspace{1pt}\cos \theta_2}\hspace{2pt}\)と表すことができます。

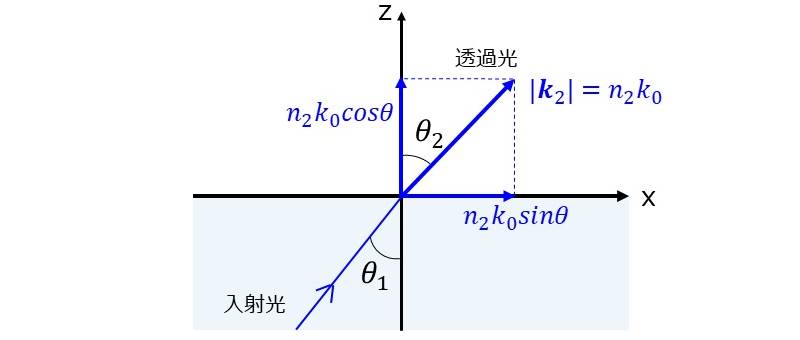
したがって、透過波の波数ベクトルは、\(\hspace{2pt}\large{(x,y,z)}\hspace{2pt}\)成分で表示すると以下のように表せます。 $$\large{\boldsymbol{k_2} = (n_2 \hspace{1pt}k_0 \hspace{1pt}\sin \theta_2 , 0 , n_2\hspace{1pt} k_0 \hspace{1pt}\cos \theta_2)}$$

上記の波数ベクトル\(\hspace{2pt}\large{\boldsymbol{k_2}}\hspace{2pt}\)を使用して、透過波の電場\(\hspace{2pt}\large{\boldsymbol{E_2}}\hspace{2pt}\)は以下のように表されます。 $$\large{\boldsymbol{E_2} = \boldsymbol{A_2} \exp [i(\boldsymbol{k_2} \cdot \boldsymbol{r} - \omega t )]\hspace{20pt}(1)}$$

【2-2】エバネッセント波の式の導出

屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)と屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の物質の境界面に光が入射したとき、スネルの法則から屈折角\(\hspace{2pt}\large{\theta_2}\hspace{2pt}\)は以下のように求められます。 $$\large{\sin \theta_2 = \frac{n_1}{n_2} \sin \theta_1\hspace{20pt}(2)}$$

全反射が発生するとき(入射角\(\hspace{2pt}\large{\theta_1}\hspace{2pt}\)が臨界角\(\hspace{2pt}\large{\theta_c}\hspace{2pt}\)より大きいとき)、\(\hspace{2pt}\large{\sin \theta_2 > 1}\hspace{2pt}\)が成立します。
ここで、(2)式を\(\hspace{2pt}\large{\cos \theta_2}\hspace{2pt}\)について整理すると以下のようになります。 $$\large{ \displaystyle \cos \theta_2 =\pm \sqrt{{1-\left(\frac{n_1}{n_2} \sin \theta_1 \right)}^2}}$$ \(\displaystyle\hspace{2pt}\large{ \frac{n_1}{n_2} \sin \theta_1 > 1}\hspace{2pt}\)であることから、虚数\(\hspace{2pt}\large{i}\hspace{2pt}\)を使用することで以下のように表します。 $$\large{ \displaystyle \cos \theta_2 =\pm i \hspace{2pt}\sqrt{{\left(\frac{n_1}{n_2} \sin \theta_1 \right)}^2 -1}\hspace{20pt}(3)}$$

全反射が発生するときの入射角と屈折角の条件である(3)式を、透過波の電場を表す(1)式に代入すると、以下の式を得ます。

ここで、(4)式中の\(\hspace{2pt}\large{\beta}\hspace{2pt}\)は以下の式で表されます。 $$\large{\beta = k_0 \sqrt{{{n_1}^2 \sin \theta_1 }^2-{n_2}^2}\hspace{20pt}} $$

(4)式の\(\hspace{2pt}\large{\exp [i\hspace{1pt}(n_2\hspace{1pt} k_0\hspace{1pt} \sin \theta_2 x - \omega \hspace{1pt}t )] }\hspace{2pt}\)は、\(\hspace{2pt}\large{x}\hspace{2pt}\)方向に進行する波を表しています。つまり、全反射が発生しているときも\(\hspace{2pt}\large{x}\hspace{2pt}\)軸方向に波が進行していることを意味します。

また、上式の\(\hspace{2pt}\large{\exp(+\beta z)}\hspace{2pt}\)の項は距離\(\hspace{2pt}\large{z}\hspace{2pt}\)に対して発散してしまい、現実の波を表現してないため、使用しません。

一方、\(\hspace{2pt}\large{ \exp(-\beta z)}\hspace{2pt}\)の項は、透過光の電場が距離\(\hspace{2pt}\large{z}\hspace{2pt}\)方向に指数関数で減少する様子を表します。この項がエバネッセント波を表現します。

【2-3】エバネッセント波の染み出し深さ

エバネッセント波による電場が、どれだけ透過側に染み出すかを、染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)といいます。
染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)は、境界面における電場の振れ幅が\(\displaystyle\hspace{2pt}\large{\frac{1}{e}}\hspace{2pt}\)になる距離\(\hspace{2pt}\large{z}\hspace{2pt}\)によって定義されます。

透過側の電場\(\hspace{2pt}\large{\boldsymbol{E_2}}\hspace{2pt}\)を、\(\hspace{2pt}\large{z}\hspace{2pt}\)方向の成分のみで表すと、以下のようになります。 $$\large{E_{2z} = A_{2z} \exp \left( - \beta z \right)}$$

上式より、電場\(\hspace{2pt}\large{E_{2z}}\hspace{2pt}\)の振れ幅が\(\displaystyle\hspace{2pt}\large{\frac{1}{e}}\hspace{2pt}\)となるとき、染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)を計算すると、以下のようになります。

\(\displaystyle\hspace{2pt}\large{k_0 = \frac{2 \pi}{\lambda}}\hspace{2pt}\)であることから、光の波長\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)を使用した染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)は以下のように表せます。

$$\large{d = \frac{\lambda}{2 \pi \sqrt{{{n_1}^2 \sin \theta_1 }^2-{n_2}^2}}}$$

【3】エバネッセント波の計算例

屈折率\(\hspace{2pt}\large{n_1=1.5}\hspace{2pt}\)のガラスから、屈折率\(\hspace{2pt}\large{n_2=1}\hspace{2pt}\)の空気の境界面に光が入射した場合について考えます。

境界面の法線に対して、入射光は角度\(\hspace{2pt}\large{45°}\hspace{2pt}\)で入射し、全反射が発生しているとします。また、入射する光の波長は 530nm の緑色の単色光であるとします。

このとき、ガラス中を伝搬する光の電場\(\hspace{2pt}\large{E_1}\hspace{2pt}\)が、境界面\(\hspace{2pt}\large{z=0}\hspace{2pt}\)に入射し、エバネッセント波として透過側の媒質(空気)に染み出す様子を示します。

図5は、縦軸にz軸方向に進行する電場の大きさ、横軸に位置\(\hspace{2pt}\large{z}\hspace{2pt}\)をnm単位で図示しています。(境界面\(\hspace{2pt}\large{z=0}\hspace{2pt}\)で電場の振れ幅が\(\hspace{2pt}\large{E_0}\hspace{2pt}\)として規格化しています。)

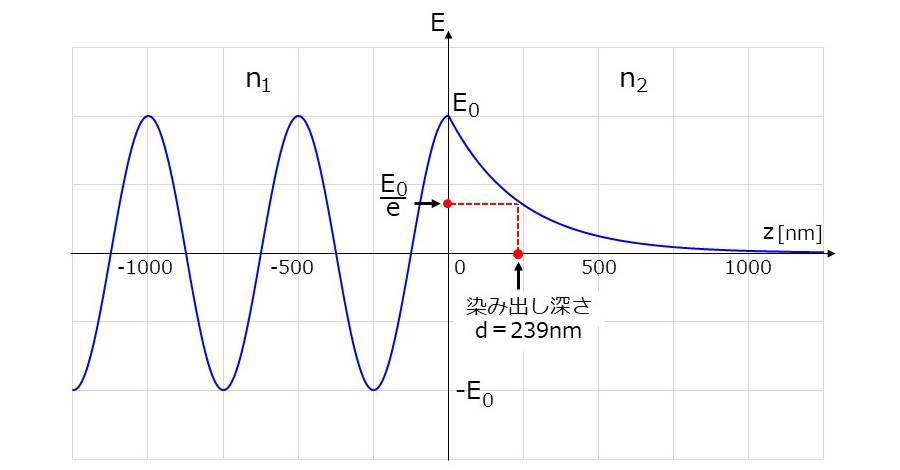
染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)の定義は、境界面における電場の振れ幅が\(\displaystyle\hspace{2pt}\large{\frac{1}{e}}\hspace{2pt}\)となる位置であるため、振れ幅が\(\displaystyle\hspace{2pt}\large{\frac{E_0}{e}}\hspace{2pt}\)となる位置が染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)となります。

屈折率\(\hspace{2pt}\large{n_1=1.5}\hspace{2pt}\)のガラスと屈折率\(\hspace{2pt}\large{n_2=1}\hspace{2pt}\)の空気の境界においては、染み出し深さ\(\hspace{2pt}\large{d}\hspace{2pt}\)は約239nmの位置になります。

また参考として、図5と同じ条件で、z方向に進行する電場が時間とともに境界に到達する様子を示します。

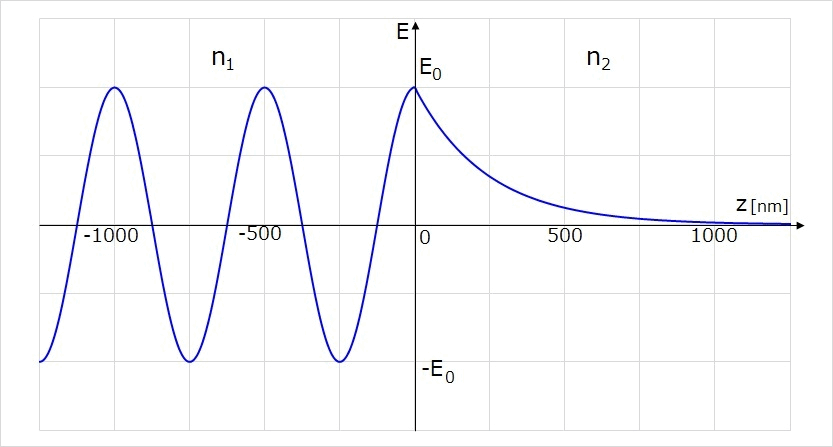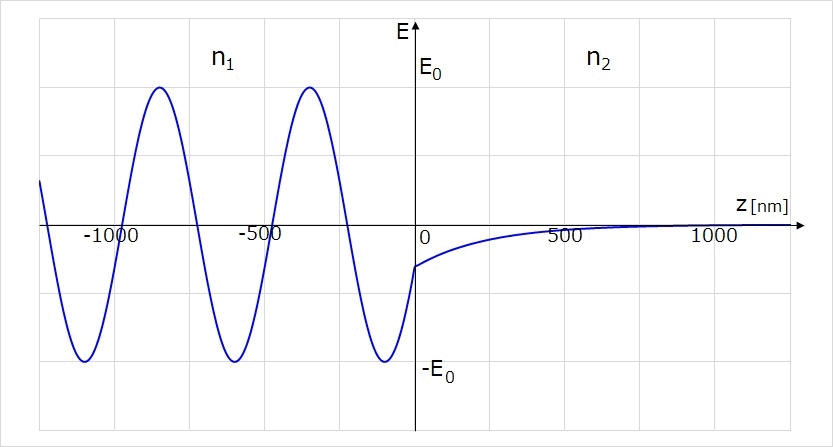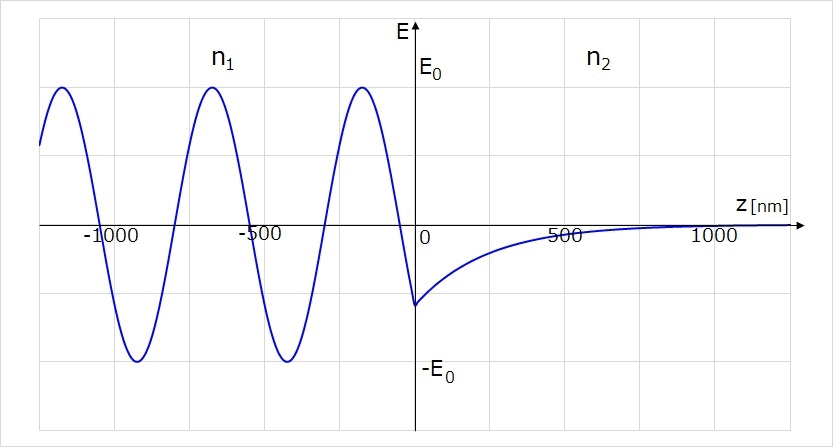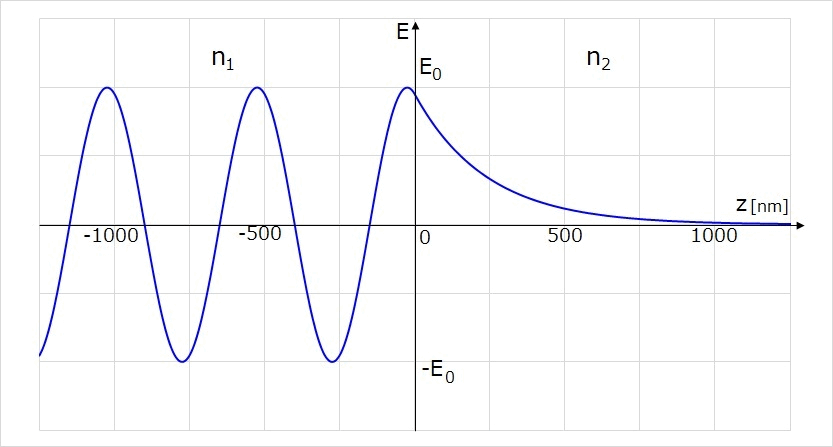
境界面に到達した光の電場が、\(\hspace{2pt}\large{z=0}\hspace{2pt}\)から指数関数で減衰して透過側に染み出している様子が分かります。

---