反射率と透過率の計算ツール
本ツールは以下の計算結果を出力します。
- (1)ブリュースター角の計算結果
- (2)境界面の反射率と透過率のグラフ
- (3)境界面の反射率と透過率の計算結果
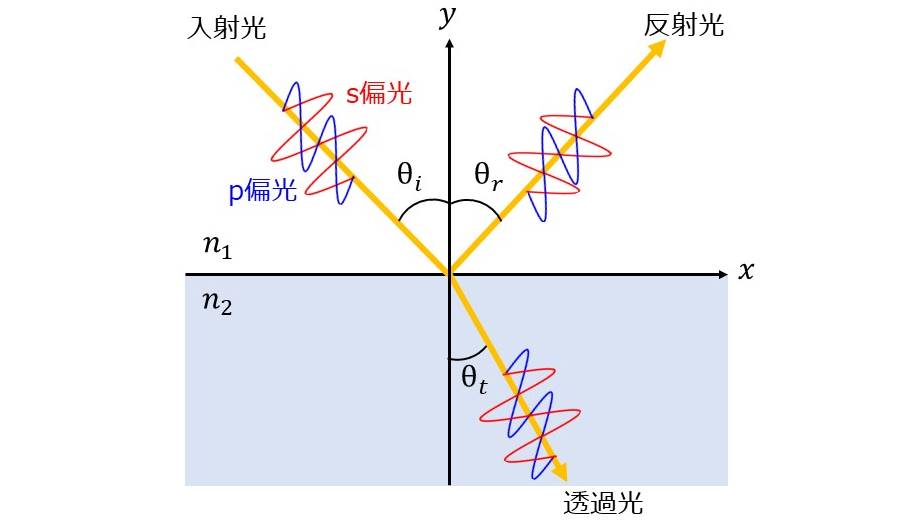
入射側と屈折側の屈折率から、ブリュースター角とフレネルの公式による反射率と透過率を計算します。
空欄に入射側と屈折側の媒質の絶対屈折率、入射角の刻み幅を入力し、『ブリュースター角の計算実行』と『反射率と透過率の計算実行』を押してください。
(※当サイトの提供する計算結果や情報については一切責任は負いません。)
入射側屈折率 n1
屈折側屈折率 n2
入射光の偏光
入射角の刻み幅
出力値の小数点以下の桁数
| ブリュースター角\(\large{\theta_B}\) |
|---|
| 入射角\(\large{\theta_1}\) | 反射率\(\large{R}\) | 透過率\(\large{T}\) |
|---|
(※ブリュースター角はp偏光の成分のみに発生します。)
計算ツールの説明
計算ツール内の計算方法や使い方の補足について記述しています。
ブリュースター角と反射率,透過率の計算式
p偏光の反射率がゼロとなるブリュースター角は以下の式により計算します。 $$\large{\theta_B=\tan^{-1} \left(\frac{n_2}{n_1}\right)}$$
s偏光の反射率\(\large{R_s}\),p偏光の反射率\(\large{R_p}\)は以下のフレネルの公式より計算します。 $$\large{R_s =(r_s)^2=\left(\frac{n_1\cos\theta_i-n_2\cos\theta_t}{n_1\cos\theta_i+n_2\cos\theta_t}\right)^2}$$ $$\large{R_p=(r_p)^2=\left(\frac{n_2\cos\theta_i-n_1\cos\theta_t}{n_2\cos\theta_i+n_1\cos\theta_t}\right)^2}$$
また、s偏光の透過率\(\large{T_s}\),p偏光の透過率\(\large{T_p}\)は、反射率と透過率の和が1であるとして計算しています。 $$\large{T_s = 1 -R_s}$$ $$\large{T_p = 1 -R_p}$$
無偏光は、p偏光成分とs偏光成分のエネルギーが50%ずつ存在している状態と考えられるため、反射率\(\large{R}\)、透過率\(\large{T}\)は以下の式で計算しています。 $$\large{R =\frac{R_s + R_p}{2}}$$ $$\large{T =\frac{T_s + T_p}{2}}$$
屈折率の参考
| 物質名 | 屈折率 |
|---|---|
| 空気(0℃,1atm) | 1.000193 |
| 水(20℃) | 1.333 |
| メチルアルコール | 1.329 |
| 石英ガラス | 1.459 |
| ダイアモンド | 2.417 |
計算ツールの説明
・『度数法』と『弧度法』のラジオボタンによって入射角の単位が設定されます。
(例)入射角を10°刻みで出力したい場合、『度数法[°]』に設定し、刻み幅に『10』と入力します。
・全反射が発生している時、反射率は1と表示されます。
・『出力値の小数点以下の桁数』では、入力された桁より1つ小さい桁で出力値を四捨五入します。
(例)『出力値の小数点以下の桁数』が2 → 出力が『10.59284...』の場合は、小数点以下3桁で四捨五入して『10.59』となります。
参考文献
表1のd線(589.3nm)における屈折率は、以下の文献(1),(2)を参考とした。
・(1)国立天文台『理科年表 平成27年』丸善出版株式会社,平成26年11月30日発行, pp463 光学的性質 光学ガラスの屈折率
・(2)山口重雄『屈折率』共立出版株式会社,昭和56年10月1日発行, pp16 表1-2 いろいろな物質の屈折率(波長=589nm)