ランベルト・ベールの法則
本項では、ランベルト・ベールの法則について解説します。
【1】ランベルト・ベールの法則
ランベルト・ベールの法則(Lambert-Beer's law)とは、試料中を光が伝搬するときの、吸収による光強度の減少量を表現する法則です。
溶液中を伝搬する光強度\(\hspace{2pt}\large{I}\hspace{2pt}\)は、溶液中の分子の吸収により、伝搬距離と溶液の濃度に比例した割合で減少します。
溶液中の物質のモル吸光係数を\(\hspace{2pt}\large{\epsilon^{*}\hspace{2pt}\mathrm{[cm^2 mol^{-1}]}}\hspace{2pt}\)、溶液の濃度を\(\hspace{2pt}\large{C\hspace{2pt}\mathrm{[mol\hspace{2pt}L^{-1}]}}\hspace{2pt}\)としたとき、 単位長さ(\(\hspace{2pt}\large{dL}\hspace{2pt}\))あたりの光強度\(\hspace{2pt}\large{dI}\hspace{2pt}\)は、モル吸光係数\(\hspace{2pt}\large{\epsilon^{*}}\hspace{2pt}\)と、溶液の濃度\(\hspace{2pt}\large{C}\hspace{2pt}\)に比例して減衰します。 $$\large{\displaystyle dI= -\epsilon^{*} C \times I dL\hspace{20pt}(1)}$$
試料に入射する光強度を\(\hspace{2pt}\large{I_0}\hspace{2pt}\)、試料中を\(\hspace{2pt}\large{L}\hspace{2pt}\)だけ伝搬したときの光強度を\(\hspace{2pt}\large{I(L)}\hspace{2pt}\)として、(1)式を解くことで、以下のランベルト・ベールの法則を導きます。
ランベルト・ベールの法則は、試料に入射する光強度\(\hspace{2pt}\large{I_0}\hspace{2pt}\)と、試料から透過した光強度\(\hspace{2pt}\large{I(L)}\hspace{2pt}\)の関係を示します。
例えば、長さLのガラスセルに溶液を入れ、光強度\(\hspace{2pt}\large{I_0}\hspace{2pt}\)で光を入射すると、(2)式にしたがって指数関数で光強度が減少し、光強度\(\hspace{2pt}\large{I(L)}\hspace{2pt}\)となり透過します。
【1-1】吸光度Aと透過度T
試料に入射する光強度\(\hspace{2pt}\large{I_0}\hspace{2pt}\)と、試料から透過した光強度\(\hspace{2pt}\large{I(L)}\hspace{2pt}\)の比を取った数値を、透過度Tといいます。
$$\large{T = \frac{I(L)}{I_0}}$$ここで、試料の透過度Tを常用対数で表した数値を、吸光度\(\hspace{2pt}\large{A}\hspace{2pt}\)といいます。 $$\large{A=-log_{10} \hspace{2pt} T=-log_{10}{\frac{I(L)}{I_0}}\hspace{20pt}}$$
ランベルト・ベールの法則を変形し、吸光度\(\hspace{2pt}\large{A}\hspace{2pt}\)をモル吸光係数\(\hspace{2pt}\large{\epsilon}\hspace{2pt}\)と、溶液の濃度Cで表現すると、以下のようになります。
実際の実験では、透過度Tから吸光度\(\hspace{2pt}\large{A}\hspace{2pt}\)やモル吸光係数\(\hspace{2pt}\large{\epsilon}\hspace{2pt}\)を求めるため、(2)式より(3)式の形でよく使用されます。
(2)式の形式のランベルト・ベールの法則は、自然対数の底eにより表記されることが一般的です。
一方、(3)式の吸光度\(\hspace{2pt}\large{A}\hspace{2pt}\)は、入射光と透過光の関係を常用対数で表記します。 このため、(3)式の導出には以下のように自然対数の底eから常用対数の底10に変換を行います。
\begin{eqnarray} \displaystyle \large I(L)&\large =&\large I_0 \hspace{2pt} e^{-\epsilon^{*}\hspace{2pt} C L} \\[0.7em] \displaystyle &\large =&\large I_0 \hspace{2pt} 10^{-\epsilon^{*}\hspace{2pt} C L \hspace{1pt} log_{10}\hspace{2pt}e}\\[0.7em] &\large =& \large I_0 \hspace{2pt} 10^{-\epsilon \hspace{2pt}C L} \end{eqnarray}このとき、\(\hspace{2pt}\large{\epsilon^{*}}\hspace{2pt}\)と\(\hspace{2pt}\large{\epsilon}\hspace{2pt}\)の関係は以下のようになります。 $$\large{\epsilon = \epsilon^{*} \hspace{2pt} log_{10}\hspace{2pt}e=0.434 \hspace{2pt} \epsilon^{*}}$$
【1-2】吸収スペクトル
吸光度\(\hspace{2pt}\large{A}\hspace{2pt}\)の大きさは測定する波長に依存して変化します。
縦軸を吸光度\(\hspace{2pt}\large{A}\hspace{2pt}\)、横軸を測定波長[nm] (もしくは、波数 [\(\hspace{2pt}\large{\mathrm{cm^{-1}}}\hspace{2pt}\)]) により表したグラフを吸収スペクトルもしくは、吸収曲線といいます。
図1に、吸収スペクトルの例を示します。
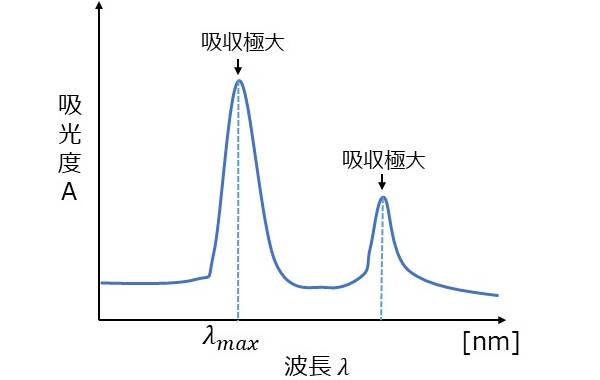
吸収スペクトルのピークとなっている箇所それぞれを吸収極大といいます。また、その波長を吸収極大波長といいます。
図1のように複数のピークが存在する場合、最も吸収の強いピークをその物質の吸収極大として、その波長を\(\hspace{2pt}\large{\lambda_{max}}\hspace{2pt}\)と書くことがあります。
吸収スペクトルは、原子や分子の構造や電子配置により物質固有の特性を示します。 実験により得られた吸収スペクトルの特徴から、定性分析が行われます。
参考文献
・(1)尾崎幸洋『分光法シリーズ 第2巻 近赤外分光法』講談社, 2015年3月23日 発行
・(2)飯田隆・澁川雅美・菅原正雄・鈴鹿敢・宮入伸一『イラストで見る化学実験の基礎知識』第2版,丸善株式会社,平成16年3月25年 発行