フレネルの公式の導出

本項では、以下の内容について解説します。

• ・フレネルの公式の導出方法
• ・フレネルの公式の変換(入射角、屈折角による表記)

【1】フレネルの公式の導出

フレネルの公式(Frenel equations)とは、異なる媒質の境界面において光が反射、屈折するときの、電場と磁場の振れ幅の関係を表す式です。

フレネルの公式により、反射や透過によって発生する位相変化や、反射率や透過率の計算を行うことができます。

本項では、フレネルの公式を導出する方法について解説しています。
(フレネルの公式による反射率と透過率については別項で解説しています。)

【1-1】フレネルの公式の概要

図1のように、屈折率の異なる媒質の境界面に光が入射したとき、反射光と透過光が生じます。

入射側の媒質の屈折率を\(\hspace{2pt}\large{n_1}\hspace{2pt}\)、透過側の媒質の屈折率を\(\hspace{2pt}\large{n_2}\hspace{2pt}\)とします。
また、入射角を\(\hspace{2pt}\large{\theta_i}\hspace{2pt}\)、反射角を\(\hspace{2pt}\large{\theta_r}\hspace{2pt}\)、屈折角を\(\hspace{2pt}\large{\theta_t}\hspace{2pt}\)とします。

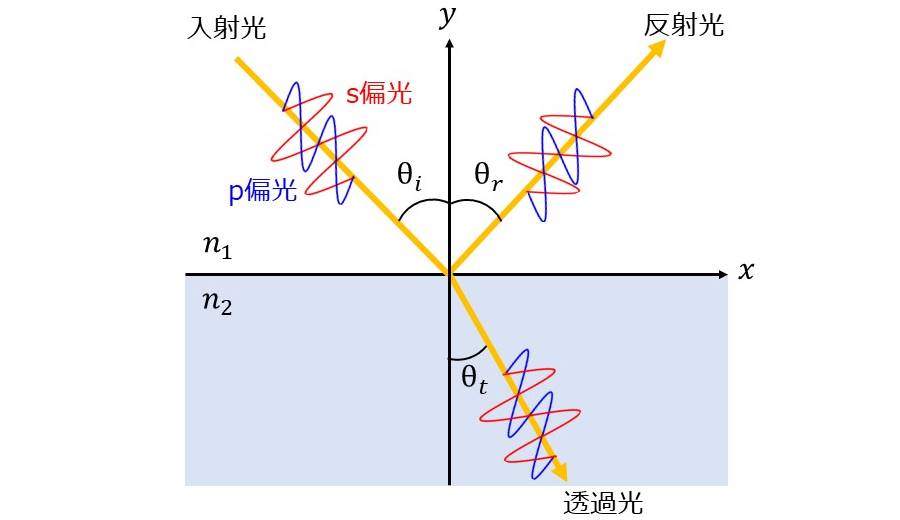
フレネルの公式では、入射光に対する反射光の振れ幅の比率を振幅反射係数\(\hspace{2pt}\large{r}\hspace{2pt}\)として表します。
一方、入射光に対する透過光の振れ幅の比率を振幅透過係数\(\hspace{2pt}\large{t}\hspace{2pt}\)として表します。

また、振幅反射係数\(\hspace{2pt}\large{r}\hspace{2pt}\)と振幅透過係数\(\hspace{2pt}\large{t}\hspace{2pt}\)は、s偏光とp偏光では異なる式によって計算されます。

s偏光の場合は、振幅反射係数を\(\hspace{2pt}\large{r_s}\hspace{2pt}\)、振幅透過係数を\(\hspace{2pt}\large{t_s}\hspace{2pt}\)と偏光状態を表す下付き文字を付けた記号を使用します。
(s偏光とp偏光については別項で解説しています。)

フレネルの公式は、以下の4つの式によって記述されます。

【1-2】フレネルの公式の導出方法

フレネルの公式は異なる媒質の境界面において、電場と磁場の境界面に平行な成分が連続であるという条件から導出されます。
このような境界面における電磁場の満たす条件を境界条件といいます。

先述したように、入射光が境界面に対して斜めに入射している場合、電場と磁場の振動方向によって、s偏光とp偏光という状態に分けられます。

本章では、s偏光とp偏光それぞれの場合のフレネルの公式の導出方法について解説します。

・s偏光のフレネルの公式の導出

s偏光では、図2のように電場はxy平面に垂直(境界面に対して平行)に振動します。一方、磁場はxy平面に対して平行(境界面に垂直)に振動します。

(図中の 丸の中に黒点がある記号 は図の前後方向、つまりxy平面に垂直な方向を意味します。)

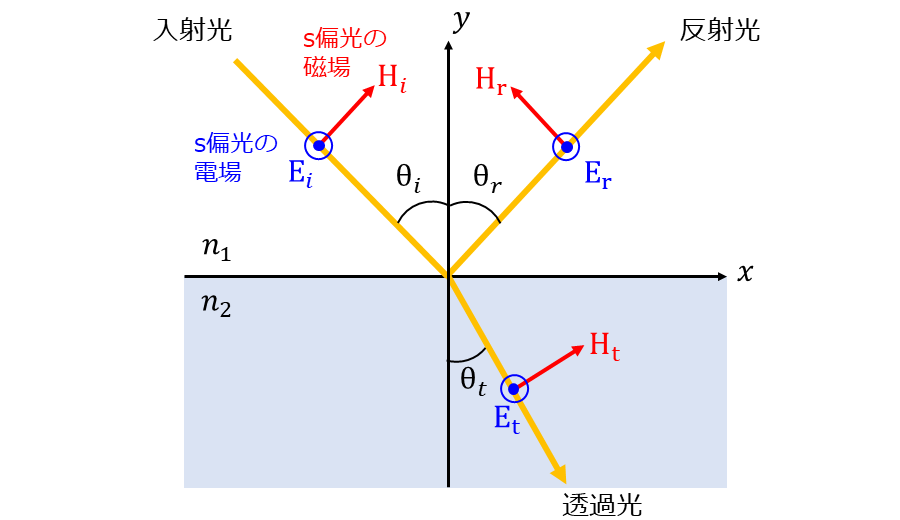
入射光、反射光、透過光の電場の振れ幅をそれぞれ\(\hspace{2pt}\large{E_i}\hspace{2pt}\)、\(\hspace{2pt}\large{E_r}\hspace{2pt}\)、\(\hspace{2pt}\large{E_t}\hspace{2pt}\)とすると、s偏光の電場は常に境界面に平行であるため、以下の式が成り立ちます。

$$\large{E_i + E_r = E_t\hspace{20pt}(5)}$$

一方、磁場に関してはx軸方向の成分が連続であると考えます。
以下の図のように、磁場の振れ幅のx成分とy成分に分解して計算を行います。

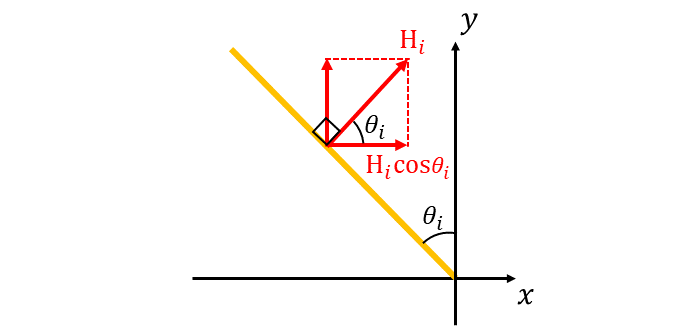
入射光、反射光、透過光の磁場の振れ幅をそれぞれ\(\hspace{2pt}\large{H_i}\hspace{2pt}\)、\(\hspace{2pt}\large{H_r}\hspace{2pt}\)、\(\hspace{2pt}\large{H_t}\hspace{2pt}\)とすると、以下の式が成り立ちます。 $$\large{H_i \cos \theta_i - H_r \cos \theta_r = H_t \cos \theta_t}$$

ここで、マクスウェル方程式から誘電率\(\hspace{2pt}\large{\epsilon}\hspace{2pt}\)、透磁率\(\hspace{2pt}\large{\mu}\hspace{2pt}\)の媒質中の、電場と磁場の振れ幅には以下の関係が成り立ちます。 $$\large{E=\sqrt{\frac{\mu}{\epsilon}}H}$$

電場と磁場の振れ幅の関係を使用して磁場の式を書き換えると、以下のようになります。

振幅反射係数\(\hspace{2pt}\large{r_s}\hspace{2pt}\)は、入射する電場の振れ幅と反射する電場の振れ幅の比により計算されます。

したがって、(5)式と(6)式から振幅反射係数\(\displaystyle\hspace{2pt}\large{r_s=\frac{E_r}{E_i}}\hspace{2pt}\)を求めると、以下のようになります。(\(\hspace{2pt}\large{\theta_i = \theta_r}\hspace{2pt}\)を使用しています。) $$\large{ \displaystyle {r_s = \frac{E_r}{E_i} = \frac{\sqrt{\frac{\epsilon_1}{\mu_1}} \cos \theta_i - \sqrt{\frac{\epsilon_2}{\mu_2}} \cos \theta_t}{\sqrt{\frac{\epsilon_1}{\mu_1}} \cos \theta_i+ \sqrt{\frac{\epsilon_2}{\mu_2}} \cos \theta_t }}}$$

また、振幅透過係数\(\hspace{2pt}\large{t_s}\hspace{2pt}\)は、入射する電場の振れ幅と透過する電場の振れ幅の比により計算されます。

したがって、(5)式と(6)式から振幅透過係数\(\displaystyle\hspace{2pt}\large{t_s=\frac{E_t}{E_i}}\hspace{2pt}\)は、以下のようになります。 $$\large{ \displaystyle {t_s =\frac{E_t}{E_i} = \frac{2\sqrt{\frac{\epsilon_1}{\mu_1}} \cos \theta_i}{\sqrt{\frac{\epsilon_1}{\mu_1}} \cos \theta_i+ \sqrt{\frac{\epsilon_2}{\mu_2}} \cos \theta_t }}}$$

一般的な誘電体の透磁率は、真空中の透磁率\(\hspace{2pt}\large{\mu_0}\hspace{2pt}\)とほぼ一致すると考えられます。
したがって、\(\hspace{2pt}\large{\mu_1 \approx \mu_2 \approx \mu_0}\hspace{2pt}\)とすることができます。

また、屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)と誘電率\(\hspace{2pt}\large{\epsilon}\hspace{2pt}\)、透磁率\(\hspace{2pt}\large{\mu}\hspace{2pt}\)は、\(\displaystyle\large{n = \frac{\sqrt{\epsilon \mu}}{\sqrt{\epsilon_0 \mu_0}}}\hspace{2pt}\)の関係があることから、上式の\(\hspace{2pt}\large{\epsilon, \mu}\hspace{2pt}\)を削除することで、以下の式に書き換えられます。

・p偏光のフレネルの公式の導出

p偏光では、図4のように磁場は境界面に対して平行に振動します。
一方、電場は境界面に垂直な面(xy平面)を振動します。

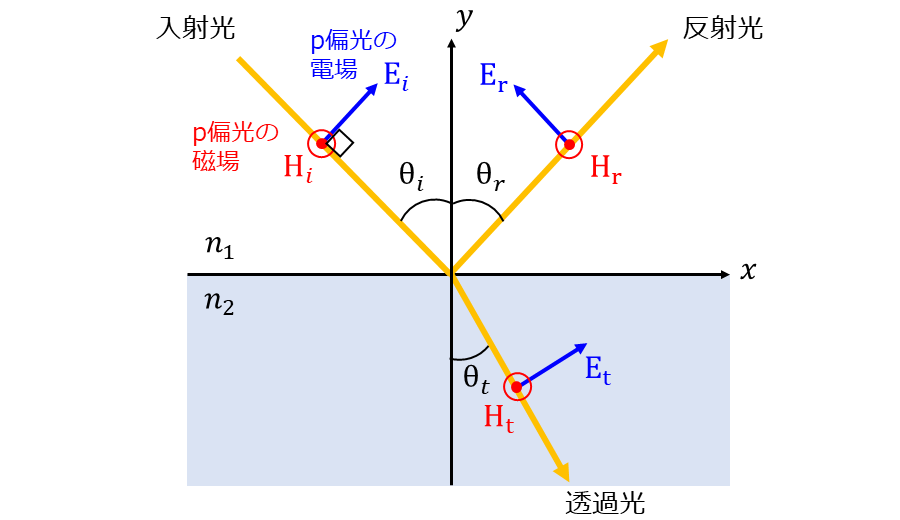
p偏光では磁場が常に境界に面に平行であるため、以下の式が成り立ちます。

$$\large{H_i + H_r = H_t}$$

また、電場はx軸方向の成分が連続であるとして以下が成り立ちます。 $$\large{E_i \cos \theta_i - E_r \cos \theta_r = E_t \cos \theta_t}$$

s偏光と同様な計算により、p偏光の振幅反射係数\(\hspace{2pt}\large{r_p}\hspace{2pt}\)を計算すると以下のようになります。 $$\large{ \displaystyle {r_p = \frac{E_r}{E_i} = \frac{\sqrt{\frac{\epsilon_2}{\mu_2}} \cos \theta_i - \sqrt{\frac{\epsilon_1}{\mu_1}} \cos \theta_t}{\sqrt{\frac{\epsilon_2}{\mu_2}} \cos \theta_i + \sqrt{\frac{\epsilon_1}{\mu_1}} \cos \theta_t }}}$$

また、振幅透過係数\(\hspace{2pt}\large{t_p}\hspace{2pt}\)は以下のようになります。 $$\large{ \displaystyle {t_p = \frac{E_t}{E_i} = \frac{2\sqrt{\frac{\epsilon_1}{\mu_1}} \cos \theta_i }{\sqrt{\frac{\epsilon_2}{\mu_2}} \cos \theta_i + \sqrt{\frac{\epsilon_1}{\mu_1}} \cos \theta_t }}}$$

また、振幅反射係数\(\hspace{2pt}\large{r_p}\hspace{2pt}\)と振幅透過係数\(\hspace{2pt}\large{t_p}\hspace{2pt}\)を屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)を用いて表すと以下のようになります。

【1-3】フレネルの公式のまとめ

これまで導いたs偏光、p偏光の振幅反射係数と振幅透過係数をフレネルの公式といいます。

フレネルの公式を改めてまとめると以下のようになります。

フレネルの公式は、スネルの法則\(\hspace{2pt}\large{(n_1\sin\theta_i=n_2\sin\theta_t)}\hspace{2pt}\)と連立させることで、入射角\(\hspace{2pt}\large{\theta_i}\hspace{2pt}\)と屈折角\(\hspace{2pt}\large{\theta_t}\hspace{2pt}\)の式(1)'～(4)'に変換することができます。 (詳しい変換の方法については、次の章で解説しています。)

【2】フレネルの公式の変換

媒質の屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)、\(\hspace{2pt}\large{n_2}\hspace{2pt}\)を使用した振幅反射係数、振幅透過係数の式(1)～(4)を、入射角\(\hspace{2pt}\large{\theta_i}\hspace{2pt}\)と屈折角\(\hspace{2pt}\large{\theta_t}\hspace{2pt}\)のみの式(1)'～(4)'に変換する方法を解説します。

・s偏光の振幅反射係数

s偏光の振幅反射係数\(\hspace{2pt}\large{r_s}\hspace{2pt}\)は以下の式により記述されます。 $$\large{r_s=\frac{n_1\cos\theta_i-n_2\cos\theta_t}{n_1\cos\theta_i+n_2\cos\theta_t}}$$

ここで、スネルの法則から屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)と屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の媒質間で以下の式が成り立ちます。 $$\large{\frac{n_2}{n_1} = \frac{\sin \theta_i}{\sin \theta_t}}$$

スネルの法則を使用し、振幅反射係数\(\hspace{2pt}\large{r_s}\hspace{2pt}\)の式から屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)、\(\hspace{2pt}\large{n_2}\hspace{2pt}\)を削除すると以下の式となります。 $$\large{r_s = \frac{\sin \theta_t \cos \theta_i - \sin \theta_i \cos \theta_t}{\sin \theta_t \cos \theta_i + \sin \theta_i \cos \theta_t}}$$

ここで、三角関数の加法定理(\(\hspace{2pt}\large{\sin{(\alpha \pm \beta)}=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta}\hspace{2pt}\))から以下の関係が成り立ちます。 $$\large{r_s=-\frac{\sin(\theta_i-\theta_t)}{\sin(\theta_i+\theta_t)}}$$

・s偏光の振幅透過係数

s偏光の振幅透過係数\(\hspace{2pt}\large{t_s}\hspace{2pt}\)は以下の式により記述されます。 $$\large{t_s=\frac{2n_1\cos\theta_i}{n_1\cos\theta_i+n_2\cos\theta_t}}$$

スネルの法則を使用し、振幅透過係数\(\hspace{2pt}\large{t_s}\hspace{2pt}\)の式から屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)、\(\hspace{2pt}\large{n_2}\hspace{2pt}\)を削除すると以下の式となります。 $$\large{t_s = \frac{2 \sin \theta_t \cos \theta_i}{\sin \theta_t \cos \theta_i + \sin \theta_i \cos \theta_t}}$$

ここで、三角関数の加法定理(\(\hspace{2pt}\large{\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta}\hspace{2pt}\))から、以下の式に書き換えられます。 $$\large{t_s = \frac{2 \sin \theta_t \cos \theta_i}{\sin (\theta_i + \theta_t)}}$$

・p偏光の振幅反射係数

p偏光の振幅反射係数\(\hspace{2pt}\large{r_p}\hspace{2pt}\)は以下の式により記述されます。 $$\large{r_p=\frac{n_2\cos\theta_i-n_1\cos\theta_t}{n_2\cos\theta_i+n_1\cos\theta_t}}$$

スネルの法則を使用し、振幅反射係数の式から屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)、\(\hspace{2pt}\large{n_2}\hspace{2pt}\)を削除すると以下の式となります。 $$\large{r_p = \frac{\sin \theta_i \cos \theta_i - \sin \theta_t \cos \theta_t}{\sin \theta_i \cos \theta_i + \sin \theta_t \cos \theta_t}}$$

ここで、三角関数の2倍角の公式(\(\hspace{2pt}\large{\sin {2 \alpha} = 2 \sin \alpha \cos \alpha}\hspace{2pt}\))から、以下の式に書き換えられます。 $$\large{r_p = \frac{\sin {2 \theta_i}-\sin {2 \theta_t}}{\sin {2 \theta_i}+\sin {2 \theta_t}}}$$

さらに、三角関数の和積の公式(\(\hspace{2pt}\large{\sin \alpha \pm \sin \beta = 2 \sin \frac{\alpha \pm \beta}{2} \cos \frac{\alpha \mp \beta}{2}}\hspace{2pt}\))から、以下の式に変形できます。 $$\large{r_p = \frac{\cos{(\theta_i + \theta_t)} \sin{(\theta_i - \theta_t)}}{\sin{(\theta_i + \theta_t)}\cos{(\theta_i - \theta_t)}}}$$ したがって、以下の式が成り立ちます。 $$\large{r_p = \frac{\tan{(\theta_i - \theta_t)}}{\tan{(\theta_i + \theta_t)}}}$$

・p偏光の振幅透過係数

p偏光の振幅透過係数\(\hspace{2pt}\large{t_p}\hspace{2pt}\)は以下の式により記述されます。 $$\large{t_p=\frac{2n_1\cos\theta_i}{n_2\cos\theta_i+n_1\cos\theta_t}}$$

スネルの法則を使用し、振幅反射係数の式から屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)、\(\hspace{2pt}\large{n_2}\hspace{2pt}\)を削除すると以下の式となります。 $$\large{t_p=\frac{2 \sin \theta_t \cos\theta_i}{\sin \theta_i \cos\theta_i+\sin \theta_t \cos\theta_t}}$$

ここで、三角関数の2倍角の公式(\(\hspace{2pt}\large{\sin {2 \alpha} = 2 \sin \alpha \cos \alpha}\hspace{2pt}\))から、以下の式に書き換えられます。 $$\large{t_p=\frac{2 \sin \theta_t \cos\theta_i}{\frac{1}{2}\sin2 \theta_i +\frac{1}{2} \sin 2 \theta_t }}$$

さらに、三角関数の和積の公式(\(\hspace{2pt}\large{\sin \alpha + \sin \beta = 2 \sin \frac{\alpha + \beta}{2} \cos \frac{\alpha - \beta}{2}}\hspace{2pt}\))から、以下の式に変形できます。 $$\large{t_p=\frac{2 \cos\theta_i \sin \theta_t }{\sin{(\theta_i + \theta_t)}\cos{(\theta_i - \theta_t)} }}$$

参考文献

---