ドルーデモデル
本項では以下の内容を解説しています。
- ・ドルーデモデルとは
- ・誘電関数(比誘電率)の導出
- ・屈折率や消衰係数、反射率との関係
【1】ドルーデモデルとは
ドルーデモデルとは、物質中の自由電子に対し古典的な運動方程式を用いて、光の電場と自由電子の相互作用(誘電関数)を記述するモデルです。
ドルーデモデルにより誘電関数を計算することにより、金属の屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)や消衰係数\(\hspace{2pt}\large{\kappa}\hspace{2pt}\)、反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)などを計算することができます。
【1-1】ローレンツモデルの運動方程式
ドルーデモデルと対比されるモデルとして、ローレンツモデルがあります。ローレンツモデルとは、電子が原子に束縛されているとしたモデルです。
ローレンツモデルによる電子の運動方程式は、以下の式で表されます。
上式では、時刻\(\hspace{2pt}\large{t}\hspace{2pt}\)における電子の位置を\(\hspace{2pt}\large{x(t)}\hspace{2pt}\)、電子の質量を\(\hspace{2pt}\large{m_0}\hspace{2pt}\)、固有振動数を\(\hspace{2pt}\large{\omega_0}\hspace{2pt}\)としています。
また、\(\hspace{2pt}\large{-e}\hspace{2pt}\)は電子の電荷、\(\hspace{2pt}\large{E(t)}\hspace{2pt}\)は光の電場を表します。したがって、(1)式の右辺は光の電場により電子に加わる外力を表しています。
(1)式の左辺の第1項は電子の加速を表す項です。また、第2項は電子の速度に比例したエネルギーの損失を表す項です。(\(\hspace{2pt}\large{\gamma}\hspace{2pt}\)は緩和定数といいます。)
また、(1)式の左辺の第3項は、電子の位置に比例して発生する復元力を表しています。
ローレンツモデルでは、この項によって電子が原子に束縛されていることを表しています。
【1-2】ドルーデモデルの運動方程式
一方、ドルーデモデルでは自由電子に対して運動方程式を立てます。
自由電子とは原子から束縛を受けずに運動する電子のことであり、(1)式で復元力が働かない場合に相当します。
つまり、(1)式で固有振動数を\(\hspace{2pt}\large{\omega_0=0}\hspace{2pt}\)とすることで、ドルーデモデルによる運動方程式となります。
$$\large{\displaystyle m_0 \frac{d^2 x}{d t^2} +m_0 \frac{1}{\tau} \frac{dx}{dt} = -e E_x (t)\hspace{15pt}(2)}$$
ドルーデモデルとローレンツモデルを比較すると、電子の位置に比例して発生する復元力\(\hspace{2pt}\large{m_0\hspace{1pt} {\omega_0}^2}\hspace{1pt}x(t)\hspace{2pt}\)が存在しない点が異なります。
また、ドルーデモデルでは、第2項の緩和定数\(\hspace{2pt}\large{\gamma}\hspace{2pt}\)の代わりに、緩和時間\(\hspace{2pt}\large{\tau}\hspace{2pt}\)の逆数を使用しています。(すなわち、\(\displaystyle\hspace{2pt}\large{\gamma = \frac{1}{\tau}}\hspace{2pt}\)としています。)
ドルーデモデルでは、電場によって加速された電子が他の原子に衝突し減速すると考え、電子の衝突する確率を\(\displaystyle\hspace{2pt}\large{\frac{1}{\tau}}\hspace{2pt}\)により表します。
【1-3】ドルーデモデルによる誘電関数の導出
ローレンツモデルと同様な手順でドルーデモデルによる比誘電率(誘電関数)を求めることができます。
(2)式の右辺は、光の電場によって電荷\(\hspace{2pt}\large{-e}\hspace{2pt}\)の電子が受ける外力を表しています。光の電場が\(\hspace{2pt}\large{x}\hspace{2pt}\)方向に振幅\(\hspace{2pt} \large{\tilde{E}_0}\hspace{2pt}\)、周波数\(\hspace{2pt}\large{\omega}\hspace{2pt}\)で振動しているとして以下の式により書き表します。 $$\large{ E_x(t)= \tilde{E}_0 e^{-i \omega t}}$$
また、電子の位置\(\hspace{2pt}\large{x(t)}\hspace{2pt}\)は、光の電場と同じ周波数\(\hspace{2pt}\large{\omega}\hspace{2pt}\)で振動しているとして、以下の式で表します。 $$\large{x(t) = \tilde{x}_0 e^{-i \omega t}}$$
(2)式に光の電場\(\hspace{2pt}\large{E_x(t)}\hspace{2pt}\)と電子の位置\(\hspace{2pt}\large{x(t)}\hspace{2pt}\)を代入し、光の電場の振幅\(\hspace{2pt}\large{\tilde{E}_0}\hspace{2pt}\)と電子の振幅\(\hspace{2pt} \large{\tilde{x}_0}\hspace{2pt}\)の関係を得ます。 $$\large{\tilde{x}_0 = \frac{e}{m_0( \omega^2 + i \hspace{1pt}\omega\hspace{1pt} \tau^{-1})}\tilde{E}_0\hspace{15pt}(3)}$$
ここで、自由電子の分極\(\hspace{2pt}\large{P}\hspace{2pt}\)は、単位体積あたりの電子の個数\(\hspace{2pt}\large{N}\hspace{2pt}\)を用いて以下の式で計算されます。 $$\large{P = -N \hspace{1pt} e \hspace{1pt} \tilde{x}_0}$$
上式に(3)式を代入すると、以下のように分極\(\hspace{2pt}\large{P}\hspace{2pt}\)が求められます。
\begin{eqnarray} \large P&=&\large -N \hspace{1pt} e \hspace{1pt} \tilde{x}_0\\[0.7em] \large &=&\large -\frac{N e^2}{m_0}\frac{1}{ \omega^2 + i \hspace{1pt}\omega \hspace{1pt}\tau^{-1}}\tilde{E}_0\\ \end{eqnarray}ここで、物質中のマクスウェル方程式から、物質中の電束密度\(\hspace{2pt}\large{\boldsymbol{D}}\hspace{2pt}\)は、電場\(\hspace{2pt}\large{\boldsymbol{E}}\hspace{2pt}\)と分極\(\hspace{2pt}\large{\boldsymbol{P}}\hspace{2pt}\)に対して以下の関係があります。 $$\large{\boldsymbol{D} = \epsilon_0 \boldsymbol{E} + \boldsymbol{P} = \epsilon_0 \hspace{1pt}\tilde{\epsilon_r}\hspace{1pt} \boldsymbol{E}\hspace{20pt}(4)}$$
上式の\(\hspace{2pt}\large{ \epsilon_0}\hspace{2pt}\)は真空中の誘電率、\(\hspace{2pt}\large{ \tilde{\epsilon_r}}\hspace{2pt}\)は物質中の比誘電率です。 比誘電率\(\hspace{2pt}\large{ \tilde{\epsilon_r}}\hspace{2pt}\)は誘電関数ともいわれます。
(3)式から、ドルーデモデルによる比誘電率(誘電関数)を求めることができます。
ここで、\(\displaystyle\large{\frac{N e^2}{\epsilon_0 m_0} = \omega_p^2}\hspace{2pt}\)と置き換えます。\(\hspace{2pt}\large{\omega_p}\hspace{2pt}\)はプラズマ振動数といい、電子の振動が、光の電場の振動に追従できなくなる限界の周波数を意味しています。
また、自由電子以外の電子からの寄与を背景誘電率\(\hspace{2pt}\large{\epsilon_b}\hspace{2pt}\)とすると、ドルーデモデルによる比誘電率(誘電関数)は以下のように書き表されます。 $$\large{ \displaystyle \tilde{\epsilon_r}(\omega) = \epsilon_b-\frac{{\omega_p}^2}{ \omega^2 + i \omega \tau^{-1}}}$$
ここで、比誘電率\(\hspace{2pt}\large{\tilde{\epsilon_r}}\hspace{2pt}\)の実部を\(\hspace{2pt}\large{\epsilon_1(\omega)}\hspace{2pt}\)、虚部を\(\hspace{2pt}\large{\epsilon_2(\omega)}\hspace{2pt}\)とすると、以下のようになります。 $$\large{ \epsilon_1(\omega) = \epsilon_b - \frac{{\omega_p}^2}{ \omega^2 + \tau^{-2}}}$$ $$\large{ \epsilon_2(\omega) = \frac{{\omega_p}^2 \tau^{-1} }{\omega(\omega^2+\tau^{-2})}}$$
【2】屈折率,消衰係数,反射率の計算
ドルーデモデルから求められる比誘電率(誘電関数)と、屈折率や消衰係数、反射率の関係について解説します。
【2-1】誘電関数と屈折率,消衰係数の関係
前章で求めた比誘電率の実部\(\hspace{2pt}\large{\epsilon_1(\omega)}\hspace{2pt}\)と虚部\(\hspace{2pt}\large{\epsilon_2(\omega)}\hspace{2pt}\)を縦軸、周波数\(\hspace{2pt}\large{\omega}\hspace{2pt}\)を横軸にとったグラフの概形を示します。
まず、図1に減衰項が存在しない(\(\displaystyle\hspace{2pt}\large{\frac{1}{\tau}=0}\hspace{2pt}\))としてグラフを描いています。
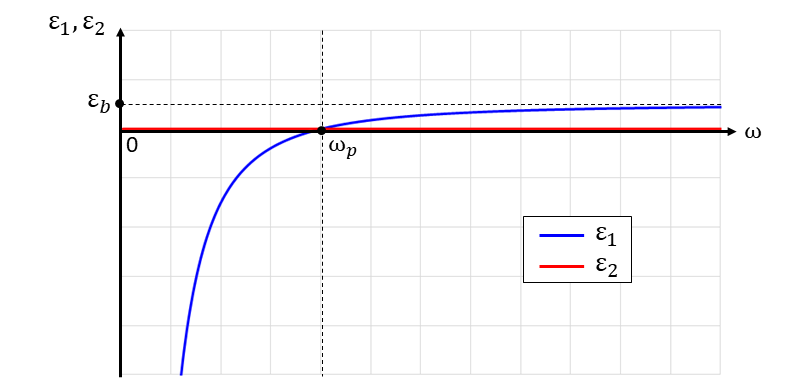
図1より、プラズマ振動数\(\hspace{2pt}\large{\omega_p}\hspace{2pt}\)より小さい範囲では、実部\(\hspace{2pt}\large{\epsilon_1}\hspace{2pt}\)が負となり、比誘電率は負の実数となります。
ここで、比誘電率の実部\(\hspace{2pt}\large{\epsilon_1}\hspace{2pt}\)、虚部\(\hspace{2pt}\large{\epsilon_2}\hspace{2pt}\)と屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)、消衰係数\(\hspace{2pt}\large{\kappa}\hspace{2pt}\)は以下のような関係式があります。
(比誘電率と屈折率、消衰係数の関係式については屈折率|複素屈折率で解説しています。)
上式から屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)と消衰係数\(\hspace{2pt}\large{\kappa}\hspace{2pt}\)の周波数依存性の概形を描いたグラフが以下のようになります。
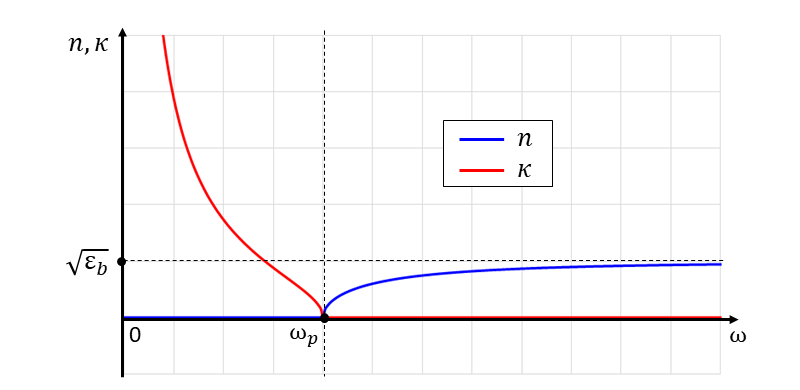
【2-2】反射率の計算
ここで、上記の図2の屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)、消衰係数\(\hspace{2pt}\large{\kappa}\hspace{2pt}\)から反射率を計算します。
空気(屈折率\(\hspace{2pt}\large{n=1}\hspace{2pt}\))から複素屈折率\(\hspace{2pt}\large{\tilde{n}}\hspace{2pt}\)の物質に垂直に光が入射したときの反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)は以下のように求められます。
$$\large{R=\left|\frac{\tilde{n}-1}{\tilde{n}+1}\right|^2=\frac{(n-1)^2+\kappa^2}{(n+1)^2+\kappa^2}}$$
上式から反射スペクトルを計算すると、図3のようなグラフが得られます。
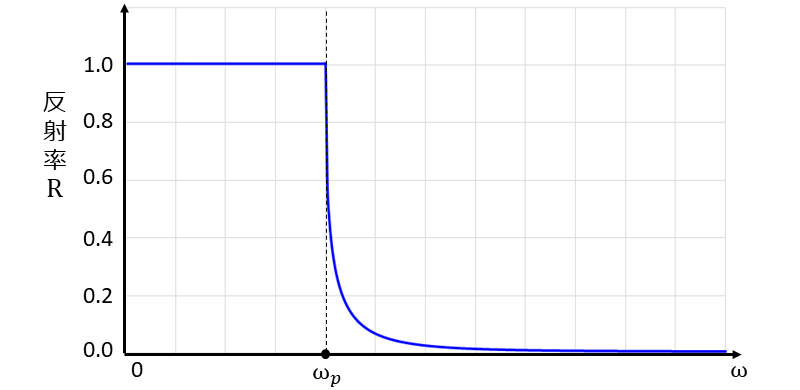
図3より、プラズマ振動数\(\hspace{2pt}\large{\omega_p}\hspace{2pt}\)より小さい周波数では、反射率が1となっていることが分かります。
これはプラズマ振動数より周波数が小さい領域\(\hspace{2pt}\large{\omega < \omega_p}\hspace{2pt}\)では、自由電子が変位することで光の電場を打ち消し、内部に光が伝搬できないために生じます。
一方、プラズマ振動数より周波数が大きい領域\(\hspace{2pt}\large{\omega > \omega_p}\hspace{2pt}\)では、光の吸収に関連する消衰係数\(\hspace{2pt}\large{\kappa}\hspace{2pt}\)が0となり、光が吸収されず透過し、反射率が低下します。
どのような計算によってプラズマ振動数\(\hspace{2pt}\large{\omega_p}\hspace{2pt}\)より小さい周波数で、反射率が1となるのかを整理します。
先述したようにプラズマ振動数より周波数\(\hspace{2pt}\large{\omega}\hspace{2pt}\)が小さい領域では、比誘電率\(\hspace{2pt}\large{\epsilon_r}\hspace{2pt}\)は負の実数となります。
このとき、ある正の実数を\(\hspace{2pt}\large{a}\hspace{2pt}\)とすると、比誘電率\(\hspace{2pt}\large{\epsilon_r}\hspace{2pt}\)は以下に記述できます。 $$\large{\epsilon_r = \epsilon_1 + i \epsilon_2=-a}$$ したがって、屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)は以下のように計算されます。 $$\large{n = \frac{1}{\sqrt{2}} \sqrt{-a + \sqrt{{(-a)}^2 + {0}^2}}=0}$$ また、消衰係数\(\hspace{2pt}\large{\kappa}\hspace{2pt}\)は以下のように計算されます。 $$\large{\kappa=\frac{1}{\sqrt{2}} \sqrt{ a + \sqrt{{(-a)}^2 + {0}^2}}=\sqrt{a}}$$
よって、反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)は以下のように求められます。 $$\large{R=\frac{(n-1)^2+\kappa^2}{(n+1)^2+\kappa^2}=\frac{1+a}{1+a}=1}$$
したがって、比誘電率\(\hspace{2pt}\large{\epsilon_r}\hspace{2pt}\)が負の実数となるときに反射率が1となることが分かります。
実際の自由電子の運動には、エネルギーの損失が存在するため、(\(\displaystyle\hspace{2pt}\large{\frac{1}{\tau} \neq 0}\hspace{2pt}\))となります。
減衰項が存在する条件(\(\displaystyle\hspace{2pt}\large{\frac{1}{\tau}=0.03}\hspace{2pt}\))における比誘電率の実部\(\hspace{2pt}\large{\epsilon_1}\hspace{2pt}\)、虚部\(\hspace{2pt}\large{\epsilon_2}\hspace{2pt}\)と、屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)、消衰係数\(\hspace{2pt}\large{\kappa}\hspace{2pt}\)と、反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)を並べたグラフを示します。
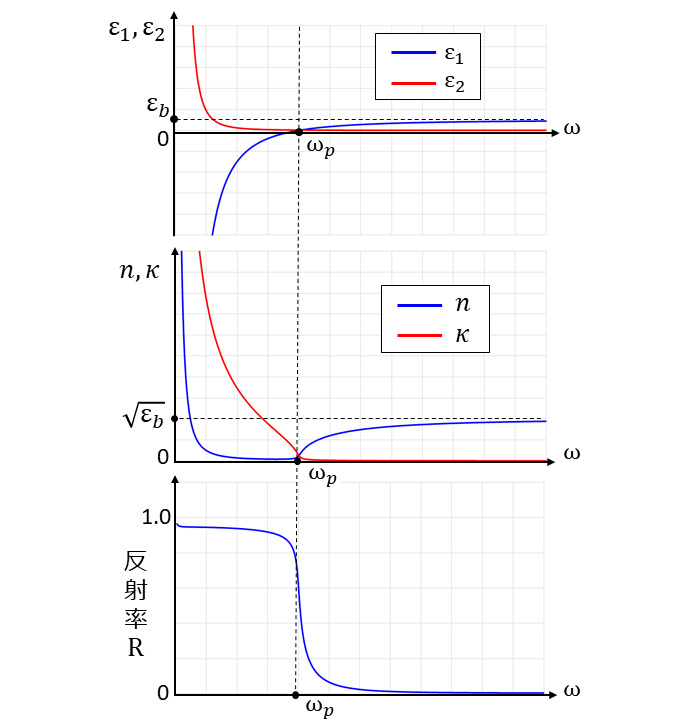
減衰項が存在する場合、図3と比較して反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)の変化が緩やかになりますが、プラズマ振動数\(\hspace{2pt}\large{\omega_p}\hspace{2pt}\)より小さい領域では高い反射率を持っていることが分かります。
金属に特有な光沢は、可視光線の波長の範囲に高い反射率を持つために生じています。
【3】参考文献
・(1)斎藤 博,今井 和明,大石 正和,澤田 孝幸,鈴木 和彦『入門 固体物性 -基礎からデバイスまで-』共立出版株式会社,2011年9月25日 初版15刷発行,pp150-161