スネルの法則の導出

本項では、ホイヘンスの原理やフェルマーの原理を使用したスネルの法則の導出について解説します。

スネルの法則の公式や問題については、別の記事で詳しく解説しています。
また、屈折角や臨界角を計算するツールを別のページで作成しています。

スネルの法則(snell's law)とは、異なる屈折率の媒質の境界に光が入射したときの入射角と屈折角の関係を表す式です。

図1のように、入射側の屈折率を\(\hspace{2pt}\large{n_1}\hspace{2pt}\)、透過側の屈折率を\(\hspace{2pt}\large{n_2}\hspace{2pt}\)とします。 また、境界面の法線を基準とした入射角を\(\hspace{2pt}\large{\theta_1}\hspace{2pt}\)、屈折角を\(\hspace{2pt}\large{\theta_2}\hspace{2pt}\)とします。

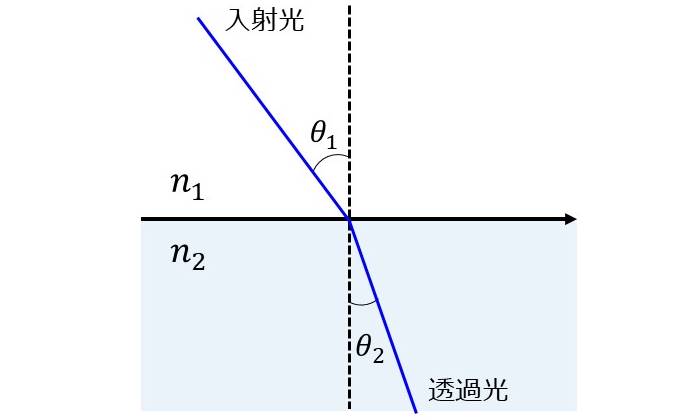
このとき、入射角\(\hspace{2pt}\large{\theta_1}\hspace{2pt}\)と屈折角\(\hspace{2pt}\large{\theta_2}\hspace{2pt}\)の間には、以下の関係式が成り立ちます。

本項では、上記のスネルの法則をホイヘンスの原理とフェルマーの原理から導出する方法について解説します。

【1】ホイヘンスの原理によるスネルの法則の導出

本章では、ホイヘンスの原理によってスネルの法則を導出します。

【1-1】ホイヘンスの原理の説明

ホイヘンスの原理は、空間に広がる波の位相の等しい面(波面)が、時間の経過に従ってどのように進行するかを説明をします。

ホイヘンスの原理によると、空間に波が伝わるとき、波面上の点が次の新しい波源となります。この新しい波源から生じた波を二次波といいます。

均質な媒質中の場合、波の伝わる速さが\(\hspace{2pt}\large{v}\hspace{2pt}\)のとき、2次波は時刻\(\hspace{2pt}\large{t}\hspace{2pt}\)後に半径\(\hspace{2pt}\large{v \hspace{1pt} t}\hspace{2pt}\)の球面として広がると描くことができます。二次波を重ね合わせた包絡線が次の波面となります。

【1-2】平面波の屈折の作図

ここで、図2のように、屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)、屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の媒質の境界に平面波の光が入射する場合を考えます。

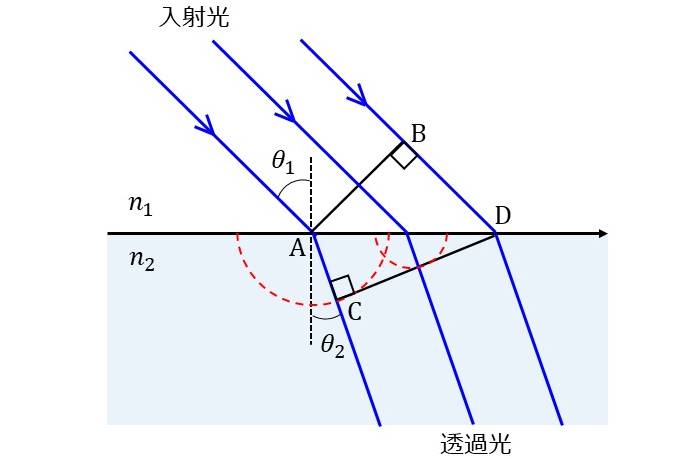
平面波は、境界面に入射角\(\hspace{2pt}\large{\theta_1}\hspace{2pt}\)で入射しているとします。図中のABは入射光の進行方向に対して垂直であり、位相の等しい面を表しています。

このとき、点Aの位置の光波は境界に到達しているため、屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の媒質中を進行します。

一方、点Bの位置の光波は境界に達するまでに屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)の媒質中をある時間だけ進行する必要があります。

境界ADを波源とした二次波を考えると、点Aの位置の二次波が最も半径が大きく、点Dに近づくにつれて半径が小さくなります。
この二次波の包絡線を描くと、図1のように点Dの位置から各二次波に接線を引いた形状となります。
この接線\(\hspace{2pt}\large{\overline{AD}}\hspace{2pt}\)が屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)中の媒質中の波面となります。

【1-3】ホイヘンスの原理によるスネルの法則の導出

図2のホイヘンスの原理による屈折の作図から、スネルの法則を導出します。

ある時刻に点Bの位置を通過した光波が、時間\(\hspace{2pt}\large{t}\hspace{2pt}\)だけかけて媒質の境界である点Dに到達したとします。

このとき、BD間の距離は、屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)中の光の速度\(\hspace{2pt}\large{v_1}\hspace{2pt}\)を使用し、以下のように表すことができます。(式中の\(\hspace{2pt}\large{c}\hspace{2pt}\)は真空中の光速です。) $$\large{\displaystyle \overline{BD} = v_1 t = \frac{c \hspace{1pt} t}{n_1}\hspace{20pt}(1)}$$

また、ある時刻に点Aの位置に到達した光波は、時間\(\hspace{2pt}\large{t}\hspace{2pt}\)の間に屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の媒質中を\(\displaystyle\hspace{2pt}\large{v_2\hspace{1pt} t = \frac{c\hspace{1pt}t}{n_2}}\hspace{2pt}\)だけ進行します。

ホイヘンスの原理から、点Aを波源とした二次波は半径\(\displaystyle\hspace{2pt}\large{v_2 \hspace{1pt}t = \frac{c\hspace{1pt}t}{n_2}}\hspace{2pt}\)の球面として描かれます。よって、距離\(\hspace{2pt}\large{\overline{AC}}\hspace{2pt}\)が二次波の半径の大きさであるとすると、以下のようになります。 $$\large{\displaystyle \overline{AC} = v_2\hspace{1pt} t = \frac{c\hspace{1pt}t}{n_2}\hspace{20pt}(2)}$$

ここで、図2より\(\hspace{2pt}\large{\angle BAD = \theta_1}\hspace{2pt}\)、\(\hspace{2pt}\large{\angle ADC = \theta_2}\hspace{2pt}\)となります。 したがって、以下の式が成り立つことが分かります。 $$\large{\displaystyle \frac{\overline{BD}}{\overline{AC}}= \frac{\overline{AD}\sin{\theta_1}}{\overline{AD}\sin{\theta_2}}=\frac{\sin{\theta_1}}{\sin{\theta_2}}\hspace{20pt}(3)}$$

(1)～(3)式より、スネルの法則が導出されます。 $$\large{\displaystyle \frac{n_2}{n_1} = \frac{v_1}{v_2} =\frac{\sin{\theta_1}}{\sin{\theta_2}}}$$

【2】フェルマーの原理によるスネルの法則の導出

フェルマーの原理からスネルの法則を導出します。

【2-1】フェルマーの原理の説明

フェルマーの原理とは、光の伝進する経路を説明する基本的な原理であり、 "ある1点から他の1点に進行する光は、その2点間の光路長を極小値となる経路を通る"と説明されます。

光路長が極小値となる経路は、"光が2点間を進行する時間が極小値となる経路"でもあるため、本章では媒質を進行する時間が極小になるという条件で、スネルの法則を導出します。

図3のように、点P(0,a)から出た光線が、媒質の境界点O(x,0)で屈折した後、点Q(b,c)に到達する光の経路について考えます。

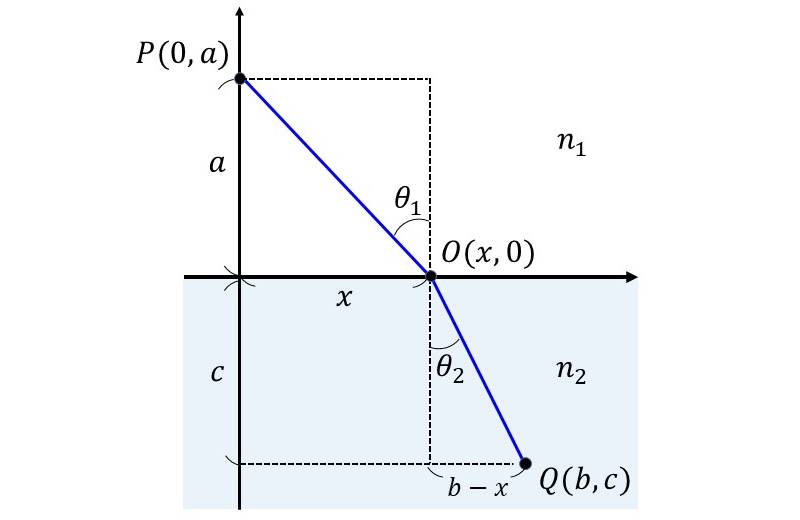
【2-2】フェルマーの原理からスネルの法則の導出

ここで、点Pは屈折率\(\hspace{2pt}\large{n_1}\hspace{2pt}\)の媒質中、点Qは屈折率\(\hspace{2pt}\large{n_2}\hspace{2pt}\)の媒質中に存在するとします。 点Oのx座標を変数として、点Pから点Qに到達する時間が極小値となる経路を求めることにより、スネルの法則を導出します。

点Pから出た光線が点Qに到達するまでの時間は、媒質1を進行する速さ\(\hspace{2pt}\large{v_1}\hspace{2pt}\)、媒質2を進行する速さ\(\hspace{2pt}\large{v_2}\hspace{2pt}\)を使用して以下のように求められます。 $$\large{t=\frac{\overline{PO}}{v_1}+\frac{\overline{OQ}}{v_2}\hspace{20pt}(4)}$$

(4)式をP点,O点,Q点のそれぞれの座標により書き表すと、以下のようになります。 $$\large{t=\frac{\sqrt{a^2+x^2}}{v_1}+\frac{\sqrt{{(b-x)}^2+c^2}}{v_2}\hspace{20pt}(5)}$$

点Pから点Qまで到達する時間\(\hspace{2pt}\large{t}\hspace{2pt}\)が、境界点の位置\(\hspace{2pt}\large{x}\hspace{2pt}\)に対して極小値となるとき、\(\displaystyle\hspace{2pt}\large{\frac{dt}{dx}=0}\hspace{2pt}\)を満たします。(5)式の時間\(\hspace{2pt}\large{t}\hspace{2pt}\)を微分すると、(6)式となります。

ここで、境界面に対する入射角を\(\hspace{2pt}\large{\theta_1}\hspace{2pt}\)、屈折角を\(\hspace{2pt}\large{\theta_2}\hspace{2pt}\)とすると、以下が成り立ちます。 \begin{eqnarray} \large \sin{\theta_1}&\large =&\large \frac{x}{\sqrt{a^2+x^2}}\\[0.7em] \large \sin{\theta_2}&\large =&\large \frac{b-x}{\sqrt{{(b-x)}^2+c^2}} \end{eqnarray}

上式を(6)式に代入することで、媒質中の光の速さと入射角、屈折角の関係を得ることができます。 $$\large{\frac{\sin{\theta_1}}{\sin{\theta_2}}=\frac{v_1}{v_2}}$$

ここで、\(\displaystyle\hspace{2pt}\large{v_1=\frac{c}{n_1}}\hspace{2pt}\)と\(\displaystyle\hspace{2pt}\large{v_2=\frac{c}{n_2}}\hspace{2pt}\)であることから、以下が成り立ちます。 $$\large{\frac{\sin{\theta_1}}{\sin{\theta_2}}=\frac{n_2}{n_1}=\frac{v_1}{v_2}}$$ 以上から、スネルの法則を導出することができます。

参考文献

---