-光と光学に関連する用語の解説サイト-

真空中のマクスウェル方程式

本項では、真空中のマクスウェル方程式から光の波動方程式を導出し、電磁波の一般解や真空中の光速などについて解説します。

1. 真空中のマクスウェル方程式
- 1-1. マクスウェル方程式から波動方程式の導出
- 1-2. 真空中の光速の導出
2. 波動方程式の解
- 2-1. 波動方程式の一般解
- 2-2. 波動方程式の正弦波の解
3. 計算問題(電場の磁場の振動方向と大きさの関係)
4. 参考文献

【1】真空中のマクスウェル方程式

真空中のマクスウェル方程式は、電荷や電流などが存在しない空間で時間変化する電場$\large{\boldsymbol{E}}$ と磁場$\large{\boldsymbol{B}}$ の関係を表す式です。

真空中のマクスウェル方程式により、電場$\large{\boldsymbol{E}}$ と磁場$\large{\boldsymbol{B}}$ は互いに垂直に振動しながら光速$\large{c}$ の速さで空間を伝搬するという性質が導かれます。

電場$\large{\boldsymbol{E}}$ と磁場$\large{\boldsymbol{B}}$ が互いに振動しながら伝搬する波を電磁波といいます。
光は電磁波の一種であり、干渉や回折といった光の波としての性質は、光が電磁波であることから説明されます。

真空中におけるマクスウェル方程式は、以下の $\large{4\hspace{1pt}}$式により与えられます。

【真空中のマクスウェル方程式】

\begin{eqnarray} \large &&\large\boldsymbol{\nabla} \times \boldsymbol{E} = - \frac{\partial \boldsymbol{B}}{\partial t}\hspace{21pt}(1) \\[0.5em] \large &&\large\boldsymbol{\nabla} \times \boldsymbol{B} = \epsilon_0 \mu_0 \frac{\partial \boldsymbol{E}}{\partial t}\hspace{12pt}(2) \\[0.7em] \large &&\large\boldsymbol{\nabla} \cdot \boldsymbol{E} = 0\hspace{48pt}(3) \\[0.9em] \large &&\large\boldsymbol{\nabla} \cdot \boldsymbol{B} = 0\hspace{48pt}(4) \\[0.7em] \end{eqnarray}

ここで、$\large{\epsilon_0}$ は真空中の誘電率, $\large{\mu_0}$ は真空中の透磁率を表します。

$\large{\boldsymbol{\nabla} \times \boldsymbol{E}}$ はベクトル場の回転を表しており、直交座標系において電場の成分を $\large{\boldsymbol{E}=(E_x\hspace{1pt},\hspace{1pt}E_y\hspace{1pt},\hspace{1pt}E_z)}$ とすると以下のようになります。

$$\large{\displaystyle \hspace{10pt}\boldsymbol{\nabla} \times \boldsymbol{E}=\left(\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z},\hspace{2pt}\frac{\partial E_x}{\partial z}-\frac{\partial E_z}{\partial x},\hspace{2pt}\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}\right)\hspace{10pt}}$$

また、$\large{\boldsymbol{\nabla} \cdot \boldsymbol{E}}$ はベクトル場の発散を表しており、直交座標系において電場の成分を $\large{\boldsymbol{E}=(E_x\hspace{1pt},\hspace{1pt}E_y\hspace{1pt},\hspace{1pt}E_z)}$ とすると以下のようになります。 $$\large{\boldsymbol{\nabla} \cdot \boldsymbol{E}} = \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y}+ \frac{\partial E_z}{\partial z}$$ $\large{\boldsymbol{\nabla} \cdot \boldsymbol{E}}$ は電場ベクトルの発散を表しています。真空中では電荷が存在しない、すなわち電場の発散がゼロであるため、 $$\large{\boldsymbol{\nabla} \cdot \boldsymbol{E}} = 0$$ となります。

【1-1】マクスウェル方程式から波動方程式の導出

上記のマクスウェル方程式から、真空中を伝搬する光(電磁波)の波動方程式を導出します。

(1)式の両辺に $\large{\rm{rot}}$ ($\large{\nabla \times}$) を作用させると、以下の式となります。 $$\large{\displaystyle \boldsymbol{\nabla} \times (\boldsymbol{\nabla} \times \boldsymbol{E}) = - \frac{\partial}{\partial t}(\boldsymbol{\nabla} \times \boldsymbol{B})}$$ 上式に(2)式を代入し、$\large{\boldsymbol{B}}$ を削除すると以下の式が成り立ちます。 $$\large{\displaystyle \boldsymbol{\nabla} \times (\boldsymbol{\nabla} \times \boldsymbol{E}) = -\epsilon_0 \mu_0 \frac{\partial^2 \boldsymbol{E}}{\partial t^2}}$$ ここで、ベクトルの恒等式として以下の式が成り立ちます。 $$\large{\boldsymbol{\nabla} \times (\boldsymbol{\nabla} \times \boldsymbol{E}) = \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \boldsymbol{E}) - \boldsymbol{\nabla^2} \boldsymbol{E}}$$ また、(3)式から $\large{\boldsymbol{\nabla} \cdot \boldsymbol{E} = 0}$ であることを利用すると、以下の式が求められます。 $$\large{\boldsymbol{\nabla^2} \boldsymbol{E} = \epsilon_0 \mu_0 \frac{\partial^2 \boldsymbol{E}}{\partial t^2}}$$ 上記の式の変形は磁場$\large{\boldsymbol{B}}$ に対しても成り立ちます。

以上から、マクスウェル方程式から電場$\large{\boldsymbol{E}}$ と磁場$\large{\boldsymbol{B}}$ の波動方程式が導出されます。

【真空中の電場と磁場の波動方程式】

$\large{\displaystyle \boldsymbol{\nabla^2} \boldsymbol{E} - \epsilon_0 \hspace{1pt}\mu_0 \frac{\partial^2 \boldsymbol{E}}{\partial t^2}=0}$

$\large{\displaystyle \boldsymbol{\nabla^2} \boldsymbol{B} - \epsilon_0\hspace{1pt} \mu_0 \frac{\partial^2 \boldsymbol{B}}{\partial t^2}=0}$

【1-2】真空中の光速の導出

波動方程式とは、水面の波や音波など振動する物理現象に一般的に現れる方程式です。
波の変位量を $\large{\boldsymbol{\psi}}$ とするとき、$\large{\displaystyle \boldsymbol{\nabla^2}\boldsymbol{\psi} - \frac{1}{{\color{red}{v}\color{black}{}\hspace{1pt}}^2}\frac{\partial^2 }{\partial t^2} \boldsymbol{\psi}=0}$ により記述される波の位相速度は、$\large{\color{red}{v}}$ となります。

したがって、真空中の電場と磁場の波動方程式と比較すると、光(電磁波)の位相速度、すなわち真空中の光速$\large{c}$ は以下のようになります。 $$\large{c = \frac{1}{\sqrt{\epsilon_0 \mu_0}}}$$

上式から、真空中の光速$\large{c}$ は真空中の誘電率$\large{\epsilon_0}$ と真空中の透磁率$\large{\mu_0}$ の積により計算され、波長に依存せず一定の値になることが分かります。

光速$\large{c}$ を利用して電場と磁場の波動方程式を書き直すと、以下の式となります。

【真空中の電場と磁場の波動方程式】

$\large{\displaystyle \boldsymbol{\nabla^2} \boldsymbol{E} - \frac{1}{c^2} \frac{\partial^2 \boldsymbol{E}}{\partial t^2}=0}\hspace{10pt}(5)$

$\large{\displaystyle \boldsymbol{\nabla^2} \boldsymbol{B} - \frac{1}{c^2} \frac{\partial^2 \boldsymbol{B}}{\partial t^2}=0}\hspace{10pt}(6)$

【2】波動方程式の解

真空中の電場と磁場の波動方程式から、空間を伝搬する光(電磁波)の式について解説します。

【2-1】波動方程式の一般解

本章では、簡単に $\large{z\hspace{2pt}}$軸方向に伝搬する光のみを考えます。このとき、上記の波動方程式$\large{(5)}$ を直交座標系で書き表すと以下のようになります。 $$\large{\displaystyle \frac{\partial^2 \boldsymbol{E}}{\partial z^2} - \frac{1}{{c}^2}\frac{\partial^2 \boldsymbol{E}}{\partial t^2} =0\hspace{20pt}(5)'}$$ この波動方程式$\large{(5)'}$ の一般解は以下のようになります。 $$\large{\boldsymbol{E}(z,t)= f_+(z-ct) + f_-(z+ct)}$$ ここで、$\large{f_+}$は $\large{z\hspace{2pt}}$軸の$\large{\hspace{1pt}+}$方向に進行する波の関数、$\large{f_-}$ は $\large{z\hspace{2pt}}$軸の$\large{\hspace{1pt}-}$方向に進行する波の関数を表します。

波動方程式の一般解は、具体的な関数の形ではなく、時間$\large{t}$ だけ経過すると距離$\large{c\hspace{1pt}t}$ だけ移動する関数$\large{f}$ を表しています。

例えば、よく使われる波の式として正弦波 $\large{f(z,t) = A \cos(z-c\hspace{1pt}t)}$ は上記の波動方程式$\large{(5)'}$ を満たします。
また、正規分布の形状を表す $\large{f(z,t) = \mathrm{e}^{-a(z-c\hspace{1pt}t)^2}}$ も波動関数の解となります。

$\large{f(z,t) = A \cos(z-c\hspace{1pt}t)}$ と $\large{f(z,t) = \mathrm{e}^{-a(z-c\hspace{1pt}t)^2}}$ は異なる関数の形をしていますが、変数に $\large{(z-c\hspace{1pt}t)}$ を持っているため、どちらも波動方程式の解となります。

【2-2】波動方程式の正弦波の解

先述したように、波動方程式の一般解は変数に $\large{(z-c\hspace{1pt}t)}$, $\large{(z+c\hspace{1pt}t)}$ を持つ関数であり、具体的な関数の形を与えません。
そこで、波動方程式$\large{(5)'}$ 式を満たす最も基本的な解として、正弦波の式がよく用いられます。

位相速度が光速$\large{\hspace{1pt}c\hspace{2pt}}$、波長が $\large{\lambda}$ の $\large{z\hspace{1pt}}$軸の正方向に進行する正弦波は、以下のように表されます。 $$\large{\boldsymbol{E}(z,t)= \boldsymbol{E_0} \cos \frac{2 \pi}{\lambda}(z-c t +\phi)}$$ $\large{\boldsymbol{E_0}}$ は振動する電場の振幅、$\large{\phi}$ は初期位相を表します。
(上式が波動方程式を満たすことは、$\large{(5)'}$ に代入することで確かめられます。)

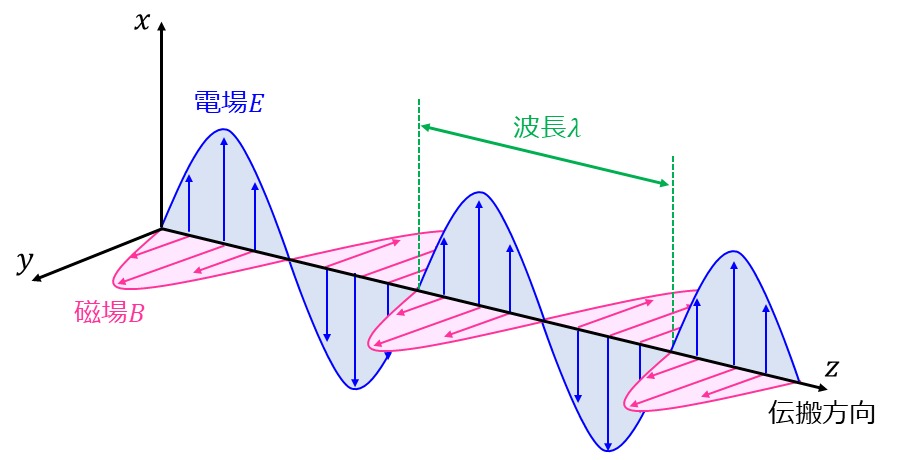
以下の図1に電場と磁場が正弦波として伝わるイメージを示します。光の電場と磁界の振動の様子を説明する図

図1.電場と磁場が正弦波で伝搬するイメージ

正弦波の波の式には様々な表現がありますが、よく使用される波数 $\displaystyle\large{k=\frac{2 \pi}{\lambda}}$、角周波数$\large{\omega=ck}$ により変形すると以下のようになります。(屈折率$\large{n}$ の物質中では $\displaystyle\large{\omega=\frac{ck}{n}}$ の関係があります。真空中では屈折率が $\large{n=1}$ であるため、$\large{\omega=ck}$ となります。) $$\large{\boldsymbol{E}(z,t)= \boldsymbol{E_0} \cos(kz-\omega t +\phi)}$$

また、$\large{z\hspace{1pt}}$軸のマイナス方向に進行している場合は、以下のように書き表せます。 $$\large{\boldsymbol{E}(z,t)= \boldsymbol{E_0} \cos(kz+\omega t+\phi)}$$

電場の波動方程式の解が $\large{\boldsymbol{E}(z,t)= \boldsymbol{E_0} \cos(kz-\omega t +\phi)}$ であるとき、磁場$\large{\boldsymbol{B}}$ は電場$\large{\boldsymbol{E}}$ と同じ位相$\large{(kz- \omega t+\phi)}$ で振動します。 $$\large{\boldsymbol{B}(z,t)= \boldsymbol{B_0} \cos(kz- \omega t+\phi)}$$

図1で描かれているように、光(電磁波)として伝わる電場$\large{\boldsymbol{E}}$ と磁場$\large{\boldsymbol{B}}$ は、互いに垂直に振動するという性質があります。次の章の計算問題では電場を正弦波の式で表し、電場$\large{\boldsymbol{E}}$ と磁場$\large{\boldsymbol{B}}$ は、互いに垂直に振動するという性質を導出します。

【3】マクスウェル方程式に関連した計算問題

本章では、マクスウェル方程式に関連した計算問題について解説します。

・電場と磁場の振動方向と大きさの関係

【問題】
$\large{z\hspace{2pt}}$軸の正方向に伝搬する光(電磁波)の電場$\large{\boldsymbol{E}}$ が $\large{x\hspace{2pt}}$軸方向のみに振動しているとする。
このときの磁場$\large{\boldsymbol{B}}$ の振動方向と、電場と磁場の振幅の大きさの関係を求めよ。

【回答と解説】
問題のような $\large{x\hspace{2pt}}$軸方向のみに振動している光は直線偏光の状態を指します。

電場$\large{\boldsymbol{E}}$ が $\large{x\hspace{2pt}}$軸方向のみの成分を持っているとして、マクスウェル方程式を解くことで磁場$\large{\boldsymbol{B}}$ の振動方向を導出します。

$\large{x\hspace{1pt}}$成分のみが正弦波で振動している電場$\large{\boldsymbol{E}}$ を以下の式で表します。 $$\large{\boldsymbol{E} =(E_x\hspace{1pt},\hspace{1pt}E_y\hspace{1pt},\hspace{1pt}E_z) = (E_{x0} \cos(kz-\omega t) , 0, 0)}$$

ここで、真空中のマクスウェル方程式の(1)式 $\displaystyle\large{\boldsymbol{\nabla} \times \boldsymbol{E} = - \frac{\partial \boldsymbol{B}}{\partial t}}$ を直交座標系で書くと以下のようになります。 $$\large{ \frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z} = -\frac{\partial B_x}{\partial t} }$$ $$\large{ \frac{\partial E_x}{\partial z}-\frac{\partial E_z}{\partial x} = -\frac{\partial B_y}{\partial t} }$$ $$\large{ \frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y} = -\frac{\partial B_z}{\partial t} }$$

上式に、$\large{\boldsymbol{E} =(E_x\hspace{1pt},\hspace{1pt}E_y\hspace{1pt},\hspace{1pt}E_z)= (E_{x0} \cos(kz-\omega t) , 0, 0)}$ を代入します。 $$\large{ 0 = -\frac{\partial B_x}{\partial t} }$$ $$\large{ \frac{\partial E_x}{\partial z}= -\frac{\partial B_y}{\partial t} }$$ $$\large{ 0 = -\frac{\partial B_z}{\partial t} }$$

上式から、磁場$\large{\boldsymbol{B}}$ は $\large{x\hspace{1pt}}$方向、$\large{z\hspace{1pt}}$方向には時間変化せず、$\large{y\hspace{1pt}}$方向のみに振動することか分かります。
このとき磁場の $\large{y\hspace{1pt}}$成分$\large{B_y}$ を求めると、以下のように計算されます。 $$\large{ \frac{\partial E_x}{\partial z}= -\frac{\partial B_y}{\partial t} }$$ 上式に $\large{E_x = E_{x0} \cos(kz-\omega t) }$ を代入すると、以下のようになります。 $$\large{ \frac{\partial}{\partial z}(E_{x0} \cos(kz-\omega t) )= -\frac{\partial B_y}{\partial t} }$$ $$\large{k E_{x0} \sin(kz-\omega t) = \frac{\partial B_y}{\partial t}}$$ 両辺を $\large{t}$ で積分すると以下のようになります。(積分定数は時間に依存しないため、振動には寄与しないと考えて $\large{0}$ としています。) $$\large{\displaystyle \int k E_{x0} \sin(kz-\omega t) dt = B_y}$$ $$\large{ \frac{k}{\omega} E_{x0} \cos(kz-\omega t) = B_y}$$ 真空中の分散関係 (波数$\large{k}$ と角周波数$\large{\omega}$ の関係式)から、$\large{\omega = ck}$ であるため、以下のようになります。 $$\large{ E_{x0} \cos(kz-\omega t) = cB_y}$$ すなわち、$\large{E_{x0}\cos(kz-\omega t) = E_x}$ から $$\large{ E_x = cB_y}$$ 以上より、$\large{z\hspace{2pt}}$方向に進行する電場$\large{\boldsymbol{E}}$ が $\large{x\hspace{2pt}}$方向にみに振動しているときは、磁場$\large{\boldsymbol{B}}$ は $\large{y\hspace{1pt}}$方向に振動することが分かります。

また、その振幅の大きさの関係は、電場の振幅を $\large{E_{x\hspace{1pt}0}}$、磁場の振幅を $\large{B_{y\hspace{1pt}0}}$ とすると、真空中の光速$\large{c}$ を用いて$\large{ E_{x\hspace{1pt}0} = c\hspace{1pt}B_{y\hspace{1pt}0}}$ となります。