二次関数と二次方程式の英語表現
本項では以下の内容を解説しています。
- ・二次関数(式とグラフ)の英語表現
- ・二次方程式(解の公式と判別式)の英語表現
- ・関連用語の一覧
【1】二次関数の英語表現
本章では、二次関数に関する英語表現について解説します。
【1-1】二次関数の式の英語表現
二次関数は英語でquadratic functionといいます。
二次関数とは、以下の式のように変数xの最大の次数が2であるような関数のことをいいます。
上記のような二次関数では、xは独立変数を意味するindependent variable、yは従属変数を意味するdependent variableともいいます。
また、二次関数のaやbは係数を意味するcoefficient、\(\hspace{1pt}\large{c}\hspace{2pt}\)は定数を意味するconstantともいいます。
例えば『\(\hspace{1pt}\large{x^2}\hspace{2pt}\)の係数はaです。』は英語で『The coefficient of x squared is a.』などといいます。
x squaredは\(\hspace{1pt}\large{x^2}\hspace{2pt}\)を表す言い方です。(べき乗の英語表現で解説しています。)
また、二次関数の式に数字を当てはめた"\(\hspace{1pt}\large{y = 3 x^2 +2x - 5}\hspace{2pt}\)"を英語で読むと
『y is equal to 3 x squared plus 2 x minus 5』といいます。
【1-2】二次関数のグラフの英語表現
二次関数のグラフは放物線を描きます。放物線は英語でparabolaといいます。
下図の左に\(\hspace{1pt}\large{a>0}\hspace{2pt}\)、右に\(\hspace{1pt}\large{a < 0}\hspace{2pt}\)のときの\(\hspace{1pt}\large{y=a x^2}\hspace{2pt}\)のグラフを示します。
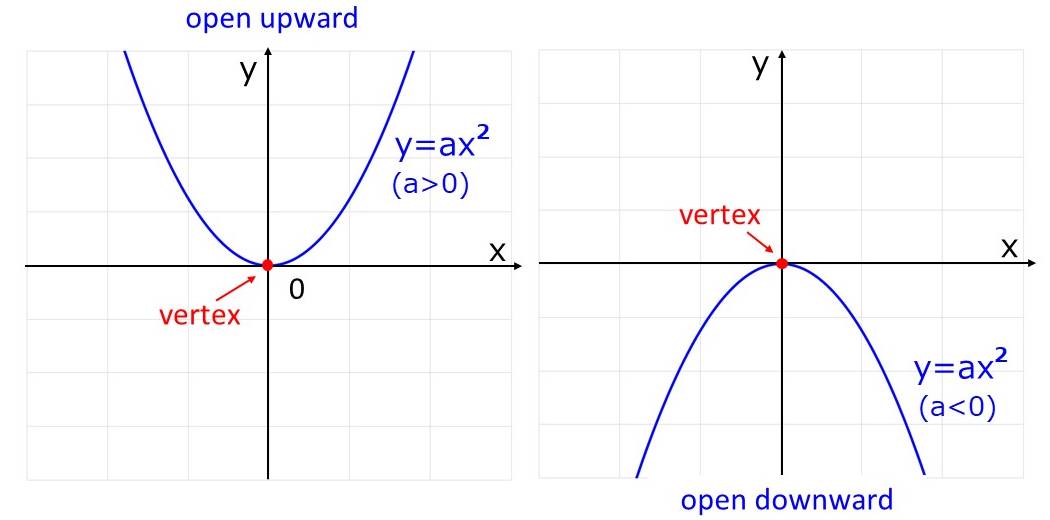
二次関数は\(\hspace{1pt}\large{a}\hspace{2pt}\)の符号により、放物線の形状が大きく2種類に分類されます。
\(\hspace{1pt}\large{a>0}\hspace{2pt}\)の場合、図の左のように放物線は上側が開いた形状になります。日本語では、この放物線の形状を『下に凸』と表すことがありますが、英語の場合はThe parabola opens upward.といいます。
\(\hspace{1pt}\large{a < 0}\hspace{2pt}\)の場合、図の右のように放物線は下側が開いた形状になります。英語ではThe parabola opens downward.といいます。
また、放物線の頂点をvertexといいます。\(\hspace{1pt}\large{a>0}\hspace{2pt}\)の場合は頂点が最小値(minimum value)、\(\hspace{1pt}\large{a < 0}\hspace{2pt}\)の場合は頂点が最大値(maximum value)になります。
【2】二次方程式の英語表現
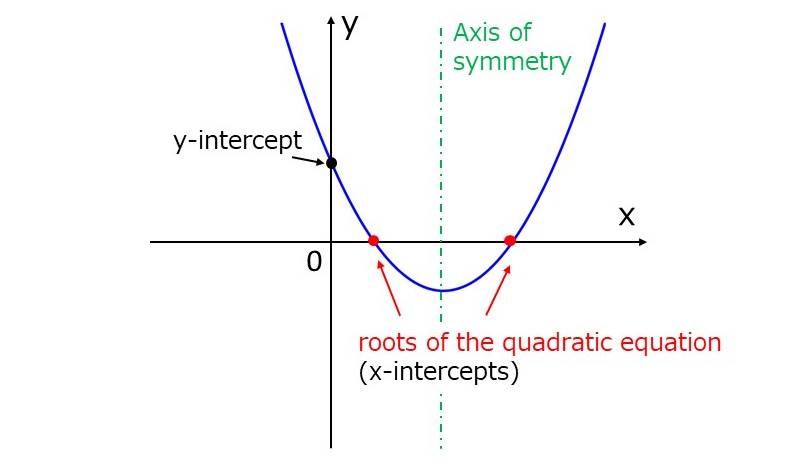
下図のような二次関数の放物線が、x軸と交わる場合について考えます。
このとき、x軸との交点の座標は、二次関数が\(\hspace{1pt}\large{y=0}\hspace{2pt}\)であるときに与えられるので、\(\hspace{1pt}\large{a x^2 + bx +c = 0}\hspace{2pt}\)の解により求められます。
二次関数\(\hspace{1pt}\large{y = a x^2 + bx +c}\hspace{2pt}\)において、\(\hspace{1pt}\large{y=0}\hspace{2pt}\)の式を二次方程式といい、英語ではquadratic equationといいます。
【2-1】二次方程式の解の英語表現
二次方程式の解を英語でrootsといいます。 二次方程式の解は、roots of the quadratic equationと表されます。
また、切片を意味するinterceptから、二次方程式の解をx-interceptsと言う場合もあります。
ここで、\(\hspace{1pt}\large{y=x^2 - 4x +3}\hspace{2pt}\)は因数分解(factorization)すると、\(\hspace{1pt}\large{y=(x-1)(x-3)}\hspace{2pt}\)となることから、\(\hspace{1pt}\large{y=0}\hspace{2pt}\)の解は\(\hspace{1pt}\large{x=1,3}\hspace{2pt}\)であることが分かります。
\(\hspace{1pt}\large{y=(x-1)(x-3)}\hspace{2pt}\)は英語で『y is equal to x minus 1 times x minus 3』といいます。
また、『二次方程式の解はx=1とx=3です。』は英語で『The roots of the quadratic equation are x = 1 and x = 3.』といいます。
二次関数のグラフは、頂点を通り、y軸と水平な直線に対して対称となります。この直線をaxis of symmetryといいます。
【2-2】解の公式の英語表現
二次方程式の解の公式を英語ではquadratic formulaといいます。
二次方程式が以下の式であるとします。 $$\large{a x^2 + bx +c = 0\hspace{10pt}(a \neq 0)}$$ このとき、解の公式は以下のようになります。 $$\large{x = \frac{-b \pm \sqrt{b^2 -4 ac}}{2a}}$$
解の公式\(\hspace{1pt}\large{x = \frac{-b \pm \sqrt{b^2 -4 ac}}{2a}}\hspace{2pt}\)は英語で表すと、"x is equal to negative b plus or minus the square root of b squared minus 4ac, (all) divided by 2a"といいます。
"A divided by B"は、分数\(\hspace{1pt}\Large{\frac{A}{B}}\hspace{2pt}\)を表す表現です。"all divided by"は分子に複数の項を持つ分数に対して使われる表現で、『(分子の)全体を割る』という意味で使われることがあります。
(分数の英語表現は別ページに解説しています。)
また、『解の公式は二次方程式の解を求めるために使用されます。』を英語で説明すると、以下のようになります。
『Quadratic formula is used to find roots of the quadratic equation.』
【2-3】判別式の英語表現
解の公式中の\(\hspace{1pt}\large{b^2 -4 ac}\hspace{2pt}\)の項を判別式といい、英語ではdiscriminantといいます。
判別式はdiscriminantの頭文字を取って、\(\hspace{1pt}\large{D=b^2 -4 ac}\hspace{2pt}\)と表記します。

判別式\(\hspace{1pt}\large{D}\hspace{2pt}\)を計算することで、二次方程式の解の個数を求めることができます。
判別式\(\hspace{1pt}\large{D}\hspace{2pt}\)が0より大きいとき、二次方程式は2つの異なる実数解を持ちます。英語では実数解をreal rootといいます。
判別式\(\hspace{1pt}\large{D}\hspace{2pt}\)が0と等しいとき、二次関数はx軸と接するため、1つの重解を持ちます。
また、判別式\(\hspace{1pt}\large{D}\hspace{2pt}\)が0より小さい場合は、二次方程式は解を持ちません。解の範囲を複素数まで考えると、解を導くことができます。解が複素数である場合、imaginary rootやcomplex rootなどといいます。
『判別式によって、二次方程式の解の個数を求めることができます。』を英語で表すと、
『Discriminant determines the number of roots of a quadratic equation.』
【3】二次関数と二次方程式の英語の用語
二次関数に関する英語の用語を以下の表にまとめています。
| 用語 | 意味 |
|---|---|
| quadratic function | ・二次関数 |
| coefficient | ・係数 |
| constant | ・定数 |
| variable | ・変数 |
| independent variable | ・独立変数 |
| dependent variable | ・従属変数 |
次に、二次関数のグラフに関する用語を表にまとめています。
| 用語 | 意味 |
|---|---|
| vertex | ・頂点 |
| parabola | ・放物線 |
| maximum value | ・最大値 |
| minimum value | ・最小値 |
| horizontal axis | ・水平軸 |
| vertical axis | ・垂直軸 |
| x axis | ・x軸 |
| y axis | ・y軸 |
| xy plain | ・xy平面 |
| x-intercept | ・x切片(y=0のときのx) |
| y-intercept | ・y切片(x=0のときのy) |
次に、二次方程式に関する用語をまとめています。
| 用語 | 意味 |
|---|---|
| quadratic equation | ・二次方程式 |
| factorization | ・因数分解 |
| quadratic formula | ・解の公式 |
| discriminant | ・判別式 |
| real root | ・実数解 |
| imaginary root | ・虚数解 |