対数の英語表現
本項では以下の内容を解説しています。
- ・対数の式の英語表現
- ・自然対数、常用対数の英語表現
- ・関連用語の一覧
【1】対数の英語表現
対数を英語でlogarithmといいます。
また、対数を関数で表した対数関数をlogarithm functionもしくは、logarithmic functionといいます。
本項では、対数の式や、常用対数、自然対数などの英語表現について解説します。
【1-1】対数の式の英語表現
べき乗は、ある数を複数回かけ合わせた計算を表します。例えば、\(\hspace{1pt}\large{2^3=2 \times 2 \times 2 = 8}\hspace{2pt}\)では、2を3回かけると8になることを表します。
一方、対数による表記では\(\hspace{1pt}\large{2^3= 8}\hspace{2pt}\)を、\(\hspace{1pt}\large{\log_2 8 =3}\hspace{2pt}\)と表記し、2を何乗すると8となるかを表します。
\(\hspace{1pt}\large{\log_2 8 =3}\hspace{2pt}\)の場合、2を底(base)、8を真数(Argument)、3を指数(exponent)といいます。
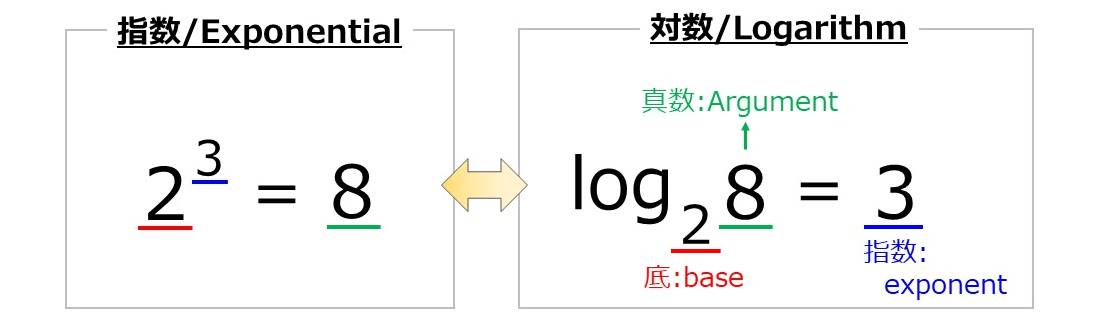
対数の数式を英語で言い表すときは、logarithmを省略した、logを使用します。底がa,真数がbであるときの対数(\(\hspace{1pt}\large{\log_a b}\hspace{2pt}\))は、"Log base a of b"といいます。
例えば、『\(\hspace{1pt}\large{\log_2 8 =3}\hspace{2pt}\)』を英語で言い表すと"Log base 2 of 8 is equal to 3."となります。
また、『\(\hspace{1pt}\large{y = \log_2 x^3}\hspace{2pt}\)』を英語で言い表すと"y is equal to log base 2 of x to the 3."となります。
(\(\hspace{1pt}\large{x^3}\hspace{2pt}\)は、『x (raised) to the (power of) 3』 と言い表します。詳しくはべき乗のページで解説しています。)
【1-2】よく使用される対数の形式
よく使われる対数として、底にネイピア数を使用する自然対数(natural logarithm)、底に10を使用する常用対数(common logarithm)、底に2を使用する二進対数(binary logarithm)などがあります。
| 日本語 | 英語 | 数式 |
|---|---|---|
| 自然対数 | natural logarithm | \(\hspace{1pt}\large{\log_{e}X ~ (=ln X)}\hspace{2pt}\) |
| 常用対数 | common logarithm | \(\hspace{1pt}\large{\log_{10}X ~ (=\log X)}\hspace{2pt}\) |
| 二進対数 | binary logarithm | \(\hspace{1pt}\large{\log_{2}X}\hspace{2pt}\) |
本ページでは、自然対数と常用対数を取り上げて解説しています。
【2】自然対数の英語表現
底が\(\hspace{1pt}\large{e}\hspace{2pt}\)の対数を、特別に自然対数といいます。英語では、natural logarithmといいます。
\(\hspace{1pt}\large{e}\hspace{2pt}\)は、\(\hspace{1pt}\large{e=2.718 \cdots}\hspace{2pt}\)と続く値を持ちます。日本語では、\(\hspace{1pt}\large{e}\hspace{2pt}\)を『ネイピア数』や『自然対数の底』という言い方をします。 一方、英語ではEuler's numberという言い方が一般的です。
自然対数をそのまま記述すると、『\(\hspace{1pt}\large{\log_{e}2}\hspace{2pt}\)』などとなりますが、\(\hspace{1pt}\large{log}\hspace{2pt}\)の代わりに\(\hspace{1pt}\large{ln}\hspace{2pt}\)を使用して『\(\hspace{1pt}\large{\ln 2}\hspace{2pt}\)』とも書かれます。
ここで、『自然対数は\(\hspace{1pt}\large{e}\hspace{2pt}\)を底に持ちます。』を英語で言い表すと"Natural log has base e (Euler's number)."となります。
また、『自然対数\(\hspace{1pt}\large{\ln x}\hspace{2pt}\)の逆関数は、指数関数\(\hspace{1pt}\large{e^x}\hspace{2pt}\)です。』を英語で言い表すと"The inverse function of natural logarithm \(\hspace{1pt}\large{\ln x}\hspace{2pt}\) is exponential function \(\hspace{1pt}\large{e^x}\hspace{2pt}\)."となります。
【3】常用対数の英語表現
底が10の対数を、特別に常用対数といいます。英語では、common logarithmといいます。
常用対数は、真数が10の何乗かを表すため、桁が大きく変化する数値どうしを比較する目的でよく使用されます。
例えば、『\(\hspace{1pt}\large{\log_{10}1000}\hspace{2pt}\)』は常用対数であり、\(\hspace{1pt}\large{1000=10^3}\hspace{2pt}\)であることから、\(\hspace{1pt}\large{\log_{10}1000=\log_{10}10^3=3}\hspace{2pt}\)となります。
常用対数では、底の10を省略して書き表す場合があります。例えば、『\(\hspace{1pt}\large{\log_{10}100}\hspace{2pt}\)』の底の10を省略し、『\(\hspace{1pt}\large{\log 100}\hspace{2pt}\)』と書くことがあります。
ここで、『底の値が書かれていない対数は、底が10であることを意味します。』を英語で言い表すと"If no base is written for logarithm, the base is assumed to be 10."となります。
【補足】常用対数の用語 | 桁数の求め方
常用対数によく使用される英語の用語として、桁数に関連した用語があります。これらの用語は、常用対数により桁数を求める計算の過程で出てくるため、べき乗の桁数を求める方法を紹介します。
ある正の数\(\hspace{1pt}\large{X}\hspace{2pt}\)は\(\hspace{1pt}\large{1 \leq a < 10}\hspace{2pt}\)を使用して、以下のように書き表せます。 $$\large{X = a \times 10^n \ \rm{(ただし、nは整数)}}$$
例えば、\(\hspace{1pt}\large{X=102.5}\hspace{2pt}\)である場合、\(\hspace{1pt}\large{X=1.025 \times 10^2}\hspace{2pt}\)と表すことができます。
ここで、\(\hspace{1pt}\large{X}\hspace{2pt}\)の常用対数(\(\hspace{1pt}\large{\log_{10}X}\hspace{2pt}\))を計算すると、以下のように変形できます。
このとき、\(\hspace{1pt}\large{n}\hspace{2pt}\)を指標(characteristic)、\(\hspace{1pt}\large{\log_{10}a}\hspace{2pt}\)を仮数(mantissa)といいます。
\(\hspace{1pt}\large{\log_{10}a}\hspace{2pt}\)は、常用対数表(table of common logarithms)という表から数値を読み取ることかできます。
ここで、\(\hspace{1pt}\large{1 \leq a < 10}\hspace{2pt}\)であることから、\(\hspace{1pt}\large{0 \leq \log_{10}a < 1}\hspace{2pt}\)となります。
したがって、\(\hspace{1pt}\large{\log_{10}X}\hspace{2pt}\)の整数部分が、\(\hspace{1pt}\large{X}\hspace{2pt}\)の指標\(\hspace{1pt}\large{n}\hspace{2pt}\)となるため、\(\hspace{1pt}\large{X}\hspace{2pt}\)の桁数を求めることができます。
例えば、\(\hspace{1pt}\large{X=2^{100}}\hspace{2pt}\)の桁数を求める場合、常用対数表から\(\hspace{1pt}\large{\log_{10}{2}=0.3010 \cdots}\hspace{2pt}\)であることを用いると、以下のように求められます。 $$\large{\log_{10} 2^{100} = 100 \log_{10}{2} = 30 + 0.10 \cdots}$$
つまり、\(\hspace{1pt}\large{\log_{10} 2^{100}}\hspace{2pt}\)の指標は\(\hspace{1pt}\large{n=30}\hspace{2pt}\)であることが分かります。
したがって、\(\hspace{1pt}\large{2^{100}}\hspace{2pt}\)は以下の式を満たします。
$$\large{10^{30} < 2^{100} < 10^{31}}$$
以上から、\(\hspace{1pt}\large{X=2^{100}}\hspace{2pt}\)の桁数が31桁であることが分かります。
ここで、『Xの常用対数の値が1から2の間であるとき、Xは2桁の数字です。』を英語で言い表すと"If common log of X lies between 1 and 2, the number of digits of X is 2."となります。
【4】対数の英語用語のまとめ
対数の数式に関する英語表現の用語の一覧を示します。
| 用語 | 意味 |
|---|---|
| logarithm | ・対数 |
| logarithmic function | ・対数関数 |
| logarithmic equation | ・対数方程式 |
| base | ・(対数の)底 |
| argument | ・(対数の)真数 |
| exponent | ・指数 |
自然対数に関する英語表現の用語の一覧を示します。
| 用語 | 意味 |
|---|---|
| natural logarithm | ・自然対数 |
| Euler's number | ・ネイピア数 |
| inverse function | ・逆関数 |
| exponential function | ・指数関数 |
常用対数に関する英語表現の用語の一覧を示します。
| 用語 | 意味 |
|---|---|
| common logarithm | ・常用対数 |
| table of common logarithms | ・常用対数表 |
| characteristic | ・(常用対数の)指標 |
| mantissa | ・(常用対数の)仮数 |
| the number of digits | ・桁数 |
その他、対数に関する英語表現の用語の一覧を示します。
| 用語 | 意味 |
|---|---|
| binary logarithm | ・二進対数 |
| semilog graph | ・片対数グラフ |
| log-log graph | ・両対数グラフ |
| Logarithmic scale | ・対数スケール |
| change of base formula | ・底の変換公式 |