位相速度と群速度

本項では、光の位相速度や群速度、その性質について解説します。

【1】位相速度とは

位相速度(英:phase velocity)とは、正弦波の波形の山や谷が伝搬する速さのことを言います。

図1に、時刻 \(\large{t=0}\) から時間 \(\large{Δt}\) だけ経過し、正弦波が \(\large{\Delta x}\) だけ進行した様子を示します。

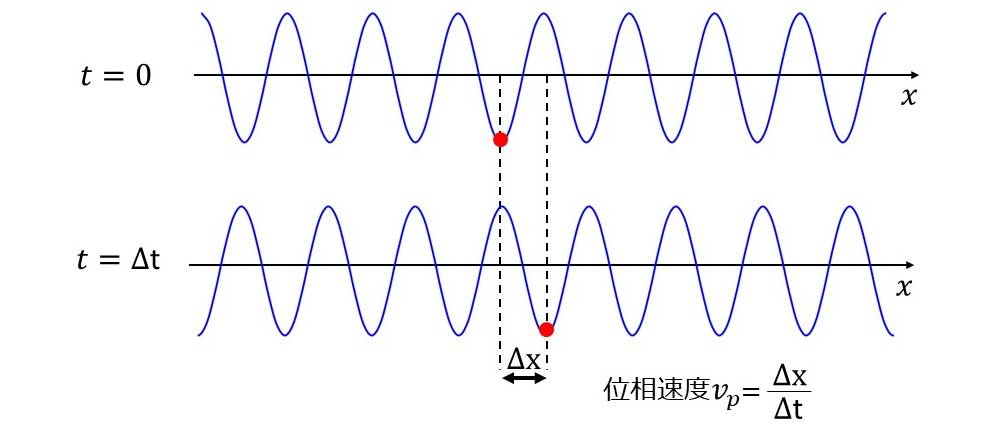
位相速度\(\large{v_p}\) は、ある時間 \(\large{\Delta t}\) の間に波形が進む距離 \(\large{\Delta x}\) であるため、以下のように書き表せます。 $$\large{v_p = \frac{\Delta x}{\Delta t}\hspace{10pt}(1)}$$

【1-1】位相速度の式

波数\(\large{k}\)、角周波数\(\large{\omega}\) で進行する正弦波 \(\large{A \cos (kz - \omega t)}\) の位相速度の式を導出します。

正弦波は周期\(\large{T}\) の時間で 1波長\(\large{\lambda}\) だけ進行するため、(1)式より位相速度は以下のようになります。 $$\large{v_p = \frac{\lambda}{T}}$$ 波長\(\large{\lambda}\) と波数\(\large{k}\) の関係は\(\displaystyle\large{\lambda=\frac{2 \pi}{k}}\)、周期\(\large{T}\) と角周波数\(\large{\omega}\) の関係は \(\displaystyle\large{T=\frac{2 \pi}{\omega}}\) となります。したがって、以下の位相速度の式が求められます。

【1-2】光の位相速度

電磁気学では、光は電場と磁場が垂直に振動する横波として記述されます。図2に、x軸上で電場と磁場が振動する様子を図示します。

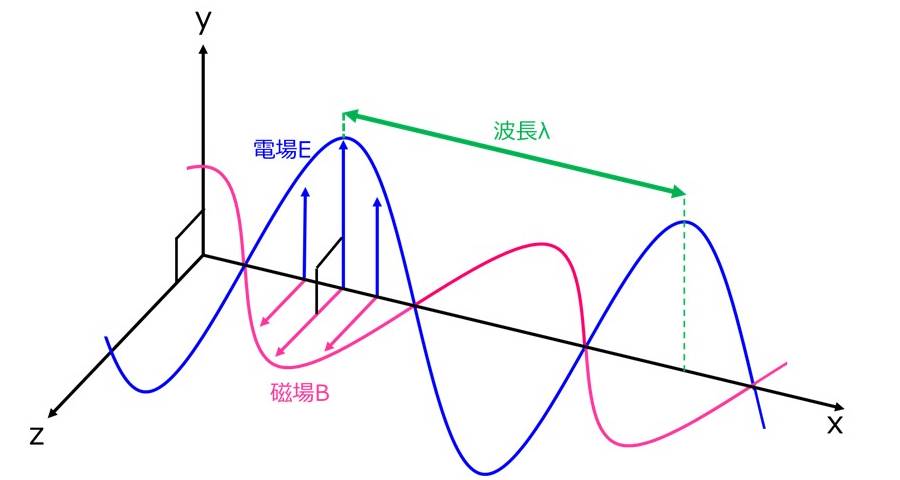
図2に示すように、光は電場と磁場が正弦波として伝わる波であり、式(1)の位相速度が定義されます。

屈折率\(\large{n}\) の物質中を進む光の位相速度\(\large{v_p}\) は、真空中の光速\(\large{c}\) と屈折率\(\large{n}\) によって以下の関係になります。 $$\large{v_p = \frac{c}{n}=\frac{\omega}{k}}$$

真空中では、屈折率\(\large{n}\) は1であるため、光の位相速度\(\large{v_p}\) は光速と等しくなります。

一方、物質中を伝搬する光の位相速度は、物質の屈折率\(\large{n}\) に依存して変化します。 よく知られているように、ガラスのような透明な物質では、可視光の領域で波長が長いほど屈折率が小さいという性質があります。 したがって、ガラス中を伝搬する可視光は、波長が長いほど、位相速度\(\large{v_p}\) は大きくなります。

【2】群速度とは

群速度(英:group velocity) とは、振動数の異なる波が重なった波束が進行する速さのことをいいます。
波の波数を \(\large{k}\)、角周波数を \(\large{\omega}\) とすると、群速度は \(\displaystyle\large{\frac{d \omega}{d k}}\) により表されます。

【2-1】群速度の式

波数\(\large{k}\) と角周波数\(\large{\omega}\) がわずかに異なる2つの正弦波が重なる場合について考えます。

波数\(\large{k}\)、角周波数\(\large{\omega}\)、振幅\(\large{A}\) の正弦波がx軸の正の方向に伝搬しているとき、波の式は以下のように書き表せます。 $$\large{f(x,t)=A \cos(kx-\omega t)}$$

上式から、波数が \(\large{\Delta k}\)、角周波数が \(\large{\Delta \omega}\) だけ異なる2つの正弦波が、以下の式で表されるとします。 $$\large{f_1(x,t)=A \cos((k+\Delta k)x-(\omega+\Delta \omega)t)}$$ $$\large{f_2(x,t)=A \cos((k-\Delta k)x-(\omega-\Delta \omega)t)}$$

この2式を足し合わせた合成波 \(\large{f_1 + f_2}\) を計算すると、三角関数の和積の公式から以下のように求められます。 $$\large{f_1 + f_2 = 2A \cos(kx -\omega t)\cos(\Delta kx - \Delta \omega t )\hspace{20pt}(3)}$$

この合成波の式(3)をグラフにしたものを以下の図1に示します。

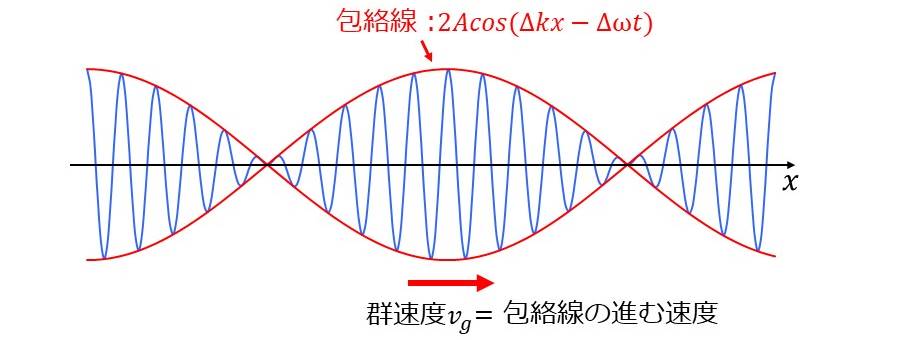
図中の青線が式(1)の合成波\(\large{f_1 + f_2}\) の形状を表します。一方、図中の赤線は合成波の包絡線を表します。 このとき、包絡線の形状は、式(3)中の \(\large{2A \cos(\Delta kx - \Delta \omega t )}\) となります。

群速度とは、この包絡線が伝搬する速度を表しています。(3)式の包絡線の伝わる群速度\(\large{v_g}\) を \(\large{\Delta k}\)、\(\large{\Delta \omega}\) により表すと以下のようになります。 $$\large{v_g = \frac{\Delta \omega}{\Delta k}}$$ 上式の \(\large{\Delta k \rightarrow 0}\) の極限が群速度\(\large{v_g}\) の式となります。 $$\large{v_g = \frac{d \omega}{d k}}$$

【2-2】真空中の光の群速度

真空中では、角周波数と波数には \(\large{\omega = c k}\) の関係があります。つまり、真空中では角周波数と波数は単純な比例関係にあることを意味します。

この場合、位相速度\(\large{v_p}\) は波長(波数)に依存せず 光速\(\large{c}\) に一定となります。このような関係を『分散がない』という言い方をします。

また、このときの群速度を \(\displaystyle\large{v_g = \frac{d \omega}{d k}}\) により計算すると、真空中の光速\(\large{c}\) に等しくなります、 $$\large{v_g = \frac{d \omega}{d k} = c}$$ したがって、真空中では、位相速度\(\large{v_p}\) と群速度\(\large{v_g}\) は真空中の光速に等しくなります。

【2-3】物質中の光の群速度

光が物質中を伝搬する場合、物質の屈折率\(\large{n}\) は波長(波数)に依存して変化します。
つまり、位相速度 \(\displaystyle\large{v_p=\frac{c}{n}}\) は波長(波数)に依存して変化します。このような関係を『分散がある』という言い方をします。

分散のある物質中では、\(\displaystyle\large{\omega=\frac{c k}{n}}\)であることから、群速度\(\large{v_g}\) は以下のような計算式で表されます。 $$\large{v_g = \frac{d \omega}{d k} = \frac{d}{d k}\frac{kc}{n}=\frac{c}{n}-\frac{ck}{n^2}\frac{dn}{dk}=v_p\left(1-\frac{k}{n}\frac{dn}{dk}\right)}$$

また、別の計算式として群速度\(\large{v_g}\) は以下のように表すこともできます。
\(\displaystyle\large{v_g = \frac{d \omega}{d k}}\) の両辺の逆数を考えると、逆関数の微分公式から以下の式を導出できます。 $$\large{\frac{1}{v_g} = \frac{1}{\frac{d \omega}{d k}}=\frac{dk}{d\omega}=\frac{1}{c}\left(n + \frac{d n}{d \omega} \omega \right)}$$ したがって、群速度\(\large{v_g}\) は以下のようにも計算できます。 $$\large{ \displaystyle v_g = \frac{v_p}{1 + \frac{\omega}{n}\frac{d n}{d \omega}}\hspace{20pt}(4)}$$

ガラスなどの透明な物質は、可視光の波長域では角周波数\(\large{\omega}\)が増加すると、屈折率\(\large{n}\)が増加する関係にあります。 このような関係にある\(\large{\omega}\)の領域を正常分散といいます。

したがって、正常分散の領域では\(\displaystyle\large{\frac{d n}{d \omega}>0}\) であるため、(4)式より群速度\(\large{v_g}\) は位相速度\(\large{v_p}\) より常に小さい関係にあります。

【2-4】位相速度と群速度の違い

位相速度と群速度の違いは、位相速度は 『ある1つの周波数の波の位相が伝わる速さ』を表し、群速度は 『複数の周波数からなる波の束(包絡線)が進む速度』を表している点にあります。

厳密には、位相速度は波の始まりや終わりが存在しない無限に連続する正弦波の位相の伝わる速さを意味します。
この理想的な正弦波は、一定の山と谷が繰り返されるだけなので、エネルギーを伝達することができず、信号として情報を伝えることはできません。

一方、群速度は異なる周波数を持った正弦波が重ね合わさった波束が伝わる速度を表します。
波束は、複数の波が重なり干渉することで、振動のエネルギーの強い部分と弱い部分が存在します。つまり、波束は光の信号として情報を送ることができます。
そのため、群速度はエネルギー(信号)が伝搬する速度と考えることができます。

例えば、光ファイバーを伝わる信号は、パルス(光の波束)の状態で伝送されます。パルスによって信号が伝わる速さは群速度により表されます。

参考文献

---