単レンズの焦点距離, 主点, 体積の計算ツール
単レンズの 曲率半径, 厚み, 屈折率, 外径 から 焦点距離, 主点位置, 体積 などを求める計算ツールです。
単レンズの計算ツール
【レンズ形状の設定】
第1面 曲率半径[mm]
第2面 曲率半径[mm]
レンズの厚み[mm]
屈折率
外径[mm]
密度[g/cm3]
・曲率半径は左側に凸が正、右側に凸が負
(例)両凸レンズ : 第1面 正、第2面 負
・平面は曲率半径を "0" と入力
・外径,密度 は 体積,質量 の計算のみに使用
【出力の設定】
出力値の小数点以下の桁数
| 焦点距離\(\hspace{2pt}\large{f}\hspace{2pt}\) | 像側主点位置\(\hspace{2pt}\large{\Delta'}\hspace{2pt}\) |
|---|---|
| 物体側主点位置\(\hspace{2pt}\large{\Delta}\hspace{2pt}\) | バックフォーカス\(\hspace{2pt}\large{f_b}\hspace{2pt}\) |
|---|---|
| 体積 | 質量 |
|---|---|
(※当サイトの提供する計算結果や情報については一切責任は負いません。)
【1】入力値の意味と符号関係
計算ツールに入力する値の意味や符号について解説します。
【曲率半径 \(\hspace{2pt}\large{R}\hspace{2pt}\) 】
曲率半径\(\hspace{2pt}\large{R_1, R_2}\hspace{2pt}\) は球面の曲がり具合を表現する値です。
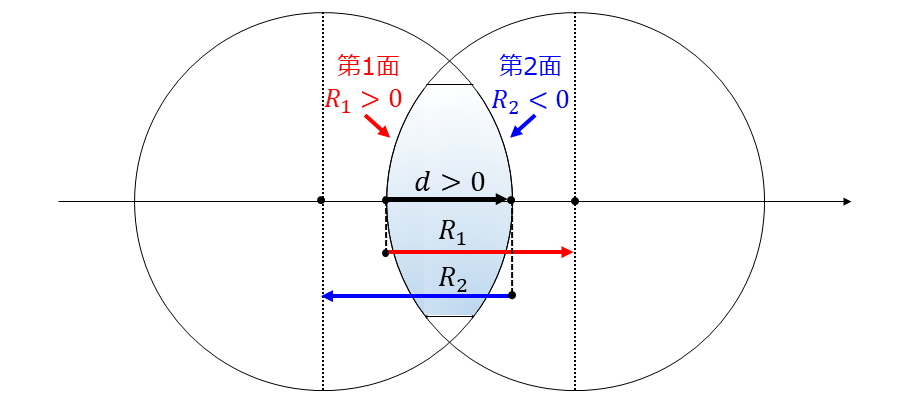
光軸 (下図のレンズ中心を通る軸) 上において、物体側(左側)の球面を第1面、像側(右側)を第2面としたとき、第1面の曲率半径を\(\hspace{2pt}\large{R_1}\hspace{2pt}\)、第2面の曲率半径を\(\hspace{2pt}\large{R_2}\hspace{2pt}\)とします。
このとき、曲率半径\(\hspace{2pt}\large{R_1, R_2}\hspace{2pt}\) は 球面の頂点 から 中心 までの距離で定義されます。また、曲率半径の符号は、球面の頂点から中心に向かって線を引いたときに、右向きが正と定義します。
例えば、図1に示すように両凸レンズの場合は、第1面の曲率半径 \(\hspace{2pt}\large{R_1}\hspace{2pt}\) は正、第2面の曲率半径 \(\hspace{2pt}\large{R_2}\hspace{2pt}\) は負 となります。
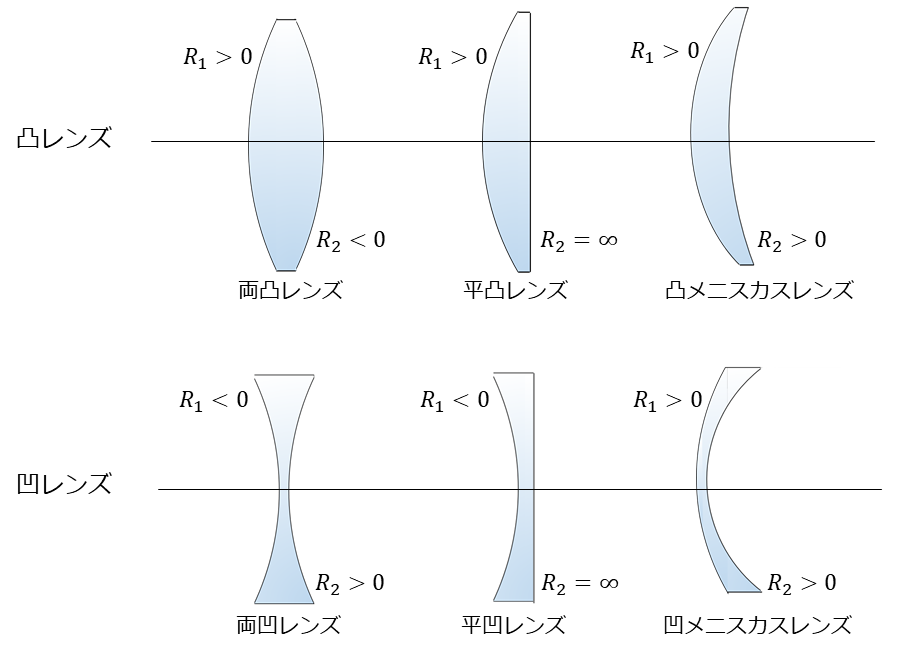
また、球面レンズの種類ごとの曲率半径の符号は以下のようになります。
平面は以下の図2のように曲率半径が無限となりますが、計算ツールに入力する場合は "0" と入力してください。
【レンズの厚み \(\hspace{2pt}\large{d}\hspace{2pt}\) 】
レンズの厚みは光軸上での球面の間隔を意味します。レンズの厚みは、正の値で入力します。
【屈折率 \(\hspace{2pt}\large{n}\hspace{2pt}\) 】
屈折率については別ページで解説しています。屈折率は、正の値で入力します。
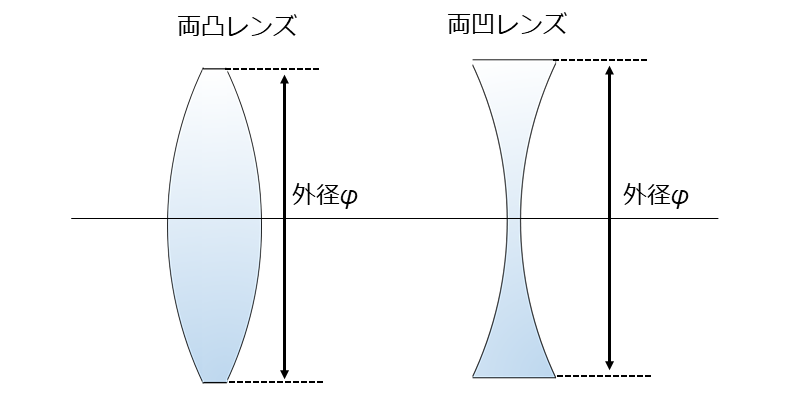
【外径 \(\hspace{2pt}\large{\phi}\hspace{2pt}\) 】
外径は以下の図3のように、レンズの外径の大きさをします。外形は、正の値で入力します。
【密度】
密度はレンズの材質の 単位立方センチメートルあたりの質量[\(\hspace{2pt}\large{g/cm^3}\hspace{2pt}\)] を入力してください。
【2】出力値の意味と符号関係
【焦点距離 \(\hspace{2pt}\large{f}\hspace{2pt}\) 】
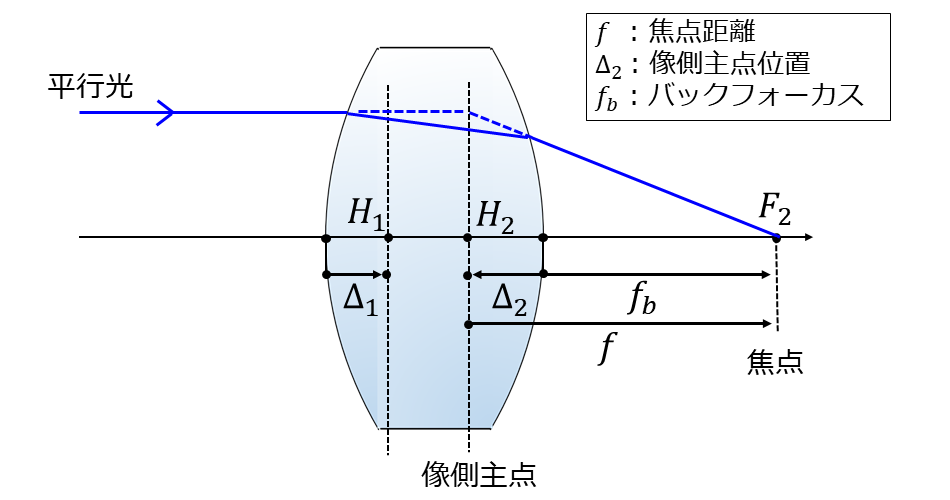
焦点距離は、以下の図4に示すように レンズに平行光を入射したときの主点\(\hspace{2pt}\large{H_2}\hspace{2pt}\) から焦点\(\hspace{2pt}\large{F_2}\hspace{2pt}\) までの距離です。
像側主点から焦点に線を引いたときに、右向きのときが正となります。例えば、図4の正レンズの焦点距離は正となります。
焦点距離\(\hspace{2pt}\large{f}\hspace{2pt}\)は、以下のレンズメーカーの公式により計算します。
\(\hspace{2pt}\large{ \displaystyle \frac{1}{f} = (N-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)}\hspace{2pt}\)
\(\hspace{2pt}\large{f}\hspace{2pt}\) : レンズの焦点距離
\(\hspace{2pt}\large{N}\hspace{2pt}\) : レンズの屈折率
\(\hspace{2pt}\large{R_1}\hspace{2pt}\) : 第1面の曲率半径
\(\hspace{2pt}\large{R_2}\hspace{2pt}\) : 第2面の曲率半径
【像側主点位置 \(\hspace{2pt}\large{\Delta_2}\hspace{2pt}\) 】
像側主点位置 \(\hspace{2pt}\large{\Delta_2}\hspace{2pt}\) は、単レンズの第2面の頂点 から主点\(\hspace{2pt}\large{H_2}\hspace{2pt}\) までの距離を表します。
レンズの第2面の頂点 から 主点\(\hspace{2pt}\large{H_2}\hspace{2pt}\) に線を引いたときに、右向きのときが正となります。
例えば、図4の正レンズの像側主点位置 \(\hspace{2pt}\large{\Delta_2}\hspace{2pt}\) は負となります。
像側主点位置 \(\hspace{2pt}\large{\Delta_2}\hspace{2pt}\) は 単レンズの近軸光線追跡の結果として計算される以下の式により計算します。
\(\hspace{2pt}\large{ \displaystyle \Delta_2 = -\frac{d}{n}\frac{n-1}{R_1}\times f}\hspace{2pt}\)
\(\hspace{2pt}\large{f}\hspace{2pt}\) : レンズの焦点距離
\(\hspace{2pt}\large{N}\hspace{2pt}\) : レンズの屈折率
\(\hspace{2pt}\large{R_1}\hspace{2pt}\) : 第1面の曲率半径
\(\hspace{2pt}\large{d}\hspace{2pt}\) : レンズの厚み
【物体側主点位置 \(\hspace{2pt}\large{\Delta_1}\hspace{2pt}\) 】
また、物体側主点位置\(\hspace{2pt}\large{\Delta_1}\hspace{2pt}\) とは、図4の像側(右側)から平行光を入射したときの、単レンズの第1面の頂点 から 主点\(\hspace{2pt}\large{H_1}\hspace{2pt}\) までの距離を表します。
レンズの第1面から 主点\(\hspace{2pt}\large{H_1}\hspace{2pt}\) に線を引いたときに、右向きのときが正となります。例えば、図4の正レンズの物体側主点位置 \(\hspace{2pt}\large{\Delta_1}\hspace{2pt}\) は正となります。
物体側主点位置\(\hspace{2pt}\large{\Delta_1}\hspace{2pt}\) は 単レンズの近軸光線追跡の結果として計算される以下の式により計算します。
\(\hspace{2pt}\large{ \displaystyle \Delta_1 = \frac{d}{n}\frac{1-n}{R_2}\times f}\hspace{2pt}\)
\(\hspace{2pt}\large{f}\hspace{2pt}\) : レンズの焦点距離
\(\hspace{2pt}\large{N}\hspace{2pt}\) : レンズの屈折率
\(\hspace{2pt}\large{R_2}\hspace{2pt}\) : 第2面の曲率半径
\(\hspace{2pt}\large{d}\hspace{2pt}\) : レンズの厚み
【バックフォーカス \(\hspace{2pt}\large{f_b}\hspace{2pt}\) 】
バックフォーカス \(\hspace{2pt}\large{f_b}\hspace{2pt}\) は、物体側(左側)から平行光が入射したときの、レンズの第2面の頂点 から 焦点\(\hspace{2pt}\large{F_2}\hspace{2pt}\) までの距離を意味します。
レンズの第2面の頂点 から 焦点\(\hspace{2pt}\large{F_2}\hspace{2pt}\) に線を引いたときに、右向きのときが正となります。
例えば、図4の正レンズのバックフォーカス \(\hspace{2pt}\large{f_b}\hspace{2pt}\) は正となります。
バックフォーカス \(\hspace{2pt}\large{f_b}\hspace{2pt}\) は、図4より以下の式により計算されます。
\(\hspace{2pt}\large{ \displaystyle f_b = f + \Delta_2}\hspace{2pt}\)
\(\hspace{2pt}\large{f}\hspace{2pt}\) : レンズの焦点距離
\(\hspace{2pt}\large{\Delta_2}\hspace{2pt}\) : 像側主点位置
【体積】
レンズの体積は、曲率半径 \(\hspace{2pt}\large{R_1,R_2}\hspace{2pt}\)、レンズの厚み \(\hspace{2pt}\large{d}\hspace{2pt}\)、外径 \(\hspace{2pt}\large{\phi}\hspace{2pt}\) によって計算します。
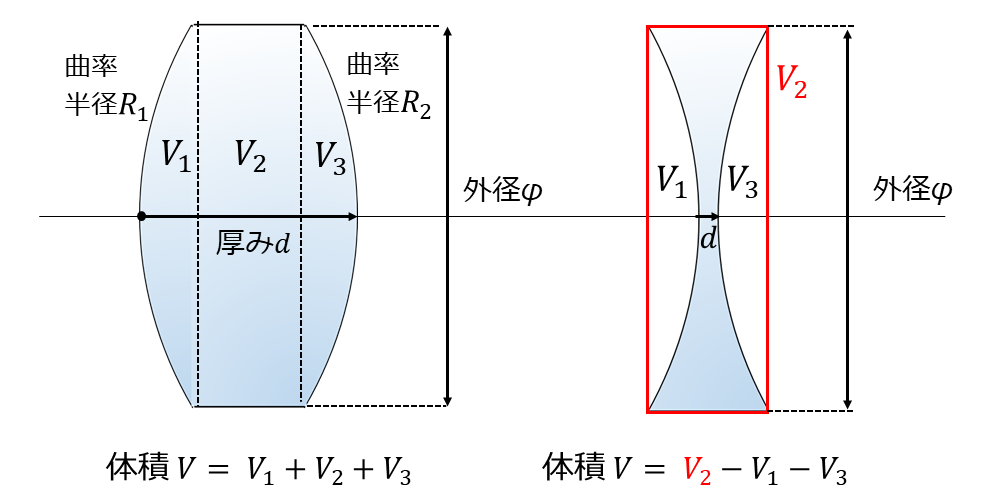
例えば、図5の両凸レンズの場合は球面の部分(\(\hspace{2pt}\large{V_1, V_3}\hspace{2pt}\))、平坦(コバ)の部分\(\hspace{2pt}\large{V_2}\hspace{2pt}\) に分割し、それぞれの部分を積分して体積を求め、足し合わせることで計算します。
また、両凹レンズの場合は球面のレンズが存在しない部分 (\(\hspace{2pt}\large{V_1, V_3}\hspace{2pt}\)) の体積、\(\hspace{2pt}\large{V_1, V_3}\hspace{2pt}\)を含んだ図5の赤枠の部分の体積 (\(\hspace{2pt}\large{V_2}\hspace{2pt}\)) を計算し、レンズの体積 \(\hspace{2pt}\large{V}\hspace{2pt}\) を \(\hspace{2pt}\large{V=V_2-V_1-V_3}\hspace{2pt}\) により求めます。
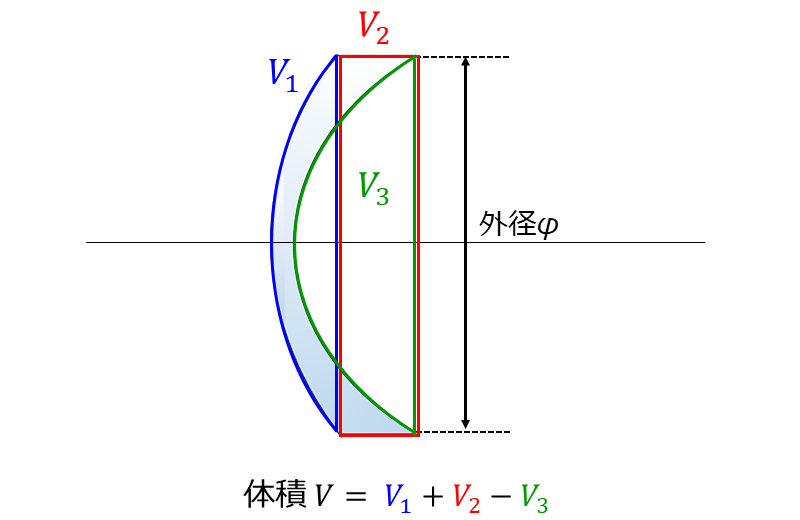
また、メニスカスレンズの場合、図6のように レンズの球面の部分 (\(\hspace{2pt}\large{V_1}\hspace{2pt}\))、\(\hspace{2pt}\large{V_3}\hspace{2pt}\)を含んだ図6の赤枠部分(\(\hspace{2pt}\large{V_2}\hspace{2pt}\))、レンズの存在しない部分 (\(\hspace{2pt}\large{V_3}\hspace{2pt}\)) の体積を求め、\(\hspace{2pt}\large{V=V_1+V_2-V_3}\hspace{2pt}\) により求めます。
本計算ツールで計算されるレンズの体積は、図5,6のように レンズの両面の球面の範囲が外径により決定されている場合について計算しています。
したがって、レンズの球面の範囲が外径によって決まっていない場合 (第1面もしくは第2面の球面の外側に平坦部が存在する場合など) については計算ができませんのでご注意ください。
【質量】
レンズの質量は、上記の体積に密度をかけることで計算します。
◆更新履歴
・計算ツール公開 (2024/1/14)