レンズメーカーの公式 | 単レンズの焦点距離
本項では、以下の内容について解説します。
- ・レンズメーカーの公式とは何か
- ・レンズメーカーの公式中の曲率半径Rや厚みdの定義
- ・レンズメーカーの公式の導出
【1】レンズメーカーの公式とは
レンズメーカーの公式(lens maker's formula)とは、単レンズの焦点距離を『屈折率\(\hspace{2pt}\large{N}\hspace{2pt}\)』、『曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)』、『厚み\(\hspace{2pt}\large{d}\hspace{2pt}\)』により計算する公式です。
レンズメーカーの公式は、以下の式により表されます。
\(\hspace{2pt}\large{f}\hspace{2pt}\) : レンズの焦点距離
\(\hspace{2pt}\large{N}\hspace{2pt}\) : レンズの屈折率
\(\hspace{2pt}\large{R_1}\hspace{2pt}\) : 第1面の曲率半径
\(\hspace{2pt}\large{R_2}\hspace{2pt}\) : 第2面の曲率半径
\(\hspace{2pt}\large{d}\hspace{2pt}\) : レンズの厚み
上式において、厚み\(\hspace{2pt}\large{d}\hspace{2pt}\)が十分に小さい(\(\hspace{2pt}\large{d=0}\hspace{2pt}\))とすることで、厚みを無視した薄肉レンズの焦点距離の公式を導くことができます。
\(\hspace{2pt}\large{ \displaystyle \frac{1}{f} = (N-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)}\hspace{2pt}\)
\(\hspace{2pt}\large{f}\hspace{2pt}\) : レンズの焦点距離
\(\hspace{2pt}\large{N}\hspace{2pt}\) : レンズの屈折率
\(\hspace{2pt}\large{R_1}\hspace{2pt}\) : 第1面の曲率半径
\(\hspace{2pt}\large{R_2}\hspace{2pt}\) : 第2面の曲率半径
レンズメーカーの公式の曲率半径と厚みの定義については本項の2章で説明しています。
また、レンズメーカーの公式の導出方法については本項の3章で説明します。
上記のレンズメーカーの公式は、当サイトで公開している【計算ツール】単レンズの焦点距離,主点,体積で計算することができます。
【2】曲率半径と厚みの定義
本章では、レンズメーカーの公式で球面レンズの形状を決定するために使用される曲率半径と厚みの定義や符号などについて解説します。
球面レンズは、2つの球面を配置した領域から形状を表現します。
例えば、両凸の球面レンズの場合、図1のように、中心が\(\hspace{2pt}\large{C_1, C_2}\hspace{2pt}\)である2つの球面を重ね合わせた領域で表現されます。
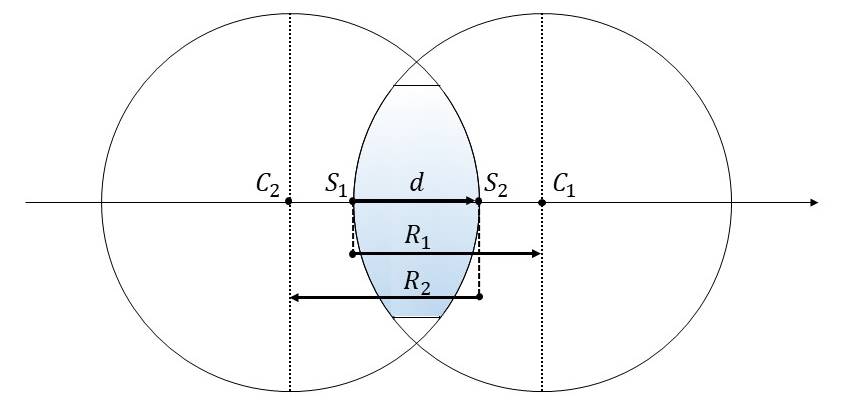
【2-1】曲率半径Rの定義と符号
\(\hspace{2pt}\large{R_1}\hspace{2pt}\)と\(\hspace{2pt}\large{R_2}\hspace{2pt}\)はそれぞれ球面レンズの第1面と第2面の曲率半径(radius of curvature)を表しています。
図中の\(\hspace{2pt}\large{S_1, S_2}\hspace{2pt}\)は球面と光軸が交わる位置であり、面頂点といいます。
曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)は面頂点\(\hspace{2pt}\large{S}\hspace{2pt}\)から球面の中心\(\hspace{2pt}\large{C}\hspace{2pt}\)までの距離で定義されます。
例えば、図1の曲率半径\(\hspace{2pt}\large{R_1}\hspace{2pt}\)は、面頂点\(\hspace{2pt}\large{S_1}\hspace{2pt}\)から球面の中心\(\hspace{2pt}\large{C_1}\hspace{2pt}\)までの光軸上の距離で表されます。
光軸の方向(右向き)を正と定義した場合、物体側(左側)に凸面を向けた面の曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)は正、像側(右側)に凸面を向けた面の曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)は負になります。
図1のような両凸レンズの各面の曲率半径の符号は、\(\hspace{2pt}\large{R_1}\hspace{2pt}\)が正、\(\hspace{2pt}\large{R_2}\hspace{2pt}\)が負の組み合わせになります。
【2-2】曲率半径Rの意味
曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)の大きさは、球面の曲がり具合を表現しています。
曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)が小さいほど、球面の曲がり具合が急であることを表します。
また、曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)の大きい方が球面は緩やかになります。曲率半径\(\hspace{2pt}\large{R}\hspace{2pt}\)を無限大まで大きくした場合(\(\hspace{2pt}\large{R=\infty}\hspace{2pt}\))が、平面に相当します。
【2-3】レンズの厚みdの定義と符号
前述したように面頂点\(\hspace{2pt}\large{S_1, S_2}\hspace{2pt}\)は球面と光軸が交わる位置を表しています。この面頂点の間隔がレンズの厚み\(\hspace{2pt}\large{d}\hspace{2pt}\)に相当します。
光軸の方向(右向き)を正と定義した場合、図1の厚み\(\hspace{2pt}\large{d}\hspace{2pt}\)は\(\hspace{2pt}\large{S_1}\hspace{2pt}\)から\(\hspace{2pt}\large{S_2}\hspace{2pt}\)までの距離のため、厚み\(\hspace{2pt}\large{d}\hspace{2pt}\)は正の値を持ちます。
【3】レンズメーカーの公式の導出
近軸光線追跡を利用して、レンズメーカーの公式を導出します。
第1面の曲率が\(\hspace{2pt}\large{R_1}\hspace{2pt}\)、第2面の曲率が\(\hspace{2pt}\large{R_2}\hspace{2pt}\)、屈折率が\(\hspace{2pt}\large{N}\hspace{2pt}\)、厚み\(\hspace{2pt}\large{d}\hspace{2pt}\)という条件で近軸追跡計算を行い、図2のような単レンズの焦点距離を計算します。
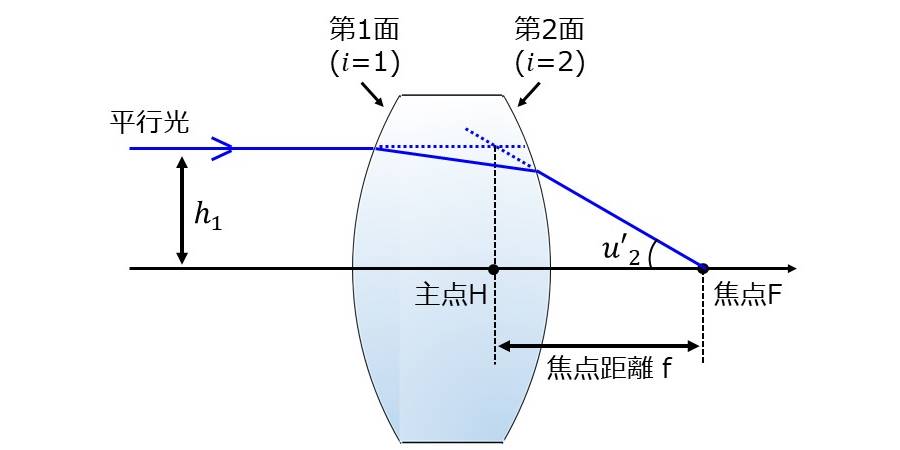
レンズの焦点距離は、主点位置\(\hspace{2pt}\large{H}\hspace{2pt}\)から焦点\(\hspace{2pt}\large{F}\hspace{2pt}\)までの距離により求められます。
図2より、焦点距離\(\hspace{2pt}\large{f}\hspace{2pt}\)は平行な近軸光線を入射したときの、入射光線の高さ\(\hspace{2pt}\large{h_1}\hspace{2pt}\)を光線角度\(\hspace{2pt}\large{u'_2}\hspace{2pt}\)で割った値で計算されます。
$$\large{f=\frac{h_1}{u'_2}}$$
近軸光線追跡による計算方法
近軸光線追跡では、光線高さ\(\hspace{2pt}\large{h}\hspace{2pt}\)と光線角度\(\hspace{2pt}\large{u}\hspace{2pt}\)を各面ごとに計算します。単レンズでは、第1面と第2面の2回の屈折を計算します。
第\(\hspace{2pt}\large{i}\hspace{2pt}\)面における屈折は以下の式により計算されます。
また、第\(\hspace{2pt}\large{i}\hspace{2pt}\)面から第\(\hspace{2pt}\large{i+1}\hspace{2pt}\)面への変換は以下の式により行います。単レンズでは、第1面から第2面への変換を行います。
\(\hspace{2pt}\large{\displaystyle h_{i+1}=h_i-d'_iu'_i}\hspace{2pt}\)
ここで、\(\hspace{2pt}\large{N}\hspace{2pt}\)は屈折率、\(\hspace{2pt}\large{R}\hspace{2pt}\)は曲率半径、\(\hspace{2pt}\large{u}\hspace{2pt}\)は近軸光線の光軸との角度を表します。
また、\(\hspace{2pt}\large{N}\hspace{2pt}\)は屈折前、\(\hspace{2pt}\large{N'}\hspace{2pt}\)は屈折後の屈折率を意味します。
第1面(i=1)の屈折の計算
第1面(i=1)の屈折は以下のように計算されます。
$$\large{N'_1 u'_1=N_1 u_1+ h_1\frac{N'_1-N_1}{R_1}}$$
ここで、焦点距離を求める場合は平行光線を入射させるため、\(\hspace{2pt}\large{u_1=0}\hspace{2pt}\)を代入します。
また、\(\hspace{2pt}\large{h_1}\hspace{2pt}\)は初期値として\(\hspace{2pt}\large{h_1=1}\hspace{2pt}\)を代入します。
入射前の媒質が空気とすると\(\hspace{2pt}\large{N_1=1}\hspace{2pt}\)、入射後の媒質が屈折率\(\hspace{2pt}\large{N}\hspace{2pt}\)とすると\(\hspace{2pt}\large{N'_1=N}\hspace{2pt}\)となります。 したがって、第1面の屈折は以下のように計算されます。 $$\large{N u'_1=\frac{N-1}{R_1}}\hspace{20pt}(1)$$
第1面から第2面への変換
次に、第1面から第2面へは以下のように変換します。 $$\large{u_2=u'_1}\hspace{40pt}(2)$$ $$\large{h_2=h_1-d_1u'_1}\hspace{8pt}(3)$$
第2面(i=2)の屈折の計算
第2面における屈折式は、以下のように計算されます。 $$\large{N'_2 u'_2=N_2 u_2+ h_2\frac{N'_2-N_2}{R_2}}$$ 第2面の屈折前の屈折率\(\hspace{2pt}\large{N_2}\hspace{2pt}\)はレンズの屈折率であるため\(\hspace{2pt}\large{N_2=N}\hspace{2pt}\)、屈折後の屈折率は空気の屈折率のため\(\hspace{2pt}\large{N'_2=1}\hspace{2pt}\)を代入します。 $$\large{u'_2=N u_2+ h_2\frac{1-N}{R_2}}\hspace{20pt}(4)$$
レンズメーカーの公式の導出(焦点距離の計算)
以上の計算の(1)~(4)式までを解くと、単レンズに平行光を入射したときの近軸光線の光線角度\(\hspace{2pt}\large{u'_2}\hspace{2pt}\)を求める式が導かれます。
焦点距離は入射光線の高さ\(\hspace{2pt}\large{h_1}\hspace{2pt}\)を光線角度\(\hspace{2pt}\large{u'_2}\hspace{2pt}\)で割った値となり、レンズメーカーの公式が導出されます。
参考文献
・(1)松居吉哉『レンズ設計法』共立出版株式会社,昭和56年10月10日 初版第4刷発行
・(2)松居吉哉『収差論』一般社団法人日本オプトメカトロニクス協会,2018年4月30日 第7刷発行