光学系の主点

本項では以下の内容を解説しています。

• ・主点の定義と作図
• ・主点位置の計算
• ・主点位置基準の結像

【1】主点とは何か

主点とは、横倍率\(\hspace{2pt}\large{\beta=+1}\hspace{2pt}\)を満たす光軸上の共役点のことをいいます。

横倍率\(\hspace{2pt}\large{\beta=+1}\hspace{2pt}\)とは、ある位置に物体を置いたときに、正立した同じ大きさの像ができることを表します。 つまり、片方の主点の位置に物体があるとき、もう片方の主点位置に正立した同じ大きさの像ができることを意味します。

また、共役点は物体と像のように一対の結像関係を満たしている点を意味しています。

【1-1】焦点距離と主点位置

光学系の焦点距離は、主点位置から焦点までの距離により定義されます。

このとき、対応する焦点が像側焦点か物体側焦点かによって、主点は像側主点と物体側主点の2つに分けられます。

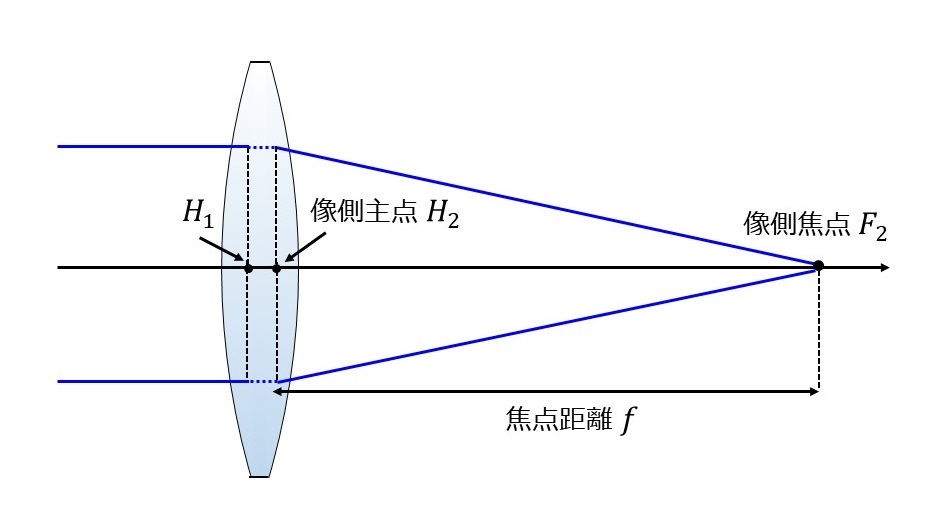
無限遠の物体から光学系に入射する光線は、像側焦点\(\hspace{2pt}\large{F_2}\hspace{2pt}\)に結像します。このとき、像側主点位置\(\hspace{2pt}\large{H_2}\hspace{2pt}\)から像側焦点\(\hspace{2pt}\large{F_2}\hspace{2pt}\)までの距離が焦点距離となります。

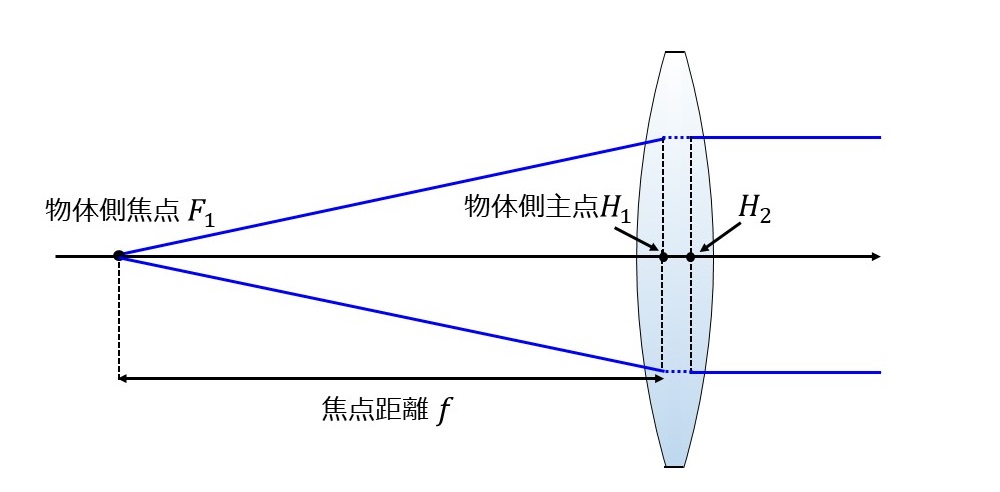
一方、像側から平行光線を入射させた場合、物体側焦点\(\hspace{2pt}\large{F_1}\hspace{2pt}\)に結像します。このとき、物体側主点位置\(\hspace{2pt}\large{H_1}\hspace{2pt}\)から像側焦点\(\hspace{2pt}\large{F_1}\hspace{2pt}\)までの距離が焦点距離となります。

【1-2】像側主点位置

像側主点の位置は、作図により求めることができます。

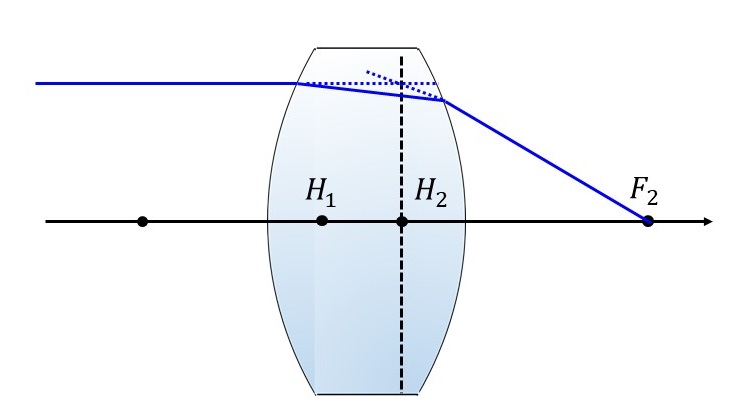
図3に、1枚の厚みのある正レンズの像側主点の位置を示します。
像側主点を作図するときは、物体側から平行に入射する光線を考えます。平行に入射した光線は、光学系の像側焦点\(\hspace{2pt}\large{F_2}\hspace{2pt}\)の位置に集光します。
このとき、物体側から平行に入射する光線を延長した線と、像側焦点\(\hspace{2pt}\large{F_2}\hspace{2pt}\)へ集光する光線を逆方向に延長した線の交点から、光軸に垂直に下した位置が像側主点の位置となります。

【1-3】物体側主点位置

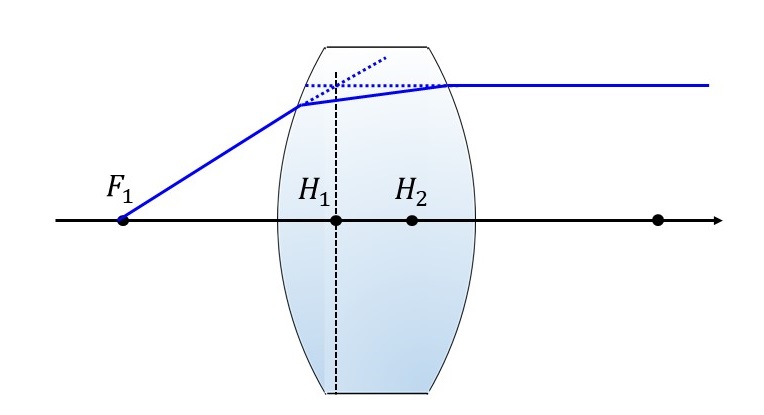
物体側主点の位置も図4のように作図で求めることができます。

像側から平行に入射する光線を考えると、光学系の像側焦点\(\hspace{2pt}\large{F_1}\hspace{2pt}\)の位置に集光します。
このとき、像側から平行に入射する光線を延長した線と、像側焦点\(\hspace{2pt}\large{F_1}\hspace{2pt}\)へ集光する光線を逆方向に延長した線の交点から、光軸に垂直に下した位置が物体側主点の位置となります。

【1-4】任意の光学系の主点位置

単レンズに限らず、複数のレンズを持った任意の光学系に対しても、同様の作図で主点位置を求めることができます。

図5に負レンズと正レンズの2枚で構成された光学系の像側主点位置を示します。

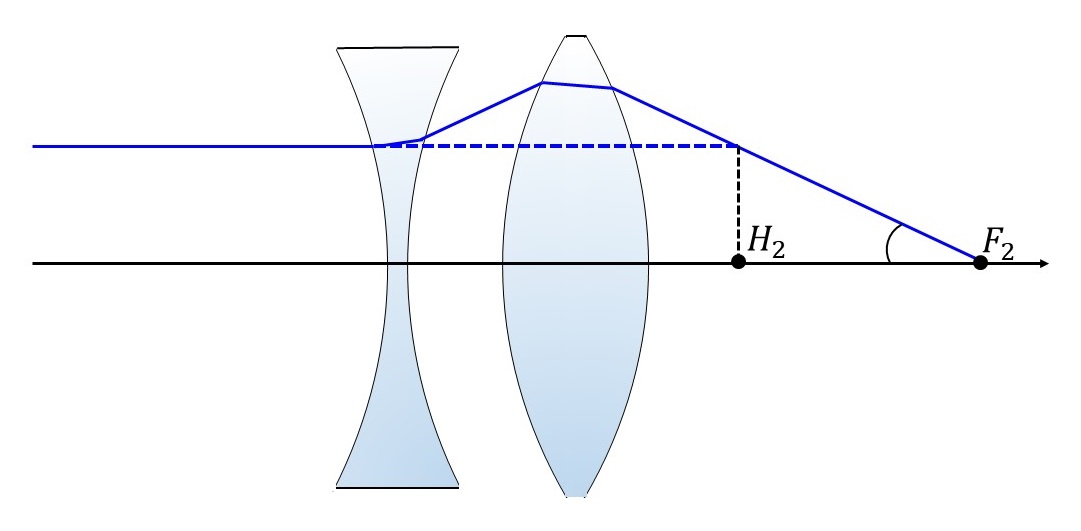
単レンズの場合と同様に、物体側から平行に入射する光線を延長した線と、像側焦点\(\hspace{2pt}\large{F_2}\hspace{2pt}\)に集光する光線の交点から、光軸に垂直に下した位置が組み合わせレンズの像側主点の位置になります。

【2】主点位置の計算

光学系の主点位置は、近軸光線追跡により計算することができます。

図6に、物体側から任意の光学系に平行光を入射させた様子を図示します。 図中では、光学系の最終面を基準にした像側主点の位置を\(\hspace{2pt}\large{\Delta_2}\hspace{2pt}\)、光学系の最終面から焦点までを\(\hspace{2pt}\large{s_k'}\hspace{2pt}\)、焦点距離を\(\hspace{2pt}\large{f}\hspace{2pt}\)としています。

光学系に高さ\(\hspace{2pt}\large{h_1}\hspace{2pt}\)で平行に入射した近軸光線を延長すると、像側主点位置\(\hspace{2pt}\large{H_2}\hspace{2pt}\)において高さ\(\hspace{2pt}\large{h_1}\hspace{2pt}\)となります。
また、最終レンズ面(第k面)における光線の高さ\(\hspace{2pt}\large{h_k}\hspace{2pt}\)は近軸光線追跡により計算されます。

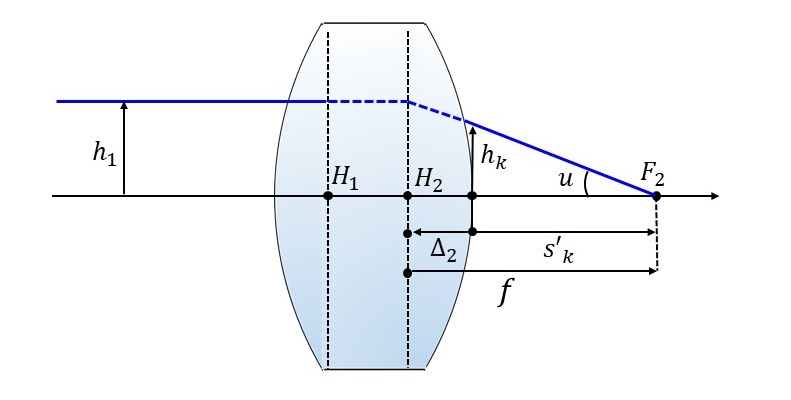
像側主点位置\(\hspace{2pt}\large{\Delta_2}\hspace{2pt}\)は、図6に示される幾何学的な関係から、近軸光線追跡の計算結果を利用して(1)式のように計算されます。

(1)式中の屈折率\(\large{\hspace{2pt}N\hspace{2pt}}\)は媒質の屈折率です。空気中の光学系では\(\hspace{2pt}\large{N=1}\hspace{2pt}\)と計算します。

物体側主点の位置を計算する場合は、像側から平行光を入射させて同様の計算を行います。

【2-1】計算例 : 両凸レンズの主点位置

計算例として、両凸レンズの主点位置を計算します。

計算する両凸レンズは第1面の曲率\(\hspace{2pt}\large{R\hspace{1pt}1=100\hspace{2pt}[mm]}\hspace{2pt}\),第2面の曲率\(\hspace{2pt}\large{R\hspace{1pt}2=-100\hspace{2pt}[mm]}\hspace{2pt}\), 厚さ\(\hspace{2pt}\large{d=5\hspace{2pt}[mm]}\hspace{2pt}\), 硝材の屈折率\(\hspace{2pt}\large{n=1.5}\hspace{2pt}\)とします。

両凸レンズに近軸計算を実施した結果は以下のようになります。

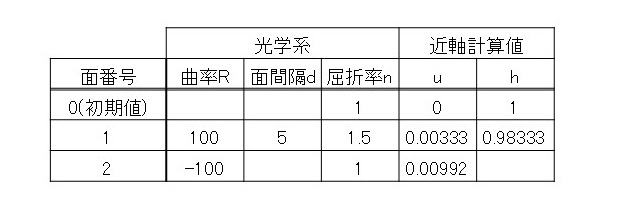
この計算結果から、像側主点位置\(\hspace{2pt}\large{\Delta_2}\hspace{2pt}\)は(1)式より、 \begin{eqnarray} \large \Delta_2&\large =&\large \frac{h_k-h_1}{Nu}\\[0.7em] &\large =&\large \frac{0.98333-1}{0.00992}\\[0.7em] &\large =&\large -1.68 \hspace{3pt}[mm] \end{eqnarray} と計算されます。

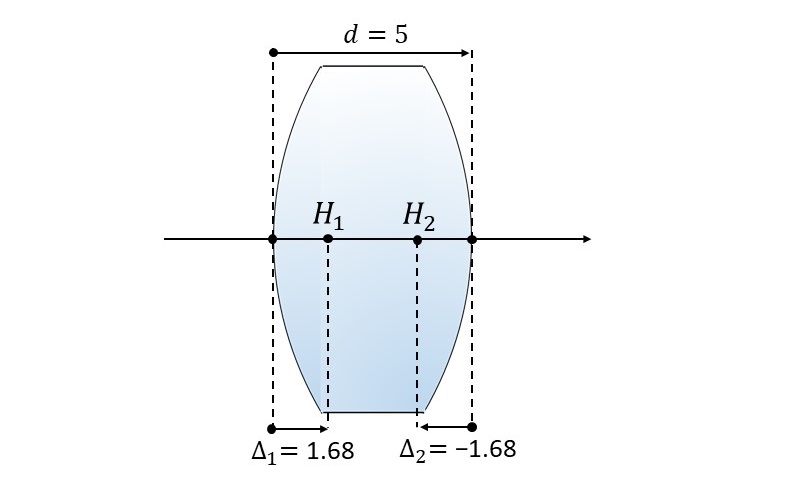
同様に物体側主点位置\(\hspace{2pt}\large{\Delta_1}\hspace{2pt}\)についても計算すると、\(\hspace{2pt}\large{\Delta_1 =1.68 \hspace{3pt}[mm]}\hspace{2pt}\)となります。

上記の計算結果を図示すると、主点位置は以下の図5のようになります。

上記の主点位置は、当サイトで公開している【計算ツール】単レンズの焦点距離,主点,体積で計算することができます。

【3】主点位置基準の結像

主点位置を基準とすることで、複数のレンズから構成される光学系の近軸結像関係を、1枚の薄肉レンズ(屈折面)の結像に見なすことができます。

図9に、物体側から負レンズ1枚、正レンズ1枚が並んだ光学系を、1枚の薄肉レンズに見なして描いた図を示します。

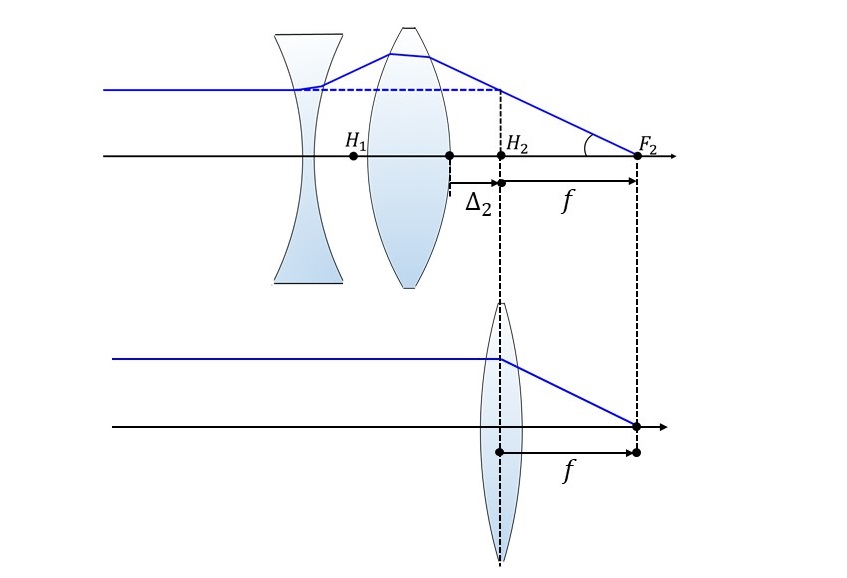
図中では、2枚のレンズから成る光学系の像側主点位置を\(\hspace{2pt}\large{H_2}\hspace{2pt}\)、合成焦点距離を\(\hspace{2pt}\large{f}\hspace{2pt}\)、光学系最終面から像側主点までの距離を\(\hspace{2pt}\large{\Delta_2}\hspace{2pt}\)としています。

このとき、像側主点の位置\(\hspace{2pt}\large{H_2}\hspace{2pt}\)に焦点距離\(\hspace{2pt}\large{f}\hspace{2pt}\)の薄肉レンズがあると考えると、2枚のレンズからなる光学系を1枚の薄肉レンズと見なすことができます。

このように複雑な光学系であっても、主点位置を基準とすることで1枚の薄肉レンズと等価な近軸関係を持つと見なすことができます。 この性質を利用すれば、光学系の焦点距離と主点位置を先に計算しておくことで、結像位置や倍率といった近軸計算を簡単に実行することができます。

参考文献

---