-光と光学に関連する用語の解説サイト-

近軸光線追跡

本項では、以下の内容について解説します。

・近軸光線追跡の近似とは何か
・近軸光線追跡の計算方法
・厚肉レンズや2枚の薄肉レンズの合成焦点距離など近軸計算の具体例

1. 近軸光線追跡とは
- 1-1. 近軸近似とは
2. 近軸光線追跡の計算式
3. 近軸光線追跡の計算方法
参考文献

【1】近軸光線追跡とは

近軸光線追跡とは、光軸に限りなく近傍した領域で、光線の屈折角や結像位置を計算する方法のことです。

通常の光線追跡は、スネルの法則を厳密に計算するため、屈折面で発生する収差の影響を含んでいます。
一方、近軸光線追跡は、光軸に限りなく近い領域で屈折が発生すると近似することで、収差の影響を含めずに光線の角度や高さを計算することができます。(ただし、近軸領域であっても屈折率の波長分散が存在するため、色収差は発生します。)

そのため、近軸光線追跡は、光学系の理想的な焦点距離や結像位置を求めるために使用されています。

【1-1】近軸近似とは

通常の光線追跡では、入射角度を$\hspace{2pt}\large{\theta}\hspace{2pt}$、屈折率を$\hspace{2pt}\large{n}\hspace{2pt}$としたとき、面の屈折をスネルの法則により計算を行います。 $$\large{n_1\sin\theta_1=n_2\sin\theta_2}$$

一方、近軸光線追跡では入射角度$\hspace{2pt}\large{\theta}\hspace{2pt}$が十分小さいと近似して計算を行います。このような近似を近軸近似といいます。
$\hspace{2pt}\large{\sin\theta}\hspace{2pt}$をテイラー展開により表現すると、以下のようになります。 $$\large{\sin\theta=\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots}$$

ここで、入射角度$\hspace{2pt}\large{\theta}\hspace{2pt}$が十分に小さいとき、上式より$\hspace{2pt}\large{\sin\theta}\hspace{2pt}$は以下のように近似できます。 $$\large{\sin\theta\fallingdotseq\theta}$$

近軸光線追跡では、角度$\hspace{2pt}\large{\theta}\hspace{2pt}$が十分に小さいとして、スネルの法則を(1)式のように変形して光線追跡を行います。

【近軸近似のスネルの法則】

$\hspace{2pt}\large{\displaystyle n_1 \hspace{1pt} \theta_1=n_2 \hspace{1pt} \theta_2\hspace{20pt}(1)}\hspace{2pt}$

(1)式により光線追跡を計算することで、近軸領域の結像関係を計算することができます。

近軸近似として$\hspace{2pt}\large{\large{\sin\theta\fallingdotseq\theta}}\hspace{2pt}$以外にも、以下の近似式が使用されます。 $$\large{\large{\tan\theta\fallingdotseq\theta}}$$ $$\large{\large{\cos\theta\fallingdotseq 1}}$$

【2】近軸光線追跡の計算式

近軸光線追跡は、第$\hspace{2pt}\large{i}\hspace{2pt}$面における屈折と、第$\hspace{2pt}\large{i}\hspace{2pt}$面から第$\hspace{2pt}\large{i+1}\hspace{2pt}$面間の転送を交互に計算することで、光学系全体の光線の角度や結像位置の計算を行います。
そのため、計算式には屈折式と転送式の2種類があります。

また、近軸光線追跡には、結像位置$\hspace{2pt}\large{s}\hspace{2pt}$の1変数を使用する場合と、光線角度$\hspace{2pt}\large{u}\hspace{2pt}$と光線高さ$\hspace{2pt}\large{h}\hspace{2pt}$の2変数を使用する場合があります。

【2-1】近軸光線追跡の計算式(1変数)

以下に近軸光線追跡を結像位置$\hspace{2pt}\large{s}\hspace{2pt}$の1変数で計算する場合を示します。

【近軸追跡の一般式(1変数)】

(屈折式) $\hspace{2pt}\large{\displaystyle \hspace{10pt}\frac{N'_i}{s'_i}=\frac{N_i}{s_i}+\frac{N'_i-N_i}{r_i}}\hspace{2pt}$
(転送式) $\hspace{2pt}\large{\displaystyle \hspace{28pt}s_{i+1}=s'_i-d'_i\hspace{19pt}}\hspace{2pt}$

$\hspace{2pt}\large{N}\hspace{2pt}$は屈折率、$\hspace{2pt}\large{s}\hspace{2pt}$は屈折面からの距離、$\hspace{2pt}\large{r}\hspace{2pt}$は曲率半径、$\hspace{2pt}\large{d}\hspace{2pt}$は屈折面の間隔を表します。

また、iは第i番目の屈折面の計算であることを表します。第i面を屈折面としたとき、$\hspace{2pt}\large{N}\hspace{2pt}$は屈折前、$\hspace{2pt}\large{N'}\hspace{2pt}$は屈折後の屈折率を表します。

【2-2】近軸光線追跡の計算式(2変数)

以下に近軸光線追跡を光線角度$\hspace{2pt}\large{u}\hspace{2pt}$と光線高さ$\hspace{2pt}\large{h}\hspace{2pt}$の2変数で計算する場合を示します。

【近軸追跡の一般式(2変数)】

(屈折式)$\hspace{2pt}\large{\displaystyle \hspace{10pt}N'_iu'_i=N_iu_i+h_i\frac{N'_i-N_i}{r_i}}\hspace{2pt}$
(転送式) $\hspace{2pt}\large{\displaystyle \hspace{20pt}u_{i+1}=u'_i\hspace{65pt}}\hspace{2pt}$
$\hspace{2pt}\large{\displaystyle \hspace{24pt}h_{i+1}=h_i-d'_iu'_i}\hspace{2pt}$

$\hspace{2pt}\large{N}\hspace{2pt}$は屈折率、$\hspace{2pt}\large{u}\hspace{2pt}$は光線の光軸からの角度、$\hspace{2pt}\large{h}\hspace{2pt}$は光軸からの高さ、$\hspace{2pt}\large{r}\hspace{2pt}$は曲率半径を表します。

補足【2種類の計算式の使い分け】

近軸計算には『結像位置$\hspace{2pt}\large{s}\hspace{2pt}$の1変数を使用する方法』と『角度$\hspace{2pt}\large{u}\hspace{2pt}$,光線の高さ$\hspace{2pt}\large{h}\hspace{2pt}$の2変数を使用する方法』の2通りの計算方法があります。

1変数の場合は結像位置$\hspace{2pt}\large{s}\hspace{2pt}$が計算結果として出てくるので、結像位置の情報が必要な場合に使用されます。
(例えば、単レンズの結像位置を計算する公式を簡単に求めることができます。)

ただし、計算の媒介変数である結像位置$\hspace{2pt}\large{s}\hspace{2pt}$が分数の分母に入っているため、複数のレンズから構成される光学系の場合、計算が非常に複雑になってしまいます。

一方、2変数$\hspace{2pt}\large{u,h}\hspace{2pt}$の近軸光線追跡は、計算を線形の積で実行できるというメリットがあります。この性質を利用して、後述する行列計算によって簡単に計算をすることができます。

複数のレンズを使用した光学系では、この計算上のメリットから2変数$\hspace{2pt}\large{u,h}\hspace{2pt}$により近軸光線追跡を行うことが多いです。

【2-3】近軸光線追跡の行列計算

2変数を使用した近軸光線追跡は以下のように行列によって計算することができます。

【近軸光線追跡の行列式】

(屈折式) $\hspace{13pt}\large{\displaystyle \begin{pmatrix} h_i \\ N'_iu'_i \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ \frac{N'_i-N_i}{r_i} & 1 \end{pmatrix} \begin{pmatrix} h_i \\ N_iu_i \end{pmatrix}}$
(転送式) $\large{\displaystyle \begin{pmatrix} h_{i+1} \\ N_{i+1}u_{i+1} \end{pmatrix} = \begin{pmatrix} 1 & -\frac{d'_i}{N'_i} \\ 0 & 1 \end{pmatrix} \begin{pmatrix} h_i \\ N'_iu'_i \end{pmatrix}}$

したがって、第1面から第i面までの近軸光線は以下のような行列によって計算することができます。

【第i面までの近軸光線追跡の行列計算】

$$\large \displaystyle \hspace{10pt} \begin{pmatrix} h_i \\ N'_iu'_i \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ \frac{N'_i-N_i}{r_i} & 1 \end{pmatrix} \begin{pmatrix} 1 & -\frac{d\hspace{1pt}'_{i-1}}{N'_{i-1}} \\ 0 & 1 \end{pmatrix} \cdots \begin{pmatrix} 1 & 0 \\ \frac{N'_1-N_1}{r_1} & 1 \end{pmatrix} \begin{pmatrix} h_1 \\ N_1u_1 \end{pmatrix}\hspace{10pt}$$

【3】近軸光線追跡の計算方法

本章では、厚肉レンズや複数の薄肉レンズからなる光学系の近軸光線追跡の計算方法について解説します。

【3-1】近軸光線追跡の焦点距離の計算

近軸光線追跡の例として、厚みのある単レンズの焦点距離を求めます。
第1面、第2面の曲率半径がそれぞれ$\hspace{2pt}\large{r_1,r_2}\hspace{2pt}$、レンズの厚みが$\hspace{2pt}\large{d}\hspace{2pt}$、屈折率が$\hspace{2pt}\large{N}\hspace{2pt}$とします。厚肉レンズの焦点距離

図1.厚肉レンズの焦点距離

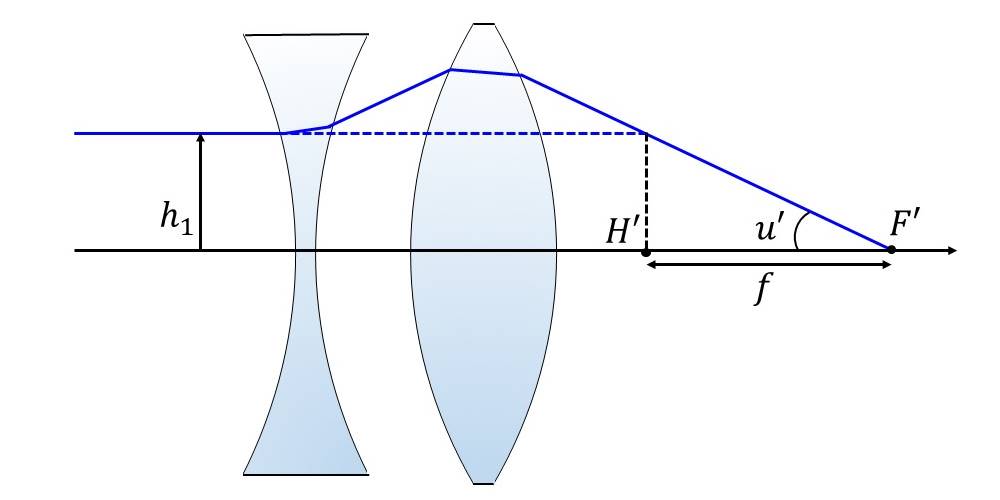
上図にも示されているように、光学系の焦点距離は主点位置$\hspace{2pt}\large{H}\hspace{2pt}$から焦点$\hspace{2pt}\large{F}\hspace{2pt}$までの距離で定義されます。

図1より主点$\hspace{2pt}\large{H}\hspace{2pt}$の位置は、"光軸に平行に入射する光線"と"最終面から焦点へ入射する光線"をそれぞれ延長した線の交わる位置から、光軸に垂線を下した位置となります。

入射光の高さを$\hspace{2pt}\large{h_1}\hspace{2pt}$、最終面から焦点への角度を$\hspace{2pt}\large{u_2'}\hspace{2pt}$とすると、近軸近似における焦点距離$\hspace{2pt}\large{f}\hspace{2pt}$は以下の式により求められます。 $$\large{f=\frac{h_1}{u_2'}}$$

(なお上式には、近軸近似である$\hspace{2pt}\large{\tan u \fallingdotseq u}\hspace{2pt}$が使用されています。)

【3-2】厚肉レンズの焦点距離の計算

実際に、図1の厚肉レンズの焦点距離を計算します。

まず、実際に【2-3】近軸光線追跡の行列計算に、厚肉レンズのパラメータを代入します。

$$\hspace{10pt}\displaystyle \large \begin{pmatrix} h_2 \\ u'_2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ \frac{1-N}{r_2} & 1 \end{pmatrix} \begin{pmatrix} 1 & -\frac{d}{N} \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ \frac{N-1}{r_1} & 1 \end{pmatrix} \begin{pmatrix} h_1 \\ u_1 \end{pmatrix}\hspace{10pt}$$

ここで、焦点距離を求める場合、平行光を入射するため入射光の光線角度は$\hspace{2pt}\large{u_1=0}\hspace{2pt}$とします。
また、入射光の高さ$\hspace{2pt}\large{h_1}\hspace{2pt}$は計算しやすいように$\hspace{2pt}\large{h_1=1}\hspace{2pt}$とします。($\hspace{2pt}\large{h_1}\hspace{2pt}$はゼロ以外の数であれば、どの値でも同様の結果となります。)

上式を計算すると、以下のようになります。

$$\hspace{10pt}\displaystyle \large \begin{pmatrix} h_2 \\ u'_2 \end{pmatrix} = \begin{pmatrix} 1-\frac{d}{N} \frac{N-1}{r_1} & -\frac{d}{N} \\ (N-1)(\frac{1}{r_1}-\frac{1}{r_2}) +\left(\frac{d}{N}\right)\frac{(N-1)^2}{r_1r_2} & 1-\frac{d}{N} \frac{1-N}{r_2} \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}\hspace{10pt}$$

したがって、焦点距離$\hspace{2pt}\large{f}\hspace{2pt}$は以下のように求められます。

$$\hspace{10pt}\large \frac{1}{f}=\frac{u_2'}{h_1}=(N-1)(\frac{1}{r_1}-\frac{1}{r_2}) +\left(\frac{d}{N}\right)\frac{(N-1)^2}{r_1r_2}\hspace{10pt}$$

【3-3】光線行列(ABCD行列)

光学系全体の近軸光線追跡を計算する行列を、光線行列(もしくはABCD行列)という言い方をします。
上記した近軸近似の焦点距離では、$\hspace{2pt}\large{2 \times 2}\hspace{2pt}$の行列が光線行列(ABCD行列)に相当します。

ここで、光学系全体の近軸光線追跡が以下のように表されるとします。 $$\displaystyle \large \begin{pmatrix} h_i \\ u'_i \end{pmatrix} = \begin{pmatrix} A & B \\ C & D \end{pmatrix} \begin{pmatrix} h_1 \\ u_1 \end{pmatrix}$$ このとき、焦点距離$\hspace{2pt}\large{f}\hspace{2pt}$は行列の成分$\hspace{2pt}\large{C}\hspace{2pt}$と、$\hspace{2pt}\displaystyle\large{\frac{1}{f}=C}\hspace{2pt}$の関係にあります。

【3-4】複数の薄肉レンズの焦点距離の計算

次に、図2のような複数の薄肉レンズの合成焦点距離の計算について示します。 2枚の薄肉レンズの焦点距離

図2.2枚の薄肉レンズの焦点距離

先述した厚肉レンズの焦点距離の計算結果から、厚みの無視できる焦点距離$\hspace{2pt}\large{f}\hspace{2pt}$の薄肉レンズ($\hspace{2pt}\large{d=0}\hspace{2pt}$)の行列計算の式は以下のようなります。 $$\large \begin{pmatrix} 1& 0 \\ \frac{1}{f} & 1 \end{pmatrix}$$

この行列式を屈折式とすることで、間隔$\hspace{2pt}\large{d}\hspace{2pt}$の焦点距離$\hspace{2pt}\large{f_1,f_2}\hspace{2pt}$の2枚の薄肉レンズの焦点距離を計算します。

$$\hspace{10pt}\displaystyle \large \begin{pmatrix} h_2 \\ u'_2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ \frac{1}{f_2} & 1 \end{pmatrix} \begin{pmatrix} 1 & -d \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ \frac{1}{f_1} & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}\hspace{10pt}$$

上式を計算すると、以下のようになります。

$$\hspace{10pt}\displaystyle \large \begin{pmatrix} h_2 \\ u'_2 \end{pmatrix} = \begin{pmatrix} 1- \frac{d}{f_1} & -d \\ \frac{1}{f_1} + \frac{1}{f_2}- \frac{d}{f_1 f_2} & 1-\frac{d}{f_2} \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}\hspace{10pt}$$

したがって、焦点距離$\hspace{2pt}\large{f}\hspace{2pt}$は以下のように求められます。 $$\large \frac{1}{f}=\frac{u_2'}{h_1} =\frac{1}{f_1} + \frac{1}{f_2}- \frac{d}{f_1 f_2} $$

別のページに本章の近軸光線追跡を使用した組み合わせレンズの計算ツールを作成しています。