開口数とは
本項では、以下の内容について解説します。
- ・開口数の定義
- ・空間分解能との関係
- ・焦点深度との関係
- ・像の明るさとの関係
【1】開口数NAとは
開口数(numerical aperture)とは、レンズが光をどれだけ効率良く集光するかを示す指標です。
開口数が大きいほど、そのレンズによって作られる像は明るくなります。
開口数がレンズの性能を代表する値の1つとして使用される理由は、『異なる構成のレンズであっても、開口数を比較することで像の明るさを簡単に比較することができる』という点にあります。
また、開口数が大きいほど、そのレンズの空間分解能は高く、焦点深度は小さくなる性質があります。そのため、開口数は空間分解能や焦点深度の目安としても使用されます。
【1-1】開口数の定義式
図1のような顕微鏡の対物レンズについて考えます。
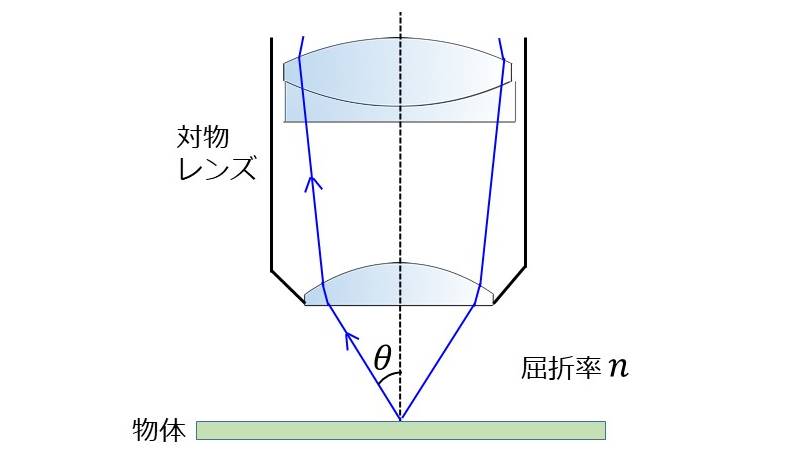
物体からレンズに入射する光のうち、光軸となす角度が最大の角度を\(\hspace{2pt}\large{\theta}\hspace{2pt}\)、物体とレンズの間の媒質の屈折率を\(\hspace{2pt}\large{n}\hspace{2pt}\)とすると、開口数は以下の式により定義されます。
(1)式の屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)は、物体とレンズの間の屈折率であり、通常は空気のため\(\hspace{2pt}\large{n=1}\hspace{2pt}\)となります。
したがって、空気中では開口数\(\hspace{2pt}\large{NA}\hspace{2pt}\)は1より小さい値を取ることになります。
【2】開口数と空間分解能の関係式
開口数は、空間分解能(resolution)の指標として使用されます。
空間分解能とは、観測された像から判別できる2点の物体間の最短距離によって定義されます。
開口数を\(\hspace{2pt}\large{NA}\hspace{2pt}\)、使用する波長を\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)とすると、空間分解能\(\hspace{2pt}\large{R}\hspace{2pt}\)は以下のように表されます。
(2)式より、空間分解能を向上させる(\(\hspace{2pt}\large{R}\hspace{2pt}\)を小さくする)ためには以下の方法が取られます。
- 使用する波長\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)をより短波長にする
- 開口数\(\hspace{2pt}NA\hspace{2pt}\)がより大きいレンズを使用する
- 物体とレンズ間の媒質の屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)を大きくする
『1.使用する波長\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)をより短波長にする』に関しては、人の眼での観察を前提とすると、可視光域が380nm(紫色)~780nm(赤色)であるため、最も短波長の380nmが限度となります。
『3.物体とレンズ間の媒質の屈折率\(\hspace{2pt}\large{n}\hspace{2pt}\)を大きくする』方法として、物体とレンズの間に屈折率の高い液体を入れることで開口数\(\hspace{2pt}\large{NA}\hspace{2pt}\)を大きくすることができます。このような方法を液浸といいます。
なお、(2)式で計算される空間分解能は、光の回折の影響のみを考慮した分解能です。(2)式ではレンズで発生する収差を考慮していないため、実際には収差にも影響されて空間分解能は悪化します。
【3】開口数と焦点深度の関係式
開口数は、焦点深度(depth of focus)とも関係があります。
焦点深度とは、物体の前後方向にピントが合う範囲のことをいいます。
開口数を\(\hspace{2pt}\large{NA}\hspace{2pt}\)、使用する波長を\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)とすると、焦点深度\(\hspace{2pt}\large{\delta}\hspace{2pt}\)は以下のように表されます。
(3)式より、開口数\(\hspace{2pt}\large{NA}\hspace{2pt}\)が大きく、また使用する波長が短いほど、焦点深度が小さくなることが分かります。
顕微鏡の場合は、対物レンズの開口数\(\hspace{2pt}\large{NA}\hspace{2pt}\)が大きいほど、物体の前後方向に対してピントの合う範囲が小さくなります。
【4】開口数と像の明るさの関係式
像の明るさ (照度\(\hspace{2pt}\large{E}\hspace{2pt}\) = 単位面積あたりの光エネルギー) は、使用するレンズの開口数\(\hspace{2pt}\large{NA}\hspace{2pt}\) と 横倍率\(\hspace{2pt}\large{\beta}\hspace{2pt}\) によって以下の式で表されます。
(4)式より、開口数の大きいレンズを使用すると、その2乗に比例して像が明るくなることが分かります。
また、像の明るさはレンズの倍率\(\hspace{2pt}\large{\beta}\hspace{2pt}\)にも依存します。
倍率\(\hspace{2pt}\large{\beta}\hspace{2pt}\)が大きい(高倍率)ほど、像は拡大されて単位面積あたりの光エネルギーが小さくなることで、像は暗くなります。
顕微鏡の対物レンズを変更すると、光学系の開口数NAと倍率\(\hspace{2pt}\large{\beta}\hspace{2pt}\)が変化することで、(4)式にしたがって像の明るさが変化します。
開口数には、物体側で定義される物体側開口数と、像側で定義される像側開口数の2種類があります。
光学顕微鏡では、対物レンズの物体側開口数によって像の明るさが変わるため、開口数というと物体側開口数のことを指します。
図2のように、光軸上の物体から放出される光のうち、入射瞳に向かって最大の角度となる光線の角度を\(\hspace{2pt}\large{\theta}\hspace{2pt}\)とします。また、射出瞳から像点に向かう光のうち、最大の光線の角度を\(\hspace{2pt}\large{\theta\hspace{1pt}'}\hspace{2pt}\)とします。
また、物体側の屈折率を\(\hspace{2pt}\large{n}\hspace{2pt}\)、像側の屈折率を\(\hspace{2pt}\large{n'}\hspace{2pt}\)とします。
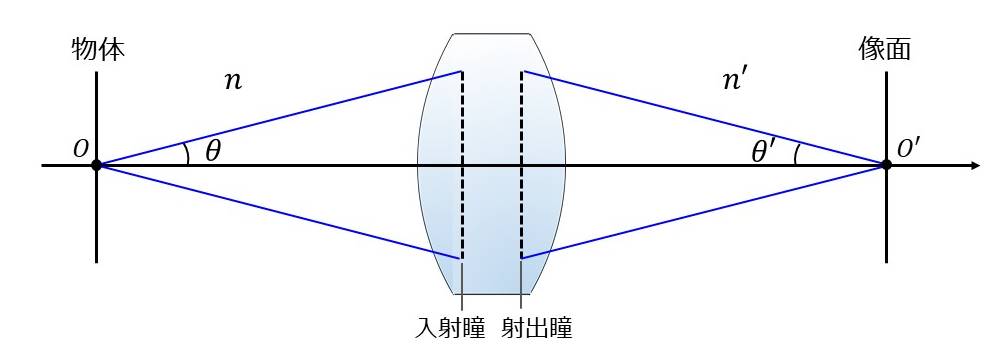
このとき、物体側開口数\(\hspace{2pt}\large{NA}\hspace{2pt}\)は、これまで説明したように以下のように定義されます。 $$\large{ NA = n \sin \theta}$$ また、像の明るさ\(\hspace{2pt}\large{E}\hspace{2pt}\)は以下のように表されます。 $$\large{ \displaystyle E\propto\frac{(NA)^{\hspace{1pt}2}}{\beta^{\hspace{1pt}2}} = \frac{(n \sin u)^{\hspace{1pt}2}}{\beta^{\hspace{1pt}2}}}$$
一方、像側開口数\(\hspace{2pt}\large{NA'}\hspace{2pt}\)は、以下のように定義されます。 $$\large{ NA' = n' \sin \theta\hspace{1pt}'}$$ また、像の明るさ\(\hspace{2pt}\large{E}\hspace{2pt}\)は以下のように表されます。 $$\large{ \displaystyle E\propto(NA')^{\hspace{1pt}2} = (n' \sin u')^{\hspace{1pt}2}}$$
物体側開口数と像側開口数では、像の明るさを表現するときに倍率\(\hspace{2pt}\large{\beta}\hspace{2pt}\)が関係するかどうかが異なります。
【補足】開口数と像の明るさの関係式の導出
像の明るさとは、像面における照度E (単位面積あたりの光エネルギー) から計算されます。
本章では、像の明るさ(照度E)を開口数 \(\hspace{2pt}\large{NA = n \sin \theta}\hspace{2pt}\) で表現する式を導きます。
開口数と像の明るさの関係を導く過程は少々複雑ですが、導出過程を知ることで『開口数NAとは、そもそも何を表しているのか』を理解するのに役立つと思います。
・光源から放出されるエネルギー(光束)の計算
像面における照度を求める準備として、光源から放出され、光学系に入射する光のエネルギー(光束)を計算します。
図3のように、点\(\large\hspace{1pt}O\hspace{1pt}\)に輝度\(\large\hspace{1pt}B\hspace{1pt}\)の光を放出する面積\(\large\hspace{1pt}dS\hspace{1pt}\)の光源があるとします。(輝度\(\large\hspace{1pt}B\hspace{1pt}\)は見かけの単位面積、単位立体角あたりに放出される光のエネルギーを表します。)
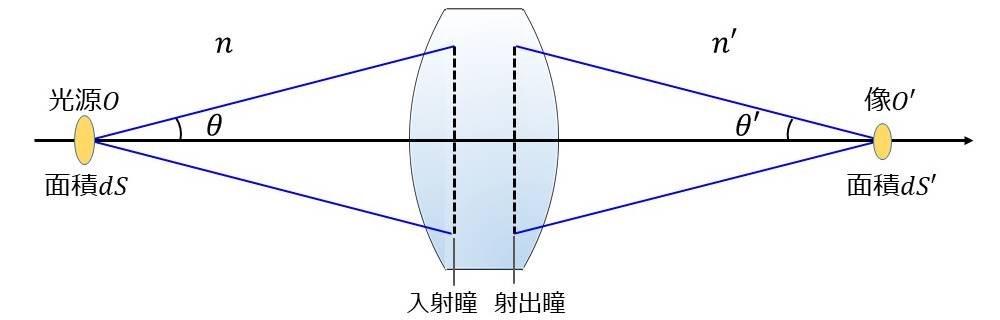
光源の輝度\(\large\hspace{2pt}B\hspace{2pt}\)を光度\(\large\hspace{2pt}I\hspace{2pt}\)により表現すると、以下の式となります。(輝度\(\large\hspace{1pt}I\hspace{1pt}\)は、単位立体角あたりに放出される光のエネルギーを表します。)
ここで、光源から放出されるエネルギーのうち、光学系の入射瞳に張る半角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)内の光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)を計算します。
光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)は、光度\(\large\hspace{2pt}I\hspace{2pt}\)を半角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)で表される立体角で積分することで得られます。 $$\large{\phi=\int_0^{\theta} I d\Omega}$$
ここで、\(\hspace{2pt}\large{I=B \, dS \cos \theta}\hspace{2pt}\)、\(\hspace{2pt}\large{d \Omega = 2\pi\sin \theta \, d\theta}\hspace{2pt}\)より、光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)は以下のように計算されます。
(5)式が光源から放射される光のエネルギーを半角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)で表現した式となります。
・像面に集光する光のエネルギー(光束)の計算
一方、面積\(\large\hspace{2pt}dS\hspace{2pt}\)、輝度\(\large\hspace{2pt}B\hspace{2pt}\)の光源から放出された光が、面積\(\large\hspace{2pt}dS'\hspace{2pt}\)、輝度\(\large\hspace{2pt}B'\hspace{2pt}\)の像として集光したとすると、(5)式と同様の計算により、像面の\(\large\hspace{2pt}dS'\hspace{2pt}\)に集光する光束\(\hspace{2pt}\large{\phi'}\hspace{2pt}\)は以下となります。
ここで、光学系を光が通過するときに発生する反射や吸収によるエネルギーの損失を透過率\(\large\hspace{2pt}t\hspace{2pt}\)により表すと、入射光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)と射出光束\(\hspace{2pt}\large{\phi'}\hspace{2pt}\)の間には以下が成り立ちます。 $$\large{\phi'=t \hspace{1pt} \phi}$$
・光学系の明るさと開口数NAの関係
光学系の明るさは、像面の明るさを表す照度\(\displaystyle\hspace{2pt}\large{E=\frac{\phi'}{dS'}}\hspace{2pt}\)により計算されます。先述の像側に集光する光のエネルギー\(\hspace{2pt}\large{\phi'}\hspace{2pt}\)を代入して計算すると、 \begin{eqnarray} \displaystyle \large E& \large =&\large \frac{\phi'}{dS'}\\[0.5em] \displaystyle &\large =&\large t\frac{\phi}{dS'}\\[0.5em] \displaystyle &\large =&\large t \frac{\pi B dS\, {\sin}^2 \theta}{dS'}\\ \end{eqnarray}
ここで、\(\hspace{2pt}\large{dS}\hspace{2pt}\)と\(\hspace{2pt}\large{dS'}\hspace{2pt}\)を像倍率\(\hspace{2pt}\large{\beta}\hspace{2pt}\)で表すと、\(\displaystyle\hspace{2pt}\large{\beta^{\hspace{1pt}2}=\frac{dS'}{dS}}\hspace{2pt}\)の関係があるため、以下が成り立ちます。 $$\displaystyle \large{E=t \frac{\pi B \, {\sin}^{\hspace{1pt}2} \theta}{\beta^{\hspace{2pt}2}}\hspace{20pt}(6)}$$
ここで、(6)式を像面側の半角\(\hspace{2pt}\large{\theta\hspace{1pt}'}\hspace{2pt}\)により表現するため、アッベの正弦条件という関係式を使用します。
球面収差とコマ収差が除去された光学系では、以下のアッベの正弦条件が成り立ちます。 $$\large{\frac{n \sin \theta}{n' \sin \theta\hspace{1pt}'}=\beta}$$
アッベの正弦条件により、物体側の半角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)を像側の半角\(\hspace{2pt}\large{\theta\hspace{1pt}'}\hspace{2pt}\)により表現することができます。
$$\large{E=\frac{t \pi B}{n^2} {(n' \sin \theta\hspace{1pt}')}^2 \hspace{20pt}(7)}$$(7)式は、像面の明るさを像側開口数\(\large{\hspace{2pt}NA\hspace{2pt}}\)( \(\hspace{2pt}\large{n' \sin \theta\hspace{1pt}'}\hspace{2pt}\) )により表現する式です。
ここで、屈折率\(\large\hspace{2pt}n\hspace{2pt}\),輝度\(\large\hspace{2pt}B\hspace{2pt}\)は物体側のパラメータであり、透過率\(\large{\hspace{2pt}t\hspace{2pt}}\)はガラスの反射や吸収などが要因のため幾何学的な集光状態とは別問題であるとすると、 像面の明るさ\(\hspace{2pt}\large{E}\hspace{2pt}\)は\(\hspace{2pt}\large{n' \sin \theta\hspace{1pt}'}\hspace{2pt}\)の2乗に比例すると書き表せます。
また、(7)式を物体側開口数\(\large{\hspace{2pt}NA\hspace{2pt}}\)( \(\hspace{2pt}\large{n \sin \theta}\hspace{2pt}\) )による表記に書き換えた場合、以下の式となります。 $$\large{E=\frac{t \pi B}{n^2} \frac{{(n \sin \theta)}^2}{\beta^{\hspace{2pt}2}}}$$
上式から、光学系の明るさと物体側開口数の関係を表す式を得ることができます。
以上の導出過程から、開口数\(\hspace{2pt}\large{NA = n \sin \theta}\hspace{2pt}\) は、レンズ内で発生する反射や吸収、収差などの影響を無視し、幾何学的にどれだけ光を効率よく取り込み、集光するかを表す値だと分かります。
つまり、開口数は レンズの幾何学的な集光能力のみを数値化することで、異なるレンズ構成であっても、像の明るさを簡単に比較することを可能にしています。
参考文献
・(1)岸川利郎『ユーザーエンジニアのための光学入門』(株)オプトロニクス社,平成16年12月18年 第1版9刷発行, 第3章 絞りとレンズ系の明るさ(pp51~64)
・(2)鶴田匡夫『光の鉛筆』株式会社新技術コミュニケーションズ,1986年1月15日 第4刷発行,2.光学像の明るさ pp6~11