立体角とは

本項では、以下の内容について解説します。

• ・立体角の定義
• ・円錐の頂点の角度と立体角の変換
• ・立体角の計算例

【1】立体角の求め方

立体角とは、球面上のある部分の面積に対し、球の中心からどの程度の広がりを持つかを表現する量です。

立体角\(\hspace{2pt}\large{\Omega}\hspace{2pt}\)は、図1のような中心\(\hspace{2pt}\large{C}\hspace{2pt}\)、半径\(\hspace{2pt}\large{r}\hspace{2pt}\)の球面上において、ある部分の面積を\(\hspace{2pt}\large{S}\hspace{2pt}\)としたとき、以下の式により求められます。

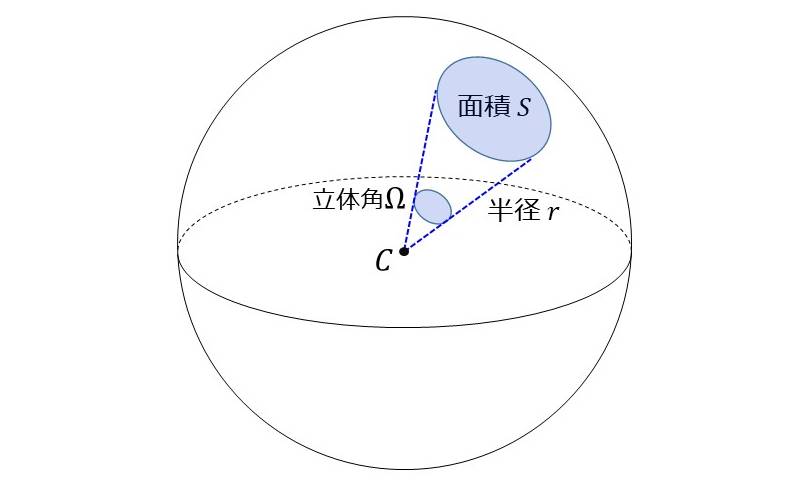
立体角の単位には[sr] (ステラジアン/steradian)を使用します。

測光の分野では、立体角は光源から放射される光束の広がり角、もしくは受光面への集光角を表す量として使用されます。

例えば、光度は「点光源から放出される単位立体角あたり光の明るさ」を意味します。
光度はカンデラ[cd] という単位を使用し、1ステラジアン[sr] あたりに1ルーメン[lm] の光束があるときに1カンデラ[cd] となります。

【2】円錐の頂点の角度と立体角の変換

光学の分野では、図2のような円錐の頂点の角度を、立体角に変換して計算することがあります。
本章では『円錐の頂点の角度\(\hspace{2pt}\large{u}\hspace{2pt}\)』と『立体角\(\hspace{2pt}\large{\Omega}\hspace{2pt}\)』の変換式を導きます。

図2のような球面上のある面積に対する円錐の頂点の角度が\(\hspace{2pt}\large{u}\hspace{2pt}\)であるときの立体角\(\hspace{2pt}\large{\Omega}\hspace{2pt}\)を求めます。(角度\(\hspace{2pt}\large{u}\hspace{2pt}\)は円錐の頂点の半頂角を表します。)

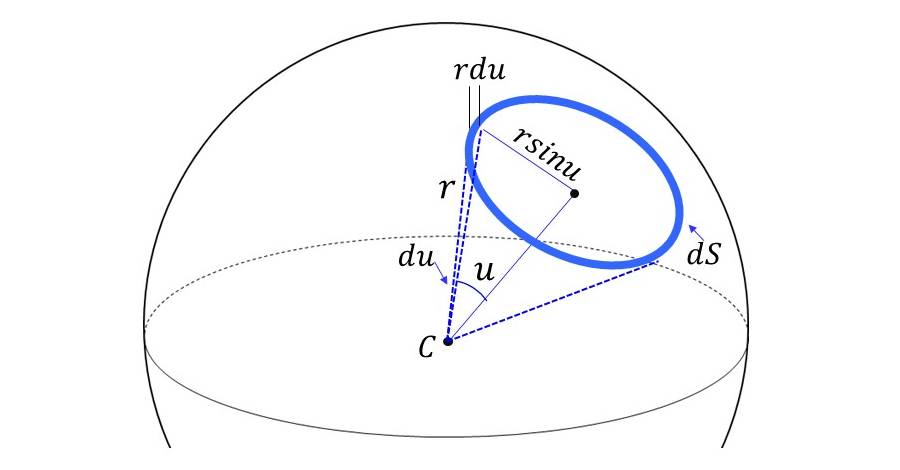
まず、微小な角度\(\hspace{2pt}\large{du}\hspace{2pt}\)によって計算される球面上の円環の面積\(\hspace{2pt}\large{ds}\hspace{2pt}\)を求めます。

円環の幅は、\(\hspace{2pt}\large{du}\hspace{2pt}\)と半径\(\hspace{2pt}\large{r}\hspace{2pt}\)から\(\hspace{2pt}\large{r・du}\hspace{2pt}\)となります。
また、図2より円環の半径が\(\hspace{2pt}\large{r・\sin u}\hspace{2pt}\)であるため、円環の円周は\(\hspace{2pt}\large{2\pi \hspace{1pt} r\sin u}\hspace{2pt}\)となります。以上から、円環の面積\(\hspace{2pt}\large{ds}\hspace{2pt}\)は(2)式のようになります。 $$\large{ds=2\pi \hspace{1pt}r\sin u・r \hspace{1pt} du\hspace{20pt}(2)}$$

(2)式の円環の面積を角度\(\hspace{2pt}\large{u}\hspace{2pt}\)で積分することで、頂点の角度\(\hspace{2pt}\large{u}\hspace{2pt}\)の円錐の球面上の面積\(\hspace{2pt}\large{S}\hspace{2pt}\)を求めます。 \begin{eqnarray} \large S& \large =&\large \int_0^u 2\pi\hspace{1pt} r\sin u・rdu \\[0.7em] \large &\large =&\large 2\pi \hspace{1pt} r^2 \int_0^u \sin udu \\[0.7em] \large &\large =&\large 2\pi \hspace{1pt} r^2 (1-\cos u) \end{eqnarray}

円錐の球面上の面積\(\hspace{2pt}\large{S}\hspace{2pt}\)を立体角の定義式(1)に代入し、立体角\(\hspace{2pt}\large{\Omega}\hspace{2pt}\)を計算すると以下のようなります。 \begin{eqnarray} \large \Omega&\large =&\large \frac{S}{r^2}\\[0.7em] \large &\large =&\large \frac{2\pi r^2 (1-\cos u)}{r^2}\\[0.7em] \large &\large =&\large 2\pi (1-\cos u) \end{eqnarray}

以上より、頂点の角度\(\hspace{2pt}\large{u}\hspace{2pt}\)に対する立体角\(\hspace{2pt}\large{\Omega}\hspace{2pt}\)の変換式が得られます。

【3】立体角の計算例

本章では、立体角の計算例について解説します。

・球面全体の立体角

球面全体の立体角\(\hspace{2pt}\large{\Omega}\hspace{2pt}\)を求めます。
立体角の定義式(1)から求める場合、半径\(\hspace{2pt}\large{r}\hspace{2pt}\)の球全体の表面積は\(\hspace{2pt}\large{S=4\pi \hspace{1pt} r^2}\hspace{2pt}\)であるため、立体角は以下のように求められます。 $$\large{ \Omega=\frac{4\pi r^2}{r^2}=4\pi[sr]}$$

また、頂点の角度と立体角の関係式(3)から求める場合、\(\hspace{2pt}\large{u=\pi}\hspace{2pt}\)を代入すると、球全体の立体角を求められます。 $$\large{ \Omega=2\pi (1-\cos (\pi)) = 4\pi[sr]}$$

全球の立体角が\(\hspace{2pt}\large{\Omega=4\pi}\hspace{2pt}\)であることから、立体角のとりうる最大値は\(\hspace{2pt}\large{4\pi}\hspace{2pt}\)であることが分かります。

・半球の立体角

半球の立体角\(\hspace{2pt}\large{\Omega}\hspace{2pt}\)を求めます。
立体角の定義式(1)から求める場合、半径\(\hspace{2pt}\large{r}\hspace{2pt}\)の半球の表面積は\(\hspace{2pt}\large{S=2\pi \hspace{1pt} r^2}\hspace{2pt}\)であるため、立体角は以下のように求められます。 $$\large{ \Omega=\frac{2\pi \hspace{1pt}r^2}{r^2}=2\pi[sr]}$$

また、頂点の角度と立体角の関係式(3)から求める場合、\(\displaystyle\hspace{2pt}\large{u=\frac{\pi}{2}}\hspace{2pt}\)を代入すると、半球の立体角を求められます。 $$\large{ \Omega=2\pi \left(1-\cos \left(\frac{\pi}{2}\right)\right) = 2\pi[sr]}$$

・1ステラジアンの表面積

次に、立体角の単位である1ステラジアン(\(\hspace{2pt}\large{1[sr]}\hspace{2pt}\))となる球の表面積を求めます。

半径\(\hspace{2pt}\large{r}\hspace{2pt}\)の球の表面積の\(\hspace{2pt}\large{a}\hspace{2pt}\)倍が1ステラジアンであるとすると、立体角の定義式から以下が成り立ちます。 $$\large{ 1=\frac{S \hspace{1pt} a}{r^2}=\frac{4\pi \hspace{1pt} r^2 \hspace{1pt} a}{r^2}=4 \hspace{1pt}\pi \hspace{1pt}a}$$ したがって、1ステラジアンは球全体の面積の\(\displaystyle\hspace{2pt}\large{\frac{1}{4 \pi}=0.079577...}\hspace{2pt}\)倍の面積であることが分かります。

---