照度とは
本項では、以下の内容について解説します。
- ・光束、照度、光度との関係
- ・照度の求め方
- ・照度の逆二乗則
- ・入射角の余弦法則
- ・水平面照度と鉛直面照度
【1】照度の求め方
照度は、光源に照らされた壁面や物体の明るさを表す量です。
照度の単位は、[lx] または [lm/m2] が使用されます。
照度は、単位面積あたりに入射する光束により求められます。
光束とは、光源から放出される光のエネルギー量を、人の目に感じる明るさに変換した量です。(光のエネルギーと人の感じる明るさの変換については別の記事で解説しています。)
【1-1】光束、照度、光度との関係
ここで、図1に光束、照度、光度の関係を示します。
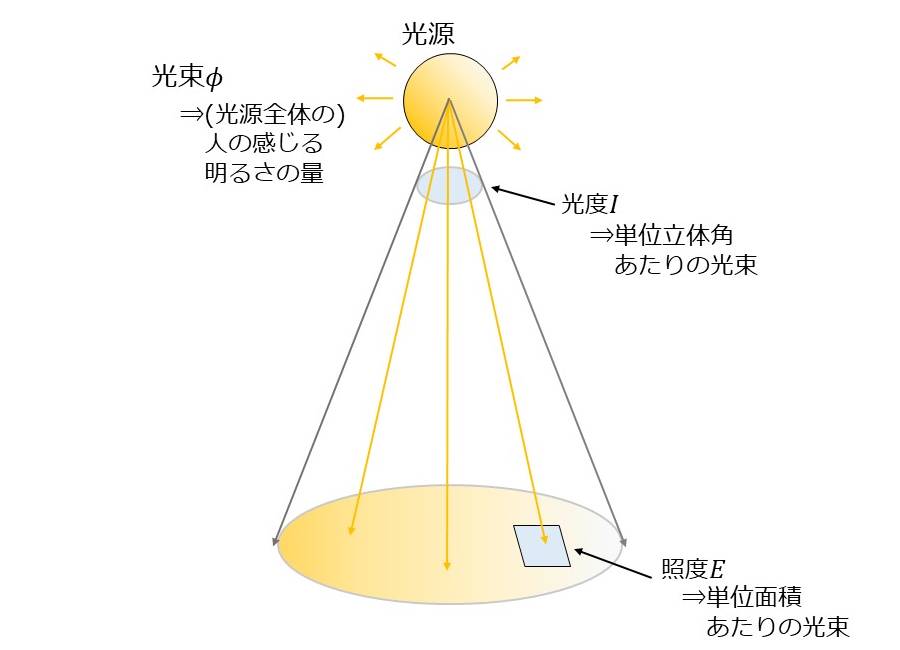
光束は、光源から放出される光の明るさの量を表す値です。
光度とは、単位立体角あたりの光束を表します。光度は、光源がどの方向にどれだけの明るさかを表す値です。
照度は、光源に照らされた面の単位面積あたりの明るさを表しています。
光度と照度の違いとして、光度は特定の角度(立体角)内の明るさであるため、光源の特性によってのみ決定される値です。
一方、照度は照らされた面積あたりの値であるため、光源からの距離や、入射光との角度によって値が変わります。
照度の光源からの距離との関係(照度の逆二乗則)や、入射光の角度との関係(入射角の余弦法則)については、本ページに後述しています。
【1-2】照度の求め方
微小面積\(\hspace{2pt}\large{dS}\hspace{2pt}\)に入射する光束が\(\hspace{2pt}\large{d\phi}\hspace{2pt}\)であるとき、照度\(\hspace{2pt}\large{E}\hspace{2pt}\)は(1)式のように求められます。
また、面積\(\hspace{2pt}\large{S}\hspace{2pt}\)に入射する光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)が一様であるとき、照度Eは以下の式で計算されます。 $$\large{E=\frac{\phi}{S}\hspace{20pt}(2)}$$
【補足】光の明るさを表す用語の一覧
光の明るさを表現する用語として照度、光度の他にも光束発散度や輝度などの値が使用されます。 参考として、以下の表1に意味や使用例の一覧を示します。
【2】照度の逆二乗則
点光源から放出される光の照度は、距離の二乗に反比例して減少するという性質があります。
実際の照明は大きさがゼロではありませんが、照明の大きさが観測距離に比べて十分に小さい場合、点光源と考えて照度を求めます。
点光源の光度を\(\large{\hspace{2pt}I\hspace{2pt}}\)[lm/sr]、光源からの距離を\(\large{\hspace{2pt}R\hspace{2pt}}\)[m]とすると、照度E\(\hspace{2pt}\large{\mathrm{[lm/m^2]}}\hspace{2pt}\)は以下の関係で表現することができます。
先述したように、光度とは単位立体角あたりの光束を表します。光度は、光源がどの方向にどれだけの明るさかを持つかを表す値です。
【2-1】照度の逆二乗則の導出
ここで、照度の逆二乗則(3)式の導出を行います。
図2のように、全方向に一様な光度\(\large{\hspace{2pt}I\hspace{2pt}}\)[lm/sr] を放射する点光源について考えます。
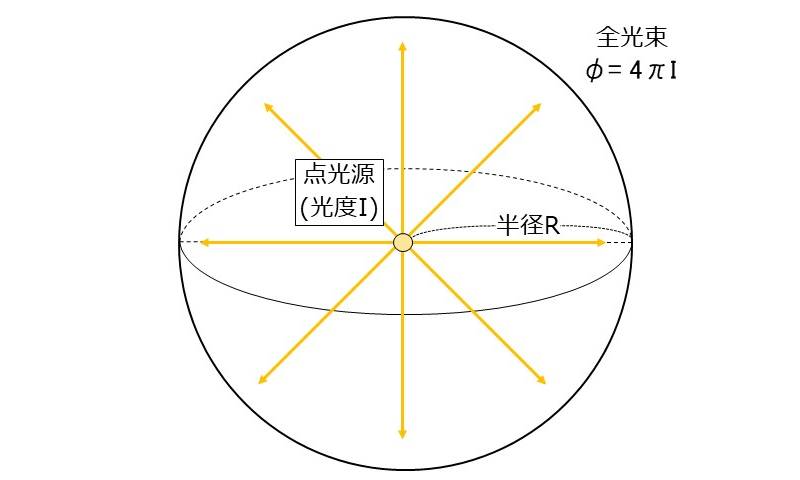
このとき、半径\(\large{\hspace{2pt}R\hspace{2pt}}\)の球面上での全光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)[lm] と光度\(\large{\hspace{2pt}I\hspace{2pt}}\)[lm/sr] の関係を求めます。
光度\(\hspace{2pt}\large{I}\hspace{2pt}\)は球面上で一様な分布であるため、球面上での全光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)と球面の立体角\(\hspace{2pt}\large{\Omega}\hspace{2pt}\)について以下の式が成り立ちます。
$$\large{I = \frac{\phi}{\Omega}}$$ 球面全体の立体角は\(\hspace{2pt}\large{\Omega=4\pi}\hspace{2pt}\)であるため、球面上の全光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)は以下のようになります。 $$\large{\phi = 4\pi I}$$
ここで、球面上における照度Eは、全光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)が球面の表面積\(\hspace{2pt}\large{4\pi R^2}\hspace{2pt}\)に入射していると考えられるので、(2)式から照度Eと全光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)の関係は以下のように求められます。 \begin{eqnarray} \large E&\large =&\large \frac{\phi}{4\pi R^2}\\[0.7em] \large &\large =&\large \frac{4\pi I}{4\pi R^2}\\[0.7em] \large &\large =&\large \frac{I}{R^2} \end{eqnarray} 上式から、点光源から放射される光の照度は、光度に比例し、距離Rの二乗に反比例することが分かります。
【2-2】凸レンズや凹面鏡による平行光の照度
点光源と見なせる照明では、照度は逆二乗則にしたがって距離\(\hspace{2pt}\large{R}\hspace{2pt}\)の二乗に反比例し減少します。
一方、凸レンズや凹面鏡の屈折の作用を利用し、光が平行に伝搬するように屈折させると、光が拡散されないため距離によらず照度は一定となります。
図3に示すように、凸レンズの焦点位置\(\hspace{2pt}\large{F}\hspace{2pt}\)に光源を置くと、レンズを通過した光は平行光となります。
また、凹面鏡の場合も同様に、焦点位置\(\hspace{2pt}\large{F}\hspace{2pt}\)に光源を置くと、鏡面に反射された光は平行光となります。
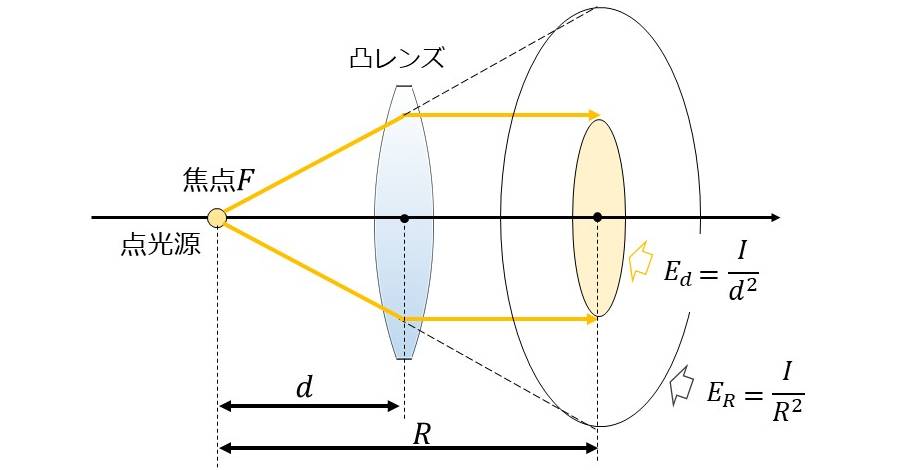
レンズを使用しない場合は、照度\(\hspace{2pt}\large{E_R}\hspace{2pt}\)は逆二乗則にしたがって距離\(\hspace{2pt}\large{R}\hspace{2pt}\)の二乗によって減少します。
$$\large{E_R=\frac{I}{R^2}}$$
一方、レンズの焦点に点光源を配置した場合、レンズを通過した後、照度\(\hspace{2pt}\large{E_d}\hspace{2pt}\)は一定となり、点光源とレンズの間隔\(\hspace{2pt}\large{d}\hspace{2pt}\)によって照度が決まります。
$$\large{E_d=\frac{I}{d^2}}$$
【3】入射角の余弦法則
照度\(\large{\hspace{2pt}E\hspace{2pt}}\)は入射面の面積あたりに入射する光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)によって求められます。
入射する光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)に対して入射面が角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)だけ傾いている場合、照度\(\hspace{2pt}\large{E}\hspace{2pt}\)は入射角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)の余弦(\(\hspace{2pt}\large{\cos \theta}\hspace{2pt}\))に比例します。
このような法則を入射角の余弦法則といいます。
入射面に垂直に入射したときの照度を\(\hspace{2pt}\large{E_0}\hspace{2pt}\)、入射角を\(\hspace{2pt}\large{\theta}\hspace{2pt}\)とすると、入射角の余弦法則は以下の式により表されます。
【3-1】入射角の余弦法則の導出
入射角の余弦法則は以下のように確認できます。
図4のように、入射面に対して垂直に光が入射した場合と、角度\(\large{\hspace{2pt}\theta\hspace{2pt}}\)で入射した場合を比較します。
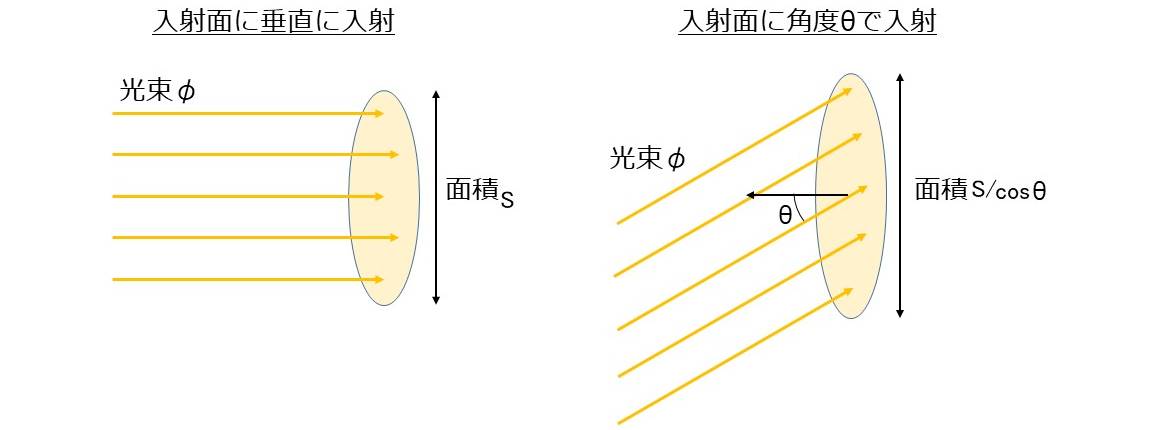
図4の左側のように、面積\(\large{\hspace{2pt}S\hspace{2pt}}\)に光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)が垂直に入射しているとすると、照度\(\hspace{2pt}\large{E_0}\hspace{2pt}\)は以下のように求められます。 $$\large{E_0=\frac{\phi}{S}}$$
一方で図4の右側のように、光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)が角度\(\large{\hspace{2pt}\theta\hspace{2pt}}\)で入射した場合、光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)が入射する面積は、\(\hspace{2pt}\large{S/\cos \theta}\hspace{2pt}\)となります。したがって、照度\(\hspace{2pt}\large{E}\hspace{2pt}\)は以下の式で表せます。 $$\large{E=\frac{\phi \cos \theta}{S}=E_0 \cos \theta \hspace{20pt}(4)}$$
(4)式より、入射角\(\large{\hspace{2pt}\theta\hspace{2pt}}\)に対して照度Eが\(\hspace{2pt}\large{\cos \theta}\hspace{2pt}\)に比例して減少することが分かります。
【3-2】水平面照度と鉛直面照度
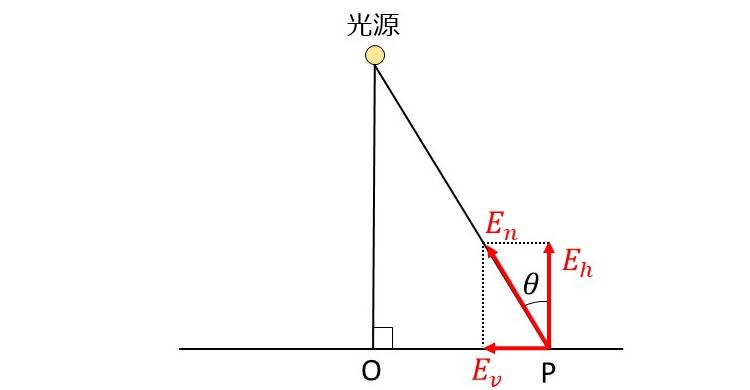
入射角の余弦法則によって求められる照度は、入射面に対して垂直方向の照度であり、水平面照度\(\hspace{2pt}\large{E_h}\hspace{2pt}\)といいます。
一般的に照度という場合は、この水平面照度のことを指します。
また、照射面の入射角に対して平行な方向の照度を、鉛直面照度\(\hspace{2pt}\large{E_v}\hspace{2pt}\)といいます。鉛直面照度を求める場合は、入射角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)に対して\(\hspace{2pt}\large{E_v=E_0\sin \theta}\hspace{2pt}\)から得られます。
図5に点光源からの光が角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)で点\(\hspace{2pt}\large{P}\hspace{2pt}\)に入射したときの水平面照度\(\hspace{2pt}\large{E_h}\hspace{2pt}\)と鉛直面照度\(\hspace{2pt}\large{E_v}\hspace{2pt}\)の関係を示します。
図中\(\hspace{2pt}\large{E_n}\hspace{2pt}\)は、点\(\hspace{2pt}\large{P}\hspace{2pt}\)から光源に向かう方向に垂直な面の照度を表し、法線照度\(\hspace{2pt}\large{E_n}\hspace{2pt}\)といいます。