点光源の照度計算ツール
点光源に照らされた面の照度を逐点法により計算するツールです。
点光源による法線照度 En, 水平面照度 Eh, 鉛直面照度 Ev を簡易に計算できます。
本計算ツールは、2次元平面と3次元空間の2種類を作成しています。
点光源の照度計算 | 2次元平面
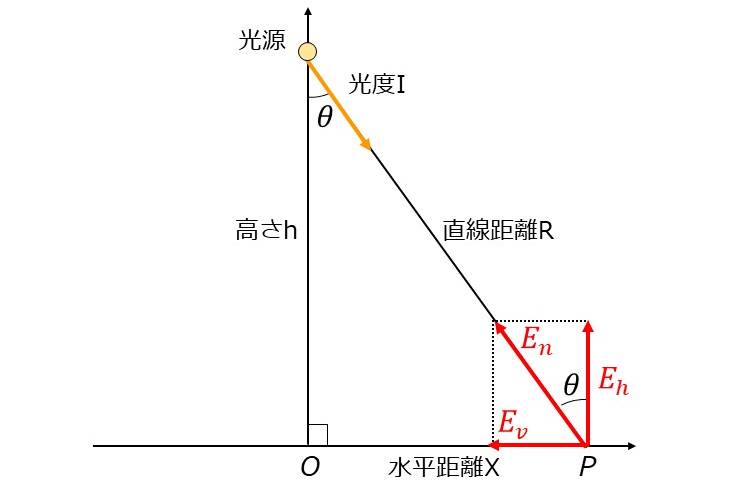
本ツールは、図1のように2次元平面に点光源がある場合の照度を計算するツールです。
原点O から高さ h の位置に光度 I の点光源があるとき、直線距離 R, 水平距離X, 角度θ の位置の点Pの照度を計算します。
【光源の設定】
◆点光源の光度\(\hspace{2pt}\large{I}\hspace{2pt}\)
【照度の計算位置の設定】
◆直線距離R
◆角度θ [°]
【出力の設定】
出力値の小数点以下の桁数
| 光源の光度\(\hspace{2pt}\large{I}\hspace{2pt}\) | ||
|---|---|---|
| 法線照度\(\hspace{2pt}\large{E_n}\hspace{2pt}\) | 水平面照度\(\hspace{2pt}\large{E_h}\hspace{2pt}\) | 鉛直面照度\(\hspace{2pt}\large{E_v}\hspace{2pt}\) |
|---|---|---|
(※当サイトの提供する計算結果や情報については一切責任は負いません。)
照度計算ツールの使い方
【光源の設定】では、点光源の光度\(\hspace{2pt}\large{I}\hspace{2pt}\)の大きさと、入力する光度の単位を設定します。
【照度の計算位置の設定】では、照度を計算する点Pの位置を設定します。
点Pの位置の指定方法には『直線距離R, 角度θ』、『高さh, 角度θ』、『高さh, 水平距離X』の3種類がありますので、プルダウンで選択してください。
角度は度数法[°]で指定してください。また、距離の単位はプルダウンで選択できます。
【出力の設定】では、算出する照度の単位を設定してください。
『出力値の小数点以下の桁数』では、指定された桁数より1つ小さい桁で四捨五入を行い出力します。
上記の設定後、『照度計算の実行』により結果を出力します。
点光源の照度計算 | 3次元空間
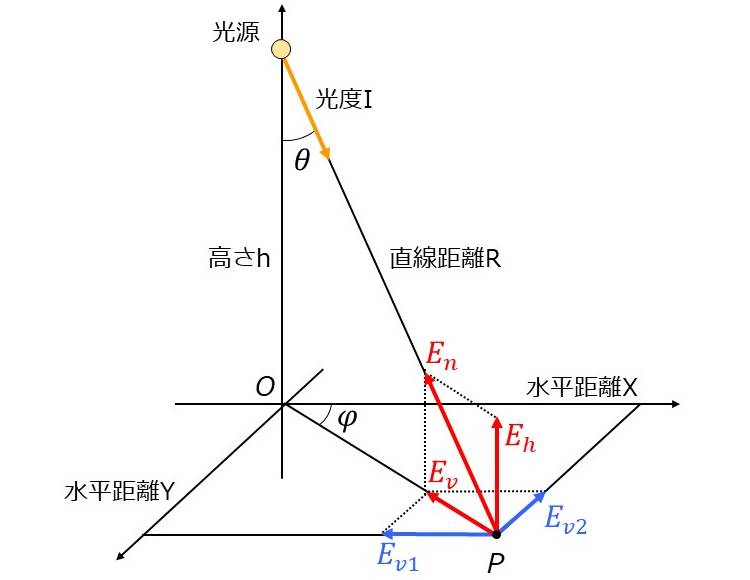
本計算ツールは、図2のような3次元空間に点光源がある場合の照度を計算するツールです。
原点\(\hspace{2pt}\large{O}\hspace{2pt}\) から高さ\(\hspace{2pt}\large{h}\hspace{2pt}\) に光度\(\hspace{2pt}\large{I}\hspace{2pt}\) の点光源がある場合の、直線距離\(\hspace{2pt}\large{R}\hspace{2pt}\)、鉛直角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)、水平角\(\hspace{2pt}\large{\phi}\hspace{2pt}\) の位置の照度を計算します。
3次元空間の場合、法線照度\(\hspace{2pt}\large{E_n}\hspace{2pt}\) , 水平面照度\(\hspace{2pt}\large{E_h}\hspace{2pt}\) , 鉛直面照度\(\hspace{2pt}\large{E_v}\hspace{2pt}\) に加えて、鉛直面照度のX方向成分\(\hspace{2pt}\large{E_{v1}}\hspace{2pt}\) と鉛直面照度のY方向成分\(\hspace{2pt}\large{E_{v2}}\hspace{2pt}\) も計算します。
【光源の設定】
◆点光源の光度\(\hspace{2pt}\large{I}\hspace{2pt}\)
【照度の計算位置の設定】
◆直線距離R
◆鉛直角θ [°]
◆水平画φ [°]
【出力の設定】
出力値の小数点以下の桁数
| 光源の光度\(\hspace{2pt}\large{I}\hspace{2pt}\) | |||
|---|---|---|---|
| 法線照度\(\hspace{2pt}\large{E_n}\hspace{2pt}\) | 水平面照度\(\hspace{2pt}\large{E_h}\hspace{2pt}\) | 鉛直面照度\(\hspace{2pt}\large{E_v}\hspace{2pt}\) |
|---|---|---|
| 鉛直面照度 X軸成分\(\hspace{2pt}\large{E_{v1}}\hspace{2pt}\) |
鉛直面照度 Y軸成分\(\hspace{2pt}\large{E_{v2}}\hspace{2pt}\) |
|
|---|---|---|
(※当サイトの提供する計算結果や情報については一切責任は負いません。)
照度計算ツールの使い方
【光源の設定】では、点光源の光度\(\hspace{2pt}\large{I}\hspace{2pt}\)の大きさと、入力する光度の単位を設定します。
【照度の計算位置の設定】では、照度を計算する点Pの位置を設定します。
点Pの位置の指定方法には『直線距離R, 鉛直角θ, 水平角φ』、『高さh, 鉛直角θ, 水平角φ』、『高さh, 水平面位置(X,Y)』の3種類がありますので、プルダウンで選択してください。
角度は度数法[°]で指定してください。また、距離の単位はプルダウンで選択できます。
【出力の設定】では、算出する照度の単位を設定してください。
『出力値の小数点以下の桁数』では、指定された桁数より1つ小さい桁で四捨五入を行い出力します。
上記の設定後、『照度計算の実行』により結果を出力します。
照度の計算方法
本章では、計算ツール内の照度計算の方法について説明します。
法線照度 | 照度の逆二乗則
点光源から照らされる面の照度は、照度の逆二乗則により計算されます。
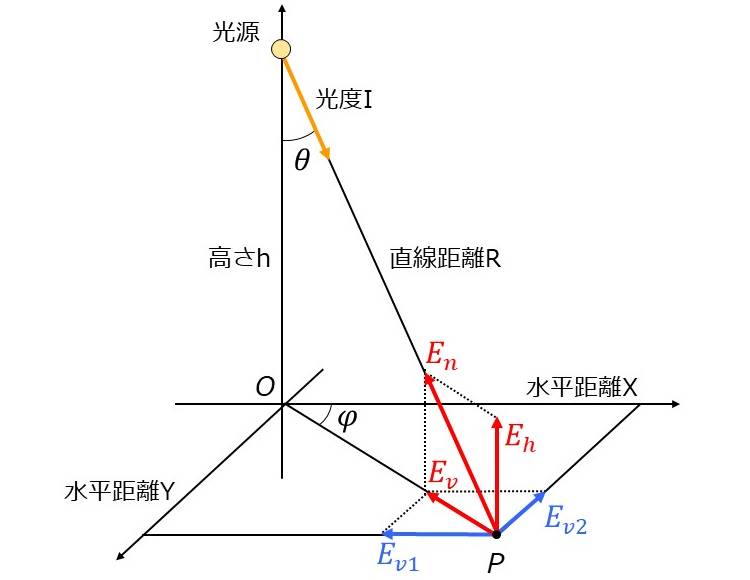
例えば、図3のように光度\(\hspace{2pt}\large{I}\hspace{2pt}\)の点光源から直線距離\(\hspace{2pt}\large{R}\hspace{2pt}\)だけ離れた点\(\hspace{2pt}\large{P}\hspace{2pt}\)における照度(法線照度\(\hspace{2pt}\large{E_n}\hspace{2pt}\))は、光度\(\hspace{2pt}\large{I}\hspace{2pt}\)に比例し、距離\(\hspace{2pt}\large{R}\hspace{2pt}\)の逆二乗に反比例する式により計算されます。
水平面照度と鉛直面照度 | 入射角の余弦法則
入射面に対して垂直方向の照度は、入射角の余弦に比例して変化します。この法則を入射角の余弦法則といいます。
図3の照度\(\hspace{2pt}\large{E_h}\hspace{2pt}\)は、この入射角の余弦法則から計算される照度であり、水平面照度といいます。
また、図3の\(\hspace{2pt}\large{E_v}\hspace{2pt}\)は、法線照度の正弦成分で計算され、鉛直面照度といいます。
鉛直面照度のX軸成分とY軸成分
3次元の空間で照度を考えた場合、鉛直面照度\(\hspace{2pt}\large{E_v}\hspace{2pt}\)にはX軸成分とY軸成分があります。
図3より水平角\(\hspace{2pt}\large{\phi}\hspace{2pt}\)だけ角度のある場合の鉛直面照度\(\hspace{2pt}\large{E_v}\hspace{2pt}\)の、X軸成分\(\hspace{2pt}\large{E_{v1}}\hspace{2pt}\)とY軸成分\(\hspace{2pt}\large{E_{v2}}\hspace{2pt}\)は以下の式により計算されます。
参考文献
・(1)社団法人 照明学会『大学課程 照明工学(新版)』株式会社オーム社, 平成17年3月31日 第1版第8刷 発行,4章 照明計算 pp86