光度とは
本項では、以下の内容について解説します。
- ・光度の求め方
- ・照度、輝度との関係式
- ・放射強度と光度の違い
【1】光度とは
光度は、光源から特定の方向へ放出される光の明るさを表現する値です。
光度の単位は、カンデラ[cd] が使用されます。1[cd]=1[lm/sr] であるため、1カンデラは1ステラジアンに1ルーメンの光が放出されていることを表します。
ステラジアン[sr] は、球の中心からの広がりの大きさを表す立体角の単位です。
また、ルーメン[lm] は光のエネルギー量を、人の感じる明るさに変換した単位です。(光のエネルギーから人の感じる明るさへの変換については別のページで解説しています。)
【1-1】光度の求め方
光度\(\hspace{2pt}\large{I}\hspace{2pt}\)は、『特定の方向へ放出される単位立体角あたりの光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)』により求められます。
光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)とは、単位時間にある面積を通過する光のエネルギー量を、人の感じる明るさに変換した値です。
図1に点光源から微小立体角\(\hspace{2pt}\large{d\Omega}\hspace{2pt}\)中に光束\(\hspace{2pt}\large{d\phi}\hspace{2pt}\)が放出される様子を図示します。
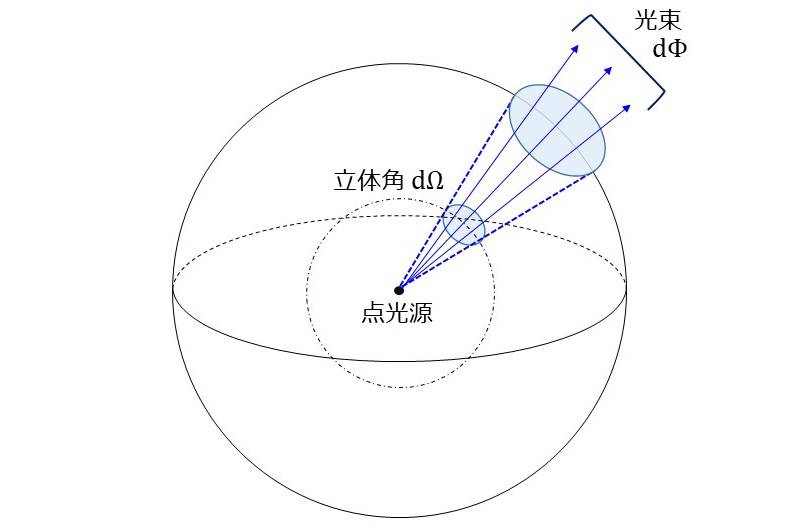
図1のように、微小立体角\(\hspace{2pt}\large{d\Omega}\hspace{2pt}\)中の光束が\(\hspace{2pt}\large{d\phi}\hspace{2pt}\)であるとき、光度\(\hspace{2pt}\large{I}\hspace{2pt}\)は(1)式のように表せます。
また、立体角\(\hspace{2pt}\large{\Omega}\hspace{2pt}\)中の光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)が一様である場合は、以下のように表せます。 $$\large{I = \frac{\phi}{\Omega}\hspace{20pt}(2)}$$
例えば、図1の点光源から放出される光束が一様であるときの、光束と光度の関係を求めます。
図1の点光源から、あらゆる方向に放出される光束を、全て足し合わせた光束の大きさが\(\hspace{2pt}\large{\phi}\hspace{2pt}\)であるとします。
また、点光源から放出される光の光度\(\hspace{2pt}\large{I}\hspace{2pt}\)が、全ての方向に対して一様であるとします。
ここで、球全体の立体角は\(\hspace{2pt}\large{4 \pi}\hspace{2pt}\)[sr] と求められます。(2)式に代入すると、光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)と光度\(\hspace{2pt}\large{I}\hspace{2pt}\)の関係は以下のように求められます。
$$\large{I = \frac{\phi}{4 \pi}}$$
【1-2】光度と光束の違い
光度と同じように明るさを表現する用語として、『光束』が使われることがあります。
光束は、ある面積を通過する光の明るさを表現する値です。
例えば、照明機器の全体がどれだけの明るさかを表現するために、光束の値が使用されます。
一方、照明機器の明るさは見る方向によって変化するため、照明全体の明るさだけでなく、どの方向にどれだけ明るいかも重要な要素となります。
光度は、光源がどの方向に、どれだけ明るいかを表現するために使用されます。
例えば、照明機器では角度による光度の変化をグラフで表し、明るさが方向によってどのように変化するかを表記します。このような光度の空間内の分布を表すグラフを配光曲線といいます。
【補足】光の明るさを表す用語の一覧
光の明るさを表現する用語として光束や光度の他にも、照度や輝度などの用語が使用されます。 参考として、以下の表1に意味や使用例などを示します。
【2】光度と照度、輝度の関係式
本章では、光度と密接な関係にある照度、輝度との関係式について解説します。
【2-1】光度と照度の関係式
照度とは、単位面積あたりに入射する光束により計算される量です。
光度と照度の違いは、光度は特定の方向から見た光源の明るさを表し、照度は光源に照らされた壁面や物体の明るさを表す点にあります。
照度は1m2あたりに入射する光束[lm] により定義されます。また、照度の単位は [lm/m2] が使用されます。
光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)の光が面積\(\hspace{2pt}\large{S}\hspace{2pt}\)の面に入射しているとき、照度\(\hspace{2pt}\large{E}\hspace{2pt}\)は以下のように表されます。
ここで、点光源を例として光度と照度の関係を求めます。
前章の点光源の光束と光度の関係から、点光源から光度\(\hspace{2pt}\large{I}\hspace{2pt}\)の光が放出されているとき、全光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)は以下のようになります。 $$\large{\phi = 4 \pi I}$$ また、半径\(\hspace{2pt}\large{r}\hspace{2pt}\)の球の表面積は\(\hspace{2pt}\large{S=4 \pi r^2 }\hspace{2pt}\)と表されます。(3)式に点光源の全光束\(\hspace{2pt}\large{\phi}\hspace{2pt}\)と表面積\(\hspace{2pt}\large{S}\hspace{2pt}\)を入れて計算すると、照度\(\hspace{2pt}\large{E}\hspace{2pt}\)は以下の関係を満たします。
上式より、照度\(\hspace{2pt}\large{E}\hspace{2pt}\)は光度\(\hspace{2pt}\large{I}\hspace{2pt}\)に対して距離\(\hspace{2pt}\large{r}\hspace{2pt}\)の二乗で減少する関係にあることが分かります。
【2-2】光度と輝度の関係式
輝度とは、ある面積をもった光源に対して、見かけの面積あたりの光度を表現する値です。
輝度は、ディスプレイなど面積のある光源から照射される光の明るさを表現するために使用されます。
光度と輝度の違いは、光度は特定の方向から見た光源の明るさを表し、輝度は見る方向によって光源の面積が変化することを考慮した明るさを表す点にあります。
光度も輝度も光源の明るさを表す用語ですが、光源の見かけの面積を計算にいれるかどうかが異なります。
輝度は1m2あたりに放出される光度[cd] により定義されます。また、輝度の単位は [lm/(sr・m2)] が使用されます。
光源面の法線から角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)の方向の光度が\(\hspace{2pt}\large{I_\theta}\hspace{2pt}\)であるとき、見かけの面積\(\hspace{2pt}\large{S'=S \cos \theta}\hspace{2pt}\)から放出される輝度\(\hspace{2pt}\large{L_\theta}\hspace{2pt}\)は以下の式で表されます。
【3】放射強度と光度
放射強度と光度の違いは、対象とする現象が物理的な光のエネルギーなのか、人の感じる明るさなのかによって使い分けられる点にあります。
放射強度とは、ある方向に単位立体角あたりの放射束(単位時間あたりの光のエネルギー)を表します。 つまり、放射強度は単位立体角あたりの光の物理的なエネルギー量を表します。
一方、光度は、物理的なエネルギーの量である放射強度を、人の眼で感じる明るさに変換した量です。 照明機器やディスプレイなど人の眼で観察することを前提とした現象を扱うときに使用されます。
放射強度\(\hspace{2pt}\large{I}\hspace{2pt}\)の定義式は、微小立体角\(\hspace{2pt}\large{d\Omega}\hspace{2pt}\) 中の放射束が\(\hspace{2pt}\large{d\phi}\hspace{2pt}\) であるとすると、以下のように表されます。
放射強度の式は、光度の定義式(1)と同じ形式で書き表されます。
(1)式と(3)式で異なる点は、光のエネルギーを表す\(\hspace{2pt}\large{\phi}\hspace{2pt}\)が物理的なエネルギーを意味する放射束か、人に感じられる明るさを意味する光束かの点にあります。
放射強度は1ステラジアンあたりの光エネルギー量[W] を意味するため、放射強度の単位には [W/sr] を使用します。