累乗, 累乗根の大小比較

『\(\large{\sqrt{2}}\) と \(\large{\sqrt[3]{4}}\)』や『\(\large{2^{30}}\) と \(\large{3^{20}}\)』などの大小関係は、指数法則や指数関数のグラフの特徴を利用し決定することができます。

本項では、指数の性質を利用し、累乗や累乗根の大小関係を求める問題について解説します。

【1】底をそろえて比較する場合

本章では、指数で表記された値の大小関係を、底をそろえて比較する問題について解説します。

【1-1】累乗根の大小関係(底が1より大きい場合)

まず、以下のような問題について考えます。

累乗根の大小関係を調べるときは、『底をそろえて指数を比較する』ことが基本になります。

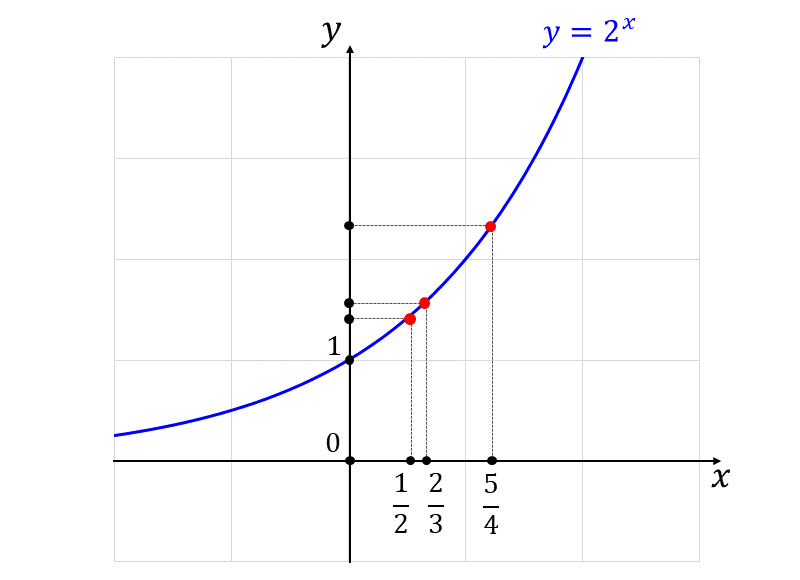
まず、与えられた3つの値の底を指数法則を利用して \(\large{2}\) にそろえます。 $$\large{\sqrt{2} = 2^\frac{1}{2}}$$ $$\large{\hspace{5pt}\sqrt[3]{4} =2^\frac{2}{3}}$$ $$\large{\hspace{5pt}\sqrt[4]{32} =2^\frac{5}{4}}$$

ここで、指数関数のグラフから、\(\large{y=a^x}\) の底が \(\large{1}\) より大きければ、単調増加 (\(\large{x}\)の値が大きくなれば、常に\(\large{y}\)の値が大きくなる) の性質があります。

すなわち、底を \(\large{2}\) でそろえることで、指数 \(\large{\boldsymbol{x}}\) の大小関係が、\(\large{\boldsymbol{y}}\) の値の大小関係と等しくなります。

問題で与えられた3つの値の指数の大小関係は、 $$\large{\frac{1}{2} < \frac{2}{3} < \frac{5}{4}}$$ であるため、 $$\large{\sqrt{2} < \sqrt[3]{4} < \sqrt[4]{32}}$$ となります。

以下に、\(\large{y=2^x}\) の\(\large{x=\frac{1}{2}, \hspace{5pt}\frac{2}{3}, \hspace{5pt}\frac{5}{4}}\) の値をプロットした図を示します。

【1-2】累乗根の大小関係(底が 0 < a < 1 の場合)

次に、以下のような問題を考えます。

先ほどと同様に、累乗根の大小関係を調べるときは、『底をそろえて指数を比較』します。

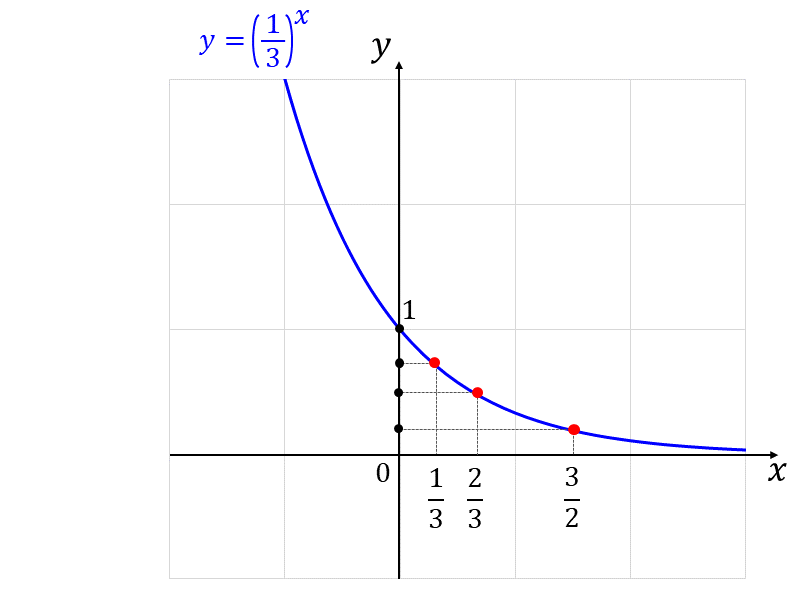
まず、与えられた値の底を指数法則を利用して \(\displaystyle \large{\frac{1}{3}}\) にそろえます。 $$\large{\sqrt[3]{\frac{1}{3}} = \left(\frac{1}{3} \right)^\frac{1}{3}}$$ $$\large{\hspace{5pt}\sqrt[3]{\frac{1}{9}}= \left(\frac{1}{3} \right)^\frac{2}{3}}$$ $$\large{\hspace{5pt}\sqrt{\frac{1}{27}} = \left(\frac{1}{3} \right)^\frac{3}{2}}$$

指数関数のグラフから、\(\large{y=a^x}\) の底が\(\large{0 < a < 1 }\)の場合、単調減少 (\(\large{x}\)の値が大きくなれば、常に\(\large{y}\)の値が小さくなる) の性質があります。

したがって、問題で与えられた3つの値の指数の大小関係は、 $$\large{\frac{1}{3} < \frac{2}{3} < \frac{3}{2}}$$ であるため、底の \(\displaystyle \large{\frac{1}{3}}\) が\(\large{1}\)より小さいことから、指数の大小関係を反転させ、以下のようになります。 $$\large{\sqrt{\frac{1}{27}} < \sqrt[3]{\frac{1}{9}} < \sqrt[3]{\frac{1}{3}}}$$

以下に、\(\displaystyle \large{y=\left(\frac{1}{3} \right)^x}\) の \(\displaystyle \large{x=\frac{1}{3}, \hspace{5pt}\frac{2}{3}, \hspace{5pt}\frac{3}{2}}\) の値をプロットした図を示します。

【2】底が異なる場合の大小比較

本章では、底が異なる場合の大小関係の問題について解説します。

【2-1】底が異なる場合の大小比較(1)

次に、以下のような問題をについて考えます。

まず、与えられた値を \(\large{a^x}\) の表記に書き換えて整理します。 $$\large{\sqrt{3} = 3^\frac{1}{2}}$$ $$\large{\sqrt[3]{4} = 2^\frac{2}{3}}$$ $$\large{\sqrt[6]{5} = 5^\frac{1}{6}}$$ 上記のように、3つの値は底が異なるため、『底をそろえて指数を比較する』ことができません。
このような場合は、『指数をそろえて底を比較する』ことで大小関係を求められることがあります。

問題で与えれた値は\(\large{6}\)乗することで、整数の値にすることができます。
指数法則を利用して計算すると、以下のようになります。 $$\large{(\sqrt{3})^6 = 3^\frac{6}{2}=27}$$ $$\large{(\sqrt[3]{4})^6 = 2^\frac{12}{3}=16}$$ $$\large{(\sqrt[6]{5})^6 = 5^\frac{6}{6}}=5$$

したがって、 \(\large{5 < 16 < 27 }\) であることから、以下の関係が成り立ちます。 $$\large{(\sqrt[6]{5})^6 < (\sqrt[3]{4})^6 < (\sqrt{3})^6}$$

このとき、\(\large{0}\) より大きい数は\(\large{6}\)乗する前後で大小関係が一致するため、与えられた数の大小関係は以下のようになります。 $$\large{\sqrt[6]{5} < \sqrt[3]{4} < \sqrt{3}}$$

【2-2】底が異なる場合の大小比較(2)

次に、以下のような問題について考えます。

与えられた値は底が異なるため、『底をそろえて指数を比較する』ことができません。
ここでは、『指数をそろえて底を比較する』ことで大小関係を求めます。

与えられた値の指数は、\(\large{10}\) の倍数であるため、指数法則を利用して、指数を \(\large{10}\) にそろえて大小を比較します。

指数法則 \(\large{(a^m)^n = a^{mn}}\) を用いて \(\large{2^{30},\hspace{2pt} 3^{20}}\) を変形すると、以下のようになります。

$$\large{2^{30} = 2^{3 \times 10}=(2^3)^{10}=8^{10}}$$ $$\large{3^{20} = 3^{2 \times 10}=(3^2)^{10}=9^{10}}$$

したがって、 \(\large{5^{10} < 8^{10} < 9^{10} }\) であることから、与えられた数の大小関係は以下のようになります。 $$\large{5^{10} < 2^{30} < 3^{20}}$$

---