対数不等式
本項では、『対数不等式の問題と解き方』 について解説します。
【1】対数不等式の解き方
対数不等式とは、 $$\large{\displaystyle \large{2\log_2 x > \log_2 (3x+4) }}$$ のように対数を含む不等式のことです。
対数不等式を解くときは、以下の 『解法① : 対数の真数を比較』 か 『解法② : 対数の置換』 により解きます。
解法① : 対数の真数を比較
この解法は、対数の底が等しい不等式の真数を比較する方法です。
対数不等式を同じ底\(\large{a}\) である \(\large{\log_a M < \log_a N}\) の式に変形した後、底\(\large{a}\) の大きさによって以下のように真数の不等式とすることができます。
上記のように、底\(\large{a}\) の大きさによって 真数の不等号の向きが変化します。
この『対数の不等号』と『真数の不等号』の向きの関係は、対数関数のグラフから説明することができます。
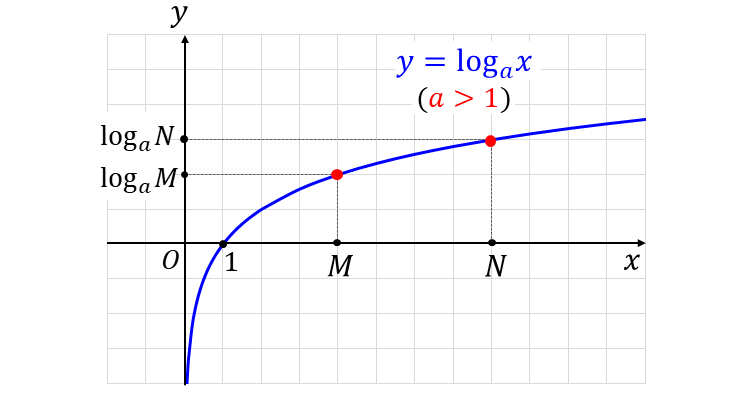
対数関数 \(\large{y=\log_a x}\) は、対数のグラフの特徴より、底が \(\large{1}\) より大きい場合は 単調増加 (\(\large{x}\)が増加すると、\(\large{y}\)も常に増加) の性質があります。
つまり、下図のように \(\large{a > 1}\) のときは対数\(\large{\hspace{3pt}\log_a M,\hspace{1pt}\log_a N\hspace{3pt}}\)の大小関係と、真数\(\large{\hspace{3pt}M,N\hspace{3pt}}\)の大小関係が一致します。
したがって、『対数の不等号』と『真数の不等号』の向きが一致します。
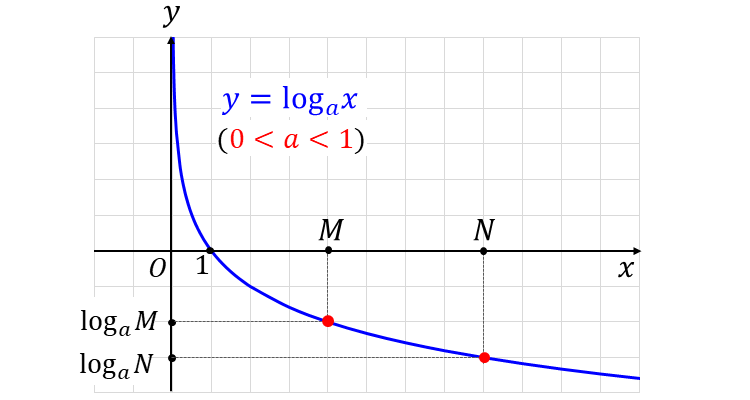
一方、底が \(\large{1}\) より小さい対数関数は 単調減少 (\(\large{x}\)が増加すると、\(\large{y}\)は常に減少) の性質があります。
つまり、下図のように \(\large{0 < a < 1}\) のときは、対数\(\large{\hspace{3pt}\log_a M,\hspace{1pt}\hspace{3pt}\log_a N\hspace{3pt}}\)の大小関係と、真数\(\large{\hspace{3pt}M,N\hspace{3pt}}\)の大小関係は反転します。
したがって、『対数の不等号』と『真数の不等号』の向きが反転します。
対数の真数を比較する問題は、問題(1),(2),(3)で解説しています。
解法② : 対数を置換
対数が2乗されている場合など、対数の真数を両辺で比較できない場合は この方法で解きます。
対数を置換する場合、\(\large{M>0}\) の範囲では、\(\large{\log_a M = X}\) は全ての実数をとることに注意が必要です。
不等式の両辺に \(\large{\log_a M = X}\) をかける場合、\(\large{X}\)が正の場合 と \(\large{X}\)が負の場合 で不等号の向きが変わるため、場合分けが必要になります。(問題(5))
対数を置換する問題は、問題(4),(5)で解説しています。
真数条件と底の条件
対数不等式では 全ての実数\(\large{x}\) で解を求めると、対数が成り立たない範囲が含まれる場合があります。
そのため、対数不等式を解くときは、与えられた対数が真数条件を満たすように 解\(\large{x}\) の成り立つ条件を求めておきます。
真数条件とは、対数が \(\large{p = \log_a M}\) で表されるとき、真数\(\large{M}\) が正となるという条件です。
例えば、以下の対数不等式を解くとします。 $$\large{\log_2 (x-1) > 3 }$$ このとき、真数条件は \(\large{x-1 >0 }\) すなわち \(\large{x >1}\) となります。
また、\(\large{\log_x 2}\) など底に変数含む場合は、以下の底の条件も満たす必要があります。
例えば、\(\large{\log_x 2}\) を含んだ対数不等式では、底の条件から \(\large{x>0,\hspace{5pt} x \neq 1}\) の条件が必要になります。(問題(5))
【2】対数不等式の問題
本章では、以下の(1)~(5)の対数不等式の問題について解説します。
(2) \(\displaystyle \large{2\log_\frac{1}{2} x > \log_\frac{1}{2} (3x+4) }\)
(3) \(\displaystyle \large{\log_a x + \log_a (x-2) < \log_a 3}\)
(4) \(\displaystyle \large{(\log_2 x)^2 - 3 \log_2 x > 4}\)
(5) \(\displaystyle \large{\log_3 x -3\log_x 3 < 2}\)
問題(1) 真数の比較 | 底が1より大きい場合
\(\displaystyle \large{\log_2 (x-1) > 3 }\)
対数不等式を解くときは、まず真数条件を確認します。
対数の真数は正であることから、\(\large{x-1 > 0}\) すなわち、\(\large{ x > 1}\)が成り立ちます。
解法①:真数の比較から、右辺を底が 2 の対数に変形します。 $$\large{3=\log_2 2^3=\log_2 8}$$ よって、与えられた不等式は以下のようになります。 $$\large{\log_2 (x-1) > \log_2 8}$$ 上式は 底が 1 より大きい対数の不等式であり、真数を比較した不等号の向きは一致するため、以下のようになります。 $$\large{x-1 > 8}$$ $$\large{ x > 9}$$ 得られた \(\large{x}\)の範囲と、真数条件\(\large{ x > 1}\) の共通範囲をとると、問題の解は以下となります。 $$\large{x > 9}$$
問題(2) 真数の比較 | 底が1より小さい場合
\(\displaystyle \large{2\log_\frac{1}{2} x > \log_\frac{1}{2} (3x+4) }\)
まず、真数条件を確認します。
対数の真数は正であることから、\(\large{x > 0}\) かつ \(\large{3x+4 > 0}\) が成り立ちます。
2つの不等式の共通範囲をとると、解の存在する範囲は、
$$\large{x > 0}$$
となります。
次に、対数の公式
$$\large{b\log_a M = \log_a M^b}$$
を使用し与えられた式を変形すると、(左辺)\(\large{=2\log_\frac{1}{2} x = \log_\frac{1}{2} x^2}\)
となります。したがって、与えられた不等式は
$$\large{\log_\frac{1}{2} x^2 > \log_\frac{1}{2} (3x+4)}$$
と変形されます。
上式は 底が 1 より小さい対数の不等式であり、真数を比較した不等号の向きは反転するため、以下のようになります。
$$\large{x^2 < 3x+4}$$
$$\large{x^2 -3x -4 < 0}$$
$$\large{(x+1)(x-4) < 0}$$
上記の不等式の解は、\(\large{ -1 < x < 4}\) となります。
ここで、真数条件から解の存在する範囲が \(\large{x > 0}\) であるため、求める解は
$$\large{0 < x < 4}$$
となります。
問題(3) 底が文字の場合
\(\displaystyle \large{\log_a x + \log_a (x-2) < \log_a 3}\)
本問では、式中に底が文字\(\large{a}\) の対数が含まれています。
真数どうしで比較するとき、底の大きさにより不等号の向きが変化するため、文字\(\large{a}\) の大きさで場合分けが必要になります。
まず、真数条件を確認します。
対数の真数は正であることから、\(\large{x > 0}\) かつ \(\large{x-2 > 0}\) となります。
したがって、共有範囲をとると \(\large{x> 2}\) となります。
次に、対数の公式 $$\large{\log_a{MN} = \log_a M+ \log_a N}$$ を使用し 与えられた式を変形すると、 $$\large{\log_a x(x-2) < \log_a 3}$$ ここで、真数どうしを比較して不等式を解くときに、文字\(\large{a}\) の大きさで場合分けをします。
【Ⅰ】\(\large{\boldsymbol{a > 1}}\) の場合
\(\large{a >1}\) のとき、『対数の不等号』 と 『真数の不等号』 の向きは一致するため、 $$\large{x(x-2) < 3}$$ $$\large{x^2 -2x -3 < 0}$$ $$\large{(x+1)(x-3) < 0}$$ したがって、\(\large{x}\) の範囲は \(\large{-1 < x < 3}\) となりますが、真数条件 \(\large{x> 2}\) から、求める解は $$\large{2 < x < 3}$$ となります。
【Ⅱ】\(\large{\boldsymbol{0 < a < 1}}\) の場合
\(\large{0 < a < 1}\) のとき、『対数の不等号』 と 『真数の不等号』 の向きは反転するため、 $$\large{x(x-2) > 3}$$ $$\large{x^2 -2x -3 > 0}$$ $$\large{(x+1)(x-3) > 0}$$ したがって、\(\large{x}\) の範囲は \(\large{x < -1, x > 3}\) となりますが、真数条件 \(\large{x> 2}\) から、求める解は $$\large{x>3}$$ となります。
したがって、問題の不等式の解は、
\(\large{a >1}\) のとき \(\large{2 < x < 3}\)、\(\large{0 < a < 1}\) のとき \(\large{x>3}\)
となります。
問題(4) 対数の置換
\(\displaystyle \large{(\log_2 x)^2 - 3 \log_2 x > 4}\)
まず、真数条件を確認します。
対数の真数は正であることから、\(\large{x > 0}\) が成り立ちます。
ここで、問題の不等式は 真数を単純に比較できないため、解法②:対数の置換を使用します。
\(\large{\log_2 x = X}\) とおくと、与えられた不等式は以下のようになります。 $$\large{X^2 -3X > 4 }$$ $$\large{X^2 -3X -4 > 0}$$ $$\large{(X+1)(X-4) > 0}$$
上記の不等式の解は、\(\large{X < -1, X > 4}\) となります。
ここで、\(\large{\log_2 x = X}\) から不等式を \(\large{x}\) の式に変形すると、
$$\large{\log_2 x < -1, \log_2 x >4}$$
$$\large{\log_2 x < \log_2 2^{-1}, \log_2 x >\log_2 2^4}$$
ここで、上式は 底が 1 より大きい対数の不等式であり、真数を比較した不等号の向きは一致するため、以下のようになります。
$$\large{x < 2^{-1}, x > 2^4}$$
$$\large{x < \frac{1}{2}, x > 16}$$
また、真数条件 \(\large{x > 0}\) との共通範囲をとると、解は以下の不等式になります。
$$\large{0 < x < \frac{1}{2}, x > 16}$$
問題(5) 対数を置換 | 底に変数xが含まれる場合
\(\displaystyle \large{\log_3 x -3\log_x 3 < 2}\)
対数の真数は正であることから、真数条件は \(\large{x > 0}\) となります。
また、与えられた対数不等式には、底に変数 \(\large{x}\) が含まれています。
底に変数が含まれている場合は、真数条件に加えて、底の条件も考慮する必要があります。
・\(\large{a > 0, \hspace{5pt} a \neq 1}\) (底の条件)
・\(\large{M > 0}\) (真数条件)
\(\large{\log_x 3}\) の底の条件と真数条件から、与えられた式が成り立つ \(\large{x}\) の範囲は \(\large{x>0,x\neq 1}\) となります。
次に、対数の底がそろっていないため、底の変換公式から底の値をそろえます。
底の変換公式 \(\displaystyle \large {\log_a b = \frac{1}{\log_b a}}\) から
$$\large{\log_x 3 = \frac{1}{\log_3 x}}$$
したがって、不等式を変形すると、
$$\large{\log_3 x -3 \frac{1}{\log_3 x} < 2\hspace{10pt}(1)}$$
となります。
(1)式は両辺に \(\large{\log_3 x}\) をかけることで二次不等式として解くことができます。
このとき、\(\large{\log_3 x}\) は \(\large{x}\) の値により正負が変わり、不等号の向きも変わるため、場合分けをして解きます。
【Ⅰ】\(\large{\boldsymbol{\log_3 x > 0}}\) の場合
\(\large{\log_3 x > 0}\)、すなわち \(\large{x > 1}\)であるとき、(1)式の両辺に\(\large{\log_3 x}\) をかけても不等号の向きは変化しません。
$$\large{(\log_3 x)^2 -3 < 2 \log_3 x}$$ここで、\(\large{\log_3 x = X}\) (ただし、\(\large{X > 0}\)) とおくと、 $$\large{X^2 -2X -3 < 0}$$ $$\large{(X+1)(X-3) < 0 }$$ 上式を、\(\large{X >0}\) の範囲で解を求めると、\(\large{0 < X < 3}\) となります。
\(\large{\log_3 x = X}\)から、 $$\large{0 < \log_3 x < 3}$$ $$\large{\log_3 1 < \log_3 x < \log_3 3^3}$$ ここで、底が1より大きいため、対数の不等号の向きと、真数の不等号の向きが一致するため、 $$\large{1 < x < 27}$$ この解は、真数条件と底の条件\(\large{x>0,x\neq 1}\)を満たします。
【Ⅱ】\(\large{\boldsymbol{\log_3 x < 0}}\) の場合
\(\large{\log_3 x < 0}\)、すなわち \(\large{0 < x < 1}\)であるとき、(1)式の両辺に\(\large{\log_3 x}\) をかけると不等号の向きが反転します。
$$\large{(\log_3 x)^2 -3 > 2 \log_3 x}$$ここで、\(\large{\log_3 x = X}\) (ただし、\(\large{X < 0}\)) とおくと、 $$\large{X^2 -2X -3 > 0}$$ $$\large{(X+1)(X-3) > 0 }$$ 上式を、\(\large{X < 0}\) の範囲で解を求めると、\(\large{X < -1}\) となります。
\(\large{\log_3 x = X}\)から、 $$\large{\log_3 x < -1}$$ $$\large{\log_3 x < \log_3 3^{-1}}$$ ここで、底が1より大きいため、対数の不等号の向きと、真数の不等号の向きが一致するため、 $$\large{x < \frac{1}{3}}$$ ここで、真数条件と底の条件\(\large{x>0,x\neq 1}\)から、 $$\large{0 < x < \frac{1}{3}}$$ となります。
したがって、場合分けした『【Ⅰ】\(\large{\boldsymbol{\log_3 x > 0}}\) の場合』と『【Ⅱ】\(\large{\boldsymbol{\log_3 x < 0}}\) の場合』から、求める解は、 $$\large{0 < x < \frac{1}{3},\hspace{3pt}1 < x < 27}$$ となります。