四次関数と二重接線に囲まれた面積

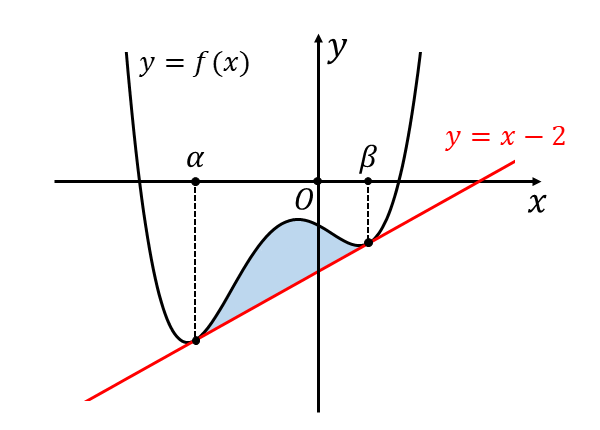
【問題(1)の答え】
　$\hspace{1pt} y = x-2\hspace{1pt}$
　

【問題(2)の答え】
　$\displaystyle S = \frac{5 \sqrt{5}}{6}\hspace{2pt}$
　

【解答のポイント】
　曲線に対して異なる$\hspace{2pt}2\hspace{1pt}$点で接する直線を二重接線(もしくは、複接線)といいます。

二次関数、三次関数には二重接線は存在しませんが、四次関数には存在することがあります。

本問は四次関数の二重接線を求め、四次関数と二重接線に囲まれた面積を求める問題です。
　

　四次関数の二重接線の求め方は以下の通りです。

　まず求める直線の方程式を$\hspace{2pt}y=ax+b\hspace{2pt}$とし、関数$\hspace{2pt}f(x)=x^4+2x^3-x^2-x-1\hspace{2pt}$との接点を$\hspace{2pt}x= \alpha , \beta\hspace{2pt}$とします。

このとき、四次方程式$\hspace{2pt}f(x) - (ax+b) = 0\hspace{2pt}$は$\hspace{2pt}x= \alpha , \beta\hspace{2pt}$において重解を持ち、かつ四次の係数が$\hspace{2pt}1\hspace{2pt}$であるので

$$\hspace{10pt}{f(x) - (ax+b) = (x-\alpha)^2 (x-\beta)^2 \hspace{10pt}}$$

と因数分解されます。

上式の左右の係数を比較することで$\hspace{2pt}a,b,\alpha,\beta\hspace{2pt}$を求めることができます。
　

【問題(1)の解答】
　問題 : 『関数$\hspace{2pt}f(x)=x^4+2x^3-x^2-x-1\hspace{2pt}$について次の問いに答えよ.
　(1) 曲線$\hspace{2pt}y = f(x)\hspace{2pt}$と異なる$\hspace{2pt}2\hspace{1pt}$点で接する直線の方程式を求めよ.
　(2) 曲線$\hspace{2pt}y = f(x)\hspace{2pt}$と問題(1)で求めた直線により囲まれる面積$\hspace{1pt}S\hspace{2pt}$を求めよ.』
　

求める直線を$\hspace{2pt}y=ax+b\hspace{2pt}$とします。

また、曲線$\hspace{2pt}y=f(x)\hspace{2pt}$と直線$\hspace{2pt}y=ax+b\hspace{2pt}$が$\hspace{2pt}x= \alpha , \beta\hspace{2pt}$$\hspace{2pt}(\alpha < \beta)\hspace{2pt}$において接するとします。

ここで、四次方程式$\hspace{2pt}f(x) - (ax+b) = 0\hspace{2pt}$は$\hspace{2pt}x= \alpha , \beta\hspace{2pt}$において重解を持ち、かつ四次の係数が$\hspace{2pt}1\hspace{2pt}$であるので

$$\hspace{10pt}{f(x) - (ax+b) = (x-\alpha)^2 (x-\beta)^2 \hspace{10pt}}$$

と因数分解されます。

上式の左辺は

$$ \begin{aligned} \hspace{10pt}& x^4+2x^3-x^2-x-1- (ax+b) \hspace{10pt} \\[0.5em] \hspace{10pt}&= x^4+2x^3-x^2-(1+a)x-1-b \hspace{10pt}\\[0.5em] \end{aligned} $$

また、右辺を展開すると

$$ \begin{aligned} \hspace{10pt} & (x-\alpha)^2 (x-\beta)^2\hspace{10pt} \\[0.5em] \hspace{10pt}&= (x^2 - 2 \alpha x + \alpha^2)(x^2 - 2 \beta x + \beta^2)\hspace{10pt}\\[0.5em] \hspace{10pt} &= x^4 -2(\alpha + \beta)x^3 + (\alpha^2 + \beta^2 +4 \alpha \beta)x^2 \hspace{10pt}\\[0.5em] \hspace{10pt} & \hspace{12pt}-2\alpha \beta(\alpha + \beta)x +\alpha^2 \beta^2 \hspace{10pt}\\[0.5em] \end{aligned} $$

となります。

左辺と右辺の係数を比較すると

$$ \begin{aligned} \hspace{10pt} 2 & = -2(\alpha + \beta) \hspace{22pt}\cdots(1)\hspace{10pt}\\[0.5em] -1 & = \alpha^2 + \beta^2 +4 \alpha \beta\hspace{3pt} \cdots(2)\\[0.5em] -(1+a) & = -2\alpha \beta(\alpha + \beta) \hspace{8pt}\cdots(3)\\[0.5em] -1-b & = \alpha^2 \beta^2 \hspace{49pt}\cdots(4)\\[0.5em] \end{aligned} $$

となります。

(1)式から $${\alpha + \beta = -1 \cdots (1')}$$ となります。

また、(2)式から $$ \begin{aligned} -1 & = \alpha^2 + \beta^2 +4 \alpha \beta\\[0.5em] & = (\alpha + \beta)^2 +2 \alpha \beta\\[0.5em] & = 1 +2 \alpha \beta\\[0.5em] -1 & = \alpha \beta \cdots (2')\\[0.5em] \end{aligned} $$ となります。

$\hspace{1pt}(1')\hspace{1pt}$と$\hspace{1pt}(2')\hspace{1pt}$より、$t= \alpha , \beta\hspace{2pt}$を解に持つ二次方程式は解と係数の関係から $${t^2 +t -1 = 0}$$ となります。

この二次方程式の解は解の公式から $${t = \frac{-1 \pm \sqrt{5}}{2}}$$ であり、$ \alpha < \beta\hspace{2pt}$より $$\alpha = \frac{-1 - \sqrt{5}}{2}\hspace{1pt} , \hspace{1pt}\beta = \frac{-1 + \sqrt{5}}{2}$$ となります。

また、(3)式より $$ \begin{aligned} -(1+a) & = -2\alpha \beta(\alpha + \beta)\\[0.5em] & = -2 \cdot(-1) \cdot (-1)\\[0.5em] & = -2\\[0.5em] a & = 1\\[0.5em] \end{aligned} $$ となります。

また、(4)式より $$ \begin{aligned} -1-b & = \alpha^2 \beta^2\\[0.5em] & = (-1)^2\\[0.5em] & = 1\\[0.5em] b & = -2\\[0.5em] \end{aligned} $$ となります。

したがって、求める直線の方程式は $${y = x-2}$$ となります。
　

【問題(2)の解答】
　問題 : 『関数$\hspace{2pt}f(x)=x^4+2x^3-x^2-x-1\hspace{2pt}$について次の問いに答えよ.
　(1) 曲線$\hspace{2pt}y = f(x)\hspace{2pt}$と異なる$\hspace{2pt}2\hspace{1pt}$点で接する直線の方程式を求めよ.
　(2) 曲線$\hspace{2pt}y = f(x)\hspace{2pt}$と問題(1)で求めた直線により囲まれる面積$\hspace{1pt}S\hspace{2pt}$を求めよ.』
　

曲線$\hspace{2pt}y = f(x)\hspace{2pt}$と異なる$\hspace{2pt}2\hspace{1pt}$点で接する直線に囲まれた面積は、以下の青く塗られた部分となります。四次関数と異なる2点で接する二重接線の図_問題

求める面積は$\displaystyle\hspace{2pt}\alpha = \frac{-1 - \sqrt{5}}{2}\hspace{1pt} , \hspace{1pt}\beta = \frac{-1 + \sqrt{5}}{2}\hspace{2pt}$とすると

$$\begin{aligned} \hspace{15pt} S = & \int_{\alpha}^\beta \left \{ x^4+2x^3-x^2-x-1- (x-2)\right \} \hspace{1pt}dx \hspace{10pt}\\[1.2em] \hspace{10pt} = & \int_{\alpha}^\beta (x-\alpha)^2 (x-\beta)^2 \hspace{1pt}dx \hspace{10pt}\\[1.2em] \hspace{10pt} = & \int_{\alpha}^\beta (x-\alpha)^2 \{ (x - \alpha) - (\beta-\alpha) \}^2 \hspace{1pt}dx \hspace{10pt}\\[1.2em] \hspace{10pt} = & \int_{\alpha}^\beta (x-\alpha)^2 \{ (x - \alpha)^2 -2(\beta-\alpha)(x - \alpha) + (\beta-\alpha)^2 \} \hspace{1pt}dx \hspace{10pt}\\[1.2em] \hspace{10pt} = & \int_{\alpha}^\beta \{ (x-\alpha)^4 -2(\beta-\alpha)(x - \alpha)^3 + (\beta-\alpha)^2(x-\alpha)^2 \} \hspace{1pt}dx \hspace{10pt}\\[1.2em] \hspace{10pt} =& \left [ \frac{1}{5}(x-\alpha)^5 -2(\beta-\alpha) \cdot \frac{1}{4}(x - \alpha)^4 +(\beta-\alpha)^2 \cdot \frac{1}{3}(x - \alpha)^3\right ]_{\alpha}^\beta\hspace{20pt}\\[1.2em] \hspace{10pt} =& \frac{1}{30}(\beta - \alpha)^5\hspace{10pt}\\[1.2em] \hspace{10pt} =& \frac{1}{30} \left(\frac{-1 + \sqrt{5}}{2} - \frac{-1 - \sqrt{5}}{2} \right)^5\hspace{10pt}\\[1.2em] \hspace{10pt} =& \frac{5 \sqrt{5}}{6}\hspace{10pt}\\[1.2em] \end{aligned} $$

と求められます。
　

【入試本番に向けたアドバイス】
　本問は四次関数の二重接線を求め、四次関数と二重接線に囲まれた面積を求める問題です。

本問のように、四次関数の曲線と二重接線で囲まれた面積には、以下の1/30公式が成り立つことが知られています。

　異なる$\hspace{2pt}2\hspace{2pt}$点$\hspace{2pt}x = \alpha , \beta\hspace{2pt}$$\hspace{2pt}(\beta > \alpha )\hspace{2pt}$を接点に持つ二重接線と四次関数$\hspace{2pt}y = a(x-\alpha)^2(x-\beta)^2\hspace{2pt}$に囲まれた面積$\hspace{2pt}S\hspace{2pt}$は $${S = \frac{|a|}{30}(\beta - \alpha)^5}$$ と求められる。

1/30公式は入試問題では活用の機会が少なく覚える必要はありませんが、必要なときに導出ができるように計算の練習をしておきましょう。

　本問の面積を求める計算の途中では、以下のように被積分関数を変形して計算を行いました。

$$\begin{aligned} \hspace{20pt} & \int_{\alpha}^\beta (x-\alpha)^2 (x-\beta)^2 \hspace{1pt}dx \hspace{10pt}\\[1.2em] \hspace{10pt} = & \int_{\alpha}^\beta (x-\alpha)^2 \{ (x - \alpha) - (\beta-\alpha) \}^2 \hspace{1pt}dx \hspace{10pt}\\[1.2em] \hspace{10pt} = & \int_{\alpha}^\beta (x-\alpha)^2 \{ (x - \alpha)^2 -2(\beta-\alpha)(x - \alpha) + (\beta-\alpha)^2 \} \hspace{1pt}dx \hspace{20pt}\\[1.2em] \hspace{10pt} = & \int_{\alpha}^\beta \{ (x-\alpha)^4 -2(\beta-\alpha)(x - \alpha)^3 + (\beta-\alpha)^2(x-\alpha)^2 \} \hspace{1pt}dx \hspace{20pt}\\[1.2em] \end{aligned} $$

このように式変形すると $${\int (x-\alpha)^4 dx = \frac{1}{5}(x-\alpha)^5+C}$$ など簡単な積分の和になるため、式展開する手間を省けるので計算時間を短縮できます。
　

【関連するページ】
・定積分
　