3つの曲線に囲まれた面積を求める問題

【答え】
　$\displaystyle\hspace{3pt}\frac{\pi}{2} - \frac{5\sqrt{5}}{32}$
　

【解答のポイント】
$x^2 + y^2 \leqq 1\hspace{2pt}$は円の内部を表す不等式です。
このような円を含む領域の面積を考えるときは、半径$\hspace{1pt}r\hspace{1pt}$の円の面積$\hspace{2pt}\pi r^2\hspace{2pt}$を利用します。

また、$y \geqq f(x) \hspace{1pt}, \hspace{1pt}y \geqq g(x) \hspace{2pt}$は2つの三次関数のグラフのうち、上側にある領域を表します
　

定積分の計算では$\hspace{2pt}y = f(x) \hspace{2pt}$と$\hspace{2pt}y = g(x) \hspace{2pt}$の交点の座標を用いますが、交点がルートを含む複雑な形となり計算に時間がかかります。

そこで、一旦交点の$\hspace{2pt}x\hspace{1pt}$座標を$\hspace{2pt}x = \alpha , \beta\hspace{2pt}$とおき、後から解と係数の関係を利用して$\hspace{1pt}\beta - \alpha\hspace{1pt}$を計算すると、定積分を簡単に求められます。
　

【問題(1)の解答】
　問題 : 次の問いに答えよ.
　(1) 関数$\hspace{1pt}f(x)\hspace{2pt}$を$\hspace{2pt}f(x) = x^3-x\hspace{2pt}$とする. 曲線$\hspace{2pt}y=f(x)\hspace{2pt}$のグラフの概形を描け.
　(2) 曲線$\hspace{2pt}y=f(x)\hspace{2pt}$を$\hspace{2pt}x\hspace{1pt}$軸方向に$\displaystyle\hspace{2pt}\frac{1}{2}\hspace{2pt}$だけ平行移動した曲線を$\hspace{2pt}y=g(x)\hspace{2pt}$とする. 次の連立不等式を満たす部分の面積$\hspace{1pt}S\hspace{2pt}$を求めよ.
$$ \begin{dcases} & x^2 + y^2 \leqq 1 \\[0.5em] & y \geqq f(x)\\[0.5em] & y \geqq g(x)\\ \end{dcases} $$
　

$\displaystyle {f(x)=x^3-x}$ を微分すると $${f'(x)=3x^2-1}$$ となります。

${f'(x)=0}$ を解くと $$\begin{aligned} 3x^2-1 & =0\\[0.5em] x^2 & =\frac{1}{3}\\[0.5em] x & = \pm\frac{\sqrt{3}}{3}\\[0.5em] \end{aligned}$$ となります。

ここで、$\displaystyle{x=\pm \frac{\sqrt{3}}{3}}$ の前後における $\displaystyle{f'(x)}$ の符号の変化を調べます。

${f'(x)=3x^2-1 }$ より
　$\displaystyle{x < -\frac{\sqrt{3}}{3}}$ 　　　のとき ${f'(x)>0}$
　$\displaystyle{-\frac{\sqrt{3}}{3} < x < \frac{\sqrt{3}}{3}\hspace{2pt}}$ のとき ${f'(x)< 0}$
　$\displaystyle{ x > \frac{\sqrt{3}}{3}}$ 　　　　のとき ${f'(x) > 0}$
となります。

よって、関数$\displaystyle {f(x)}$ は$\displaystyle{\hspace{2pt}x=-\frac{\sqrt{3}}{3}}$ で極大値、$\displaystyle{x=\frac{\sqrt{3}}{3}}$ で極小値をとります。

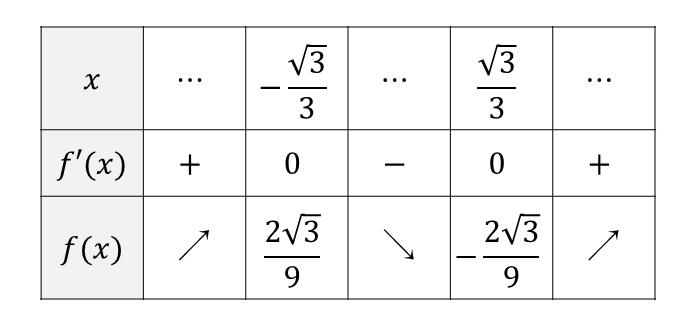
以上から、増減表を作成すると以下のようになります。 f(x)=x^3-xの増減表
　

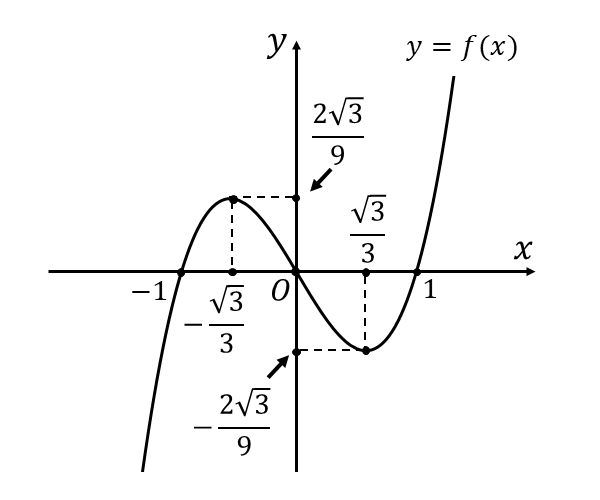
この増減表からグラフを描くと、以下のようになります。 f(x)=x^3-xのグラフ
　

【問題(2)の解答】
　問題 : 次の問いに答えよ.
　(1) 関数$\hspace{1pt}f(x)\hspace{2pt}$を$\hspace{2pt}f(x) = x^3-x\hspace{2pt}$とする. 曲線$\hspace{2pt}y=f(x)\hspace{2pt}$のグラフの概形を描け.
　(2) 曲線$\hspace{2pt}y=f(x)\hspace{2pt}$を$\hspace{2pt}x\hspace{1pt}$軸方向に$\displaystyle\hspace{2pt}\frac{1}{2}\hspace{2pt}$だけ平行移動した曲線を$\hspace{2pt}y=g(x)\hspace{2pt}$とする. 次の連立不等式を満たす部分の面積$\hspace{1pt}S\hspace{2pt}$を求めよ.
$$ \begin{dcases} & x^2 + y^2 \leqq 1 \\[0.5em] & y \geqq f(x)\\[0.5em] & y \geqq g(x)\\ \end{dcases} $$
　

曲線$\hspace{2pt}y=g(x)\hspace{2pt}$を求めると、$\displaystyle {f(x)=x^3-x}$ を$\hspace{2pt}x\hspace{1pt}$軸方向に$\displaystyle\hspace{2pt}\frac{1}{2}\hspace{2pt}$だけ平行移動すればよいので $$ \begin{aligned} g(x) & = f(x - \frac{1}{2}) \\[1.2em] &= \left(x-\frac{1}{2}\right)^3 - \left(x-\frac{1}{2}\right) \\[1.2em] &= x^3-\frac{3}{2}x^2-\frac{x}{4} + \frac{3}{8}\\[1.2em] \end{aligned} $$ となります。

ここで、$f(x)=g(x)\hspace{2pt}$を解くと

$$\begin{aligned} \hspace{10pt} x^3 -x & = x^3-\frac{3}{2}x^2-\frac{x}{4} + \frac{3}{8}\hspace{10pt}\\[1.2em] & \frac{3}{2}x^2 - \frac{3}{4}x - \frac{3}{8}= 0 \\[1.2em] & 4x^2 -2x -1= 0 \cdots (1)\\[1.2em] \end{aligned} $$

(1)式の解を$\hspace{2pt}\alpha ,\beta\hspace{2pt}$(ただし、$\alpha < \beta \hspace{2pt}$)とすると、解と係数の関係から $${\alpha + \beta = \frac{1}{2}\hspace{1pt},\hspace{1pt} \alpha \beta = -\frac{1}{4}}$$ となります。

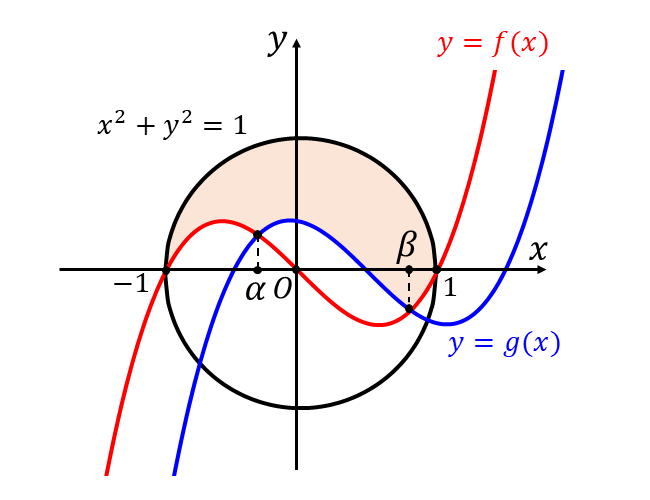
問題(1)のグラフから連立不等式を満たす部分を図示すると、以下のオレンジ色に塗られた領域となります。連立不等式の示す領域
　

図より、求める面積$\hspace{1pt}S\hspace{2pt}$は

$$\begin{aligned} \hspace{10pt} S = & \frac{\pi}{2} + \int_0^1 -f(x) \hspace{1pt}dx \hspace{10pt}\\[1.2em] & - \int_{-1}^0 f(x) \hspace{1pt}dx -\int_\alpha^\beta \{g(x) - f(x)\} \hspace{1pt}dx \hspace{10pt}\\ \end{aligned} $$

となります。
(式中の$\displaystyle\hspace{2pt}\frac{\pi}{2} \hspace{2pt}$は半径$\hspace{1pt}1\hspace{1pt}$の円の上半分の面積を表しています。)

$\displaystyle\hspace{2pt} \int_0^1 -f(x) \hspace{1pt}dx - \int_{-1}^0 f(x) \hspace{1pt}dx\hspace{2pt}$を求めると

$$\begin{aligned} \hspace{10pt} & \int_0^1 -f(x) \hspace{1pt}dx - \int_{-1}^0 f(x) \hspace{1pt}dx \hspace{10pt}\\[1.2em] \hspace{10pt} &= - \left\{\int_0^1 f(x) \hspace{1pt}dx + \int_{-1}^0 f(x) \hspace{1pt}dx\right \}\hspace{10pt}\\[1.2em] \hspace{10pt} &= - \int_{-1}^1 f(x) \hspace{1pt}dx \hspace{10pt}\\[1.2em] \hspace{10pt} &= - \int_{-1}^1 (x^3-x) \hspace{1pt}dx \hspace{10pt}\\[1.2em] & = 0\\[1.2em] \end{aligned} $$

となります。
(上記の計算には$\hspace{2pt}f(x)=x^3-x\hspace{2pt}$が奇関数であることから、$\int_{-1}^1 f(x) \hspace{1pt}dx=0\hspace{2pt}$であることを用いています。)
　

次に$\displaystyle\hspace{2pt} \int_\alpha^\beta \{g(x) - f(x)\} \hspace{1pt}dx \hspace{2pt}$を求めます。

$$\begin{aligned} \hspace{10pt} & \int_\alpha^\beta \{g(x) - f(x)\} \hspace{1pt}dx\hspace{10pt}\\[1.2em] & = \int_\alpha^\beta \frac{3}{2}(x-\alpha)(x - \beta) \hspace{1pt}dx \\[1.2em] & = -\frac{3}{2} \left\{-\frac{1}{6}(\beta - \alpha)^3\right\} \\[1.2em] & = \frac{1}{4}(\beta - \alpha)^3 \\[1.2em] \end{aligned} $$

(上記の計算には1/6公式 $$ \begin{aligned} & \int_\alpha^{\beta}(x-\alpha)(x-\beta)\hspace{1pt}dx \\[0.7em] &= -\frac{1}{6}(\beta - \alpha)^3 \\[0.7em] \end{aligned} $$ を用いています。)
　

ここで、先に求めた $${\alpha + \beta = \frac{1}{2}\hspace{1pt},\hspace{1pt} \alpha \beta = -\frac{1}{4}}$$ を利用し、$\beta - \alpha\hspace{2pt}$の値を求めます。 $$ \begin{aligned} (\beta - \alpha)^2 &= \alpha^2 - 2\alpha\beta + \beta^2 \\[0.7em] &= (\alpha + \beta)^2 -4 \alpha\beta\\[0.7em] &= \frac{1}{4} - 4 \cdot \left ( -\frac{1}{4}\right)\\[0.7em] &= \frac{1}{4} +1\\[0.7em] &=\frac{5}{4}\\[0.7em] \end{aligned} $$ ここで、$\beta - \alpha > 0\hspace{2pt}$であるので $${\beta - \alpha = \frac{\sqrt{5}}{2}}$$ となります。

よって $$ \begin{aligned} & \int_\alpha^\beta \{g(x) - f(x)\} \hspace{1pt}dx \\[1em] &= \frac{1}{4}(\beta - \alpha)^3 \\[1em] &= \frac{1}{4}\left(\frac{\sqrt{5}}{2}\right)^3\\[1.2em] &= \frac{1}{4} \cdot \frac{5\sqrt{5}}{8}\\[1.2em] &= \frac{5\sqrt{5}}{32}\\[0.7em] \end{aligned} $$

となります。
　

したがって、求める面積は

$$ \begin{aligned} \hspace{10pt} S = & \frac{\pi}{2} + \int_0^1 -f(x) \hspace{1pt}dx \hspace{10pt}\\[1.2em] & - \int_{-1}^0 f(x) \hspace{1pt}dx -\int_\alpha^\beta \{g(x) - f(x)\} \hspace{1pt}dx \hspace{10pt} \\[1.2em] = & \frac{\pi}{2} - \frac{5\sqrt{5}}{32} \hspace{10pt}\\ \end{aligned} $$

と求められます。
　

【入試本番に向けたアドバイス】
　本問は、円と2つの三次関数に囲まれた部分の面積を求める問題です。

数学Ⅱの定積分の分野において『円に囲まれた部分の面積を求める問題』はよく出題されるパターンの1つです。

本問のように、『円の内部が二次関数や三次関数に切り取られている面積』は、半径$\hspace{1pt}r\hspace{1pt}$の円の面積$\hspace{2pt}\pi r^2 \hspace{2pt}$から切り取られた面積を足し引きして解ける場合が多いです。
　

また、類題として『円の一部(扇形)と二次関数や三次関数に囲まれた面積の和』もよく出題されるパターンの1つです。

この場合は、求める面積を『半径$\hspace{1pt}r\hspace{1pt},\hspace{1pt}$中心角$\hspace{1pt}a^\circ\hspace{1pt}$の扇形の面積$\hspace{2pt}\pi r^2 \times \frac{a}{360}\hspace{2pt}$』と『二次関数や三次関数に囲まれた部分』に分割すると計算できることが多いです。
(この問題は円と二次関数に囲まれた面積で取り上げています。)
　

求める面積に円が含まれている場合は、まず『円の面積$\hspace{2pt}\pi r^2 \hspace{2pt}$』や『扇形の面積$\hspace{2pt}\pi r^2 \times \frac{a}{360}\hspace{2pt}$』が利用できないかを考えるようにしましょう。
　

【関連するページ】
・定積分

・1/6公式
　