円と二次関数に囲まれた内部の面積

【答え】
　\(\displaystyle { \frac{\sqrt{3} +2\pi }{12}}\)
　

【解答のポイント】
\(x^2 + y^2 = 1\hspace{2pt}\)を\(\hspace{2pt}x \geqq 0\hspace{2pt}\)の範囲で\(\hspace{2pt}y\hspace{2pt}\)について解くと $${y = \sqrt{1 - x^2}}$$ となり、この定積分は数学Ⅱの範囲では求めることができません。

そこで、求める面積を『扇形』と『直線と二次関数に囲まれた部分』に分割すると、定積分の計算を省くことができます。

扇形の面積\(\hspace{1pt}S\hspace{1pt}\)は半径\(\hspace{1pt}r\hspace{1pt}\)、中心角が\(\hspace{1pt}a^\circ\hspace{1pt}\)であるとき $${S = \pi r^2 \times \frac{a}{360}}$$ から求められます。
　

【解答】
　問題 : 次の連立不等式を満たす部分の面積を求めよ
$$ \begin{dcases} & x^2 + y^2 \leqq 1 \\[0.7em] & y \geqq 2 \sqrt{3} x^2 \end{dcases} $$
　

まず、\(y^2 + x^2 = 1\hspace{2pt}\)と\(\hspace{2pt}y = 2 \sqrt{3}x^2\hspace{2pt}\)の交点の座標を求めます。

\(\hspace{1pt}2\hspace{1pt}\)式を連立させ、交点の\(y\hspace{1pt}\)座標を求めると $$ \begin{aligned} \hspace{10pt} y^2 + x^2 = & 1\\[0.7em] y^2 + \frac{y}{ 2 \sqrt{3}} = & 1 \\[1em] 2 \sqrt{3}y^2 + y - 2 \sqrt{3}= & 0 \\[1em] (2y - \sqrt{3}) (\sqrt{3} y + 2)= & 0 \\[1em] \end{aligned} $$

ここで、\(y \geqq 0\hspace{2pt}\)であることから、\(\displaystyle y = \frac{\sqrt{3}}{2}\hspace{2pt}\)となります。

また、交点の\(x\hspace{1pt}\)座標は $$ \begin{aligned} \hspace{10pt} \left(\frac{\sqrt{3}}{2} \right)^2 + x^2 = & 1\\[1em] x^2 = & \frac{1}{4} \\[1em] \end{aligned} $$

つまり、\(\displaystyle x =\pm \frac{1}{2}\hspace{2pt}\)となります。

したがって、交点の座標は $${(x,y) = \left(\pm \frac{1}{2} \hspace{1pt},\hspace{1pt} \frac{\sqrt{3}}{2} \right)}$$ となります。

ここで、\(x^2 + y^2 \leqq 1 \hspace{2pt}\)と\(\hspace{2pt}y \geqq 2 \sqrt{3} x^2 \hspace{2pt}\)の満たす部分を図示すると以下の青色の部分となります。

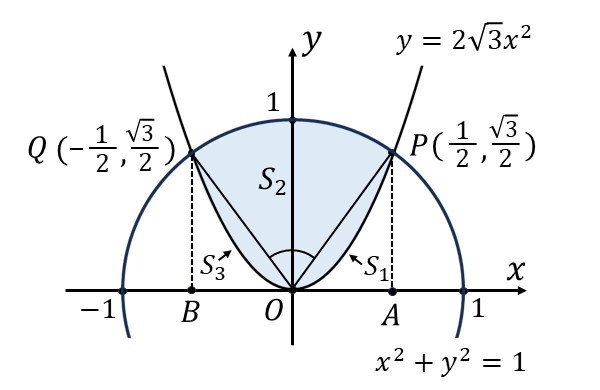
上図において、\(y^2 + x^2 = 1\hspace{2pt}\)と\(\hspace{2pt}y = 2 \sqrt{3}x^2\hspace{2pt}\)の交点を\(\hspace{1pt}P, Q\hspace{1pt}\)とし、その交点から\(\hspace{1pt}x\hspace{1pt}\)軸に下した垂線の足を点\(\hspace{1pt}A , B\hspace{1pt}\)とします。

ここで、上図の面積を『直線と二次関数に囲まれた面積\({S_1,\hspace{1pt}S_3 \hspace{2pt}}\)』と『扇形\({S_2 \hspace{2pt}}\)』の\(\hspace{1pt}3\hspace{1pt}\)つの部分に分けて考えます。
　

・面積\(\hspace{1pt}S_1\hspace{1pt}\)の求め方
　まず、面積\({S_1\hspace{2pt}}\)は直線\(\hspace{2pt}y = \sqrt{3}x\hspace{2pt}\)と二次関数\(\hspace{2pt}y = 2 \sqrt{3} x^2\hspace{2pt}\)に囲まれた面積となります。

つまり、面積\(\hspace{1pt}S_1 \hspace{1pt}\)は $$ \begin{aligned} \hspace{10pt}S_1 = & \int_0^{\frac{1}{2}} \left(\sqrt{3}x - 2 \sqrt{3} x^2\right)dx\\[1em] = & \left[ \frac{\sqrt{3}}{2}x^2 - \frac{2\sqrt{3}}{3}x^3 \right]_0^{\frac{1}{2}} \\[1em] = & \frac{\sqrt{3}}{2}\cdot \frac{1}{4} - \frac{2\sqrt{3}}{3}\cdot \frac{1}{8} \\[1em] = & \frac{3\sqrt{3}}{24} - \frac{2\sqrt{3}}{24} \\[1em] = & \frac{\sqrt{3}}{24} \\[1em] \end{aligned} $$ と求められます。
　

・面積\(\hspace{1pt}S_3\hspace{1pt}\)の求め方
　また、面積\(\hspace{1pt}S_3\hspace{1pt}\)は\(\hspace{1pt}S_1\hspace{1pt}\)と同様に $$ \begin{aligned} \hspace{10pt}S_3 = & \int_{-\frac{1}{2}}^{0} \left(-\sqrt{3}x - 2 \sqrt{3} x^2\right)dx\\[1em] = & \frac{\sqrt{3}}{24} \\[1em] \end{aligned} $$ と求められます。
　

・面積\(\hspace{1pt}S_2\hspace{1pt}\)の求め方
　次に、扇形の面積\(\hspace{1pt}S_2\hspace{1pt}\)を求めます。

直角三角形\(\hspace{1pt}OAP\hspace{1pt}\)において、辺\(\hspace{1pt}OA\hspace{1pt}\)と辺\(\hspace{1pt}PA\hspace{1pt}\)の比が\(\hspace{1pt}1 : \sqrt{3}\hspace{1pt}\)であることから、\(\angle P \hspace{1pt} OA\hspace{1pt}\)は\(\hspace{1pt}60 ^\circ\hspace{1pt}\)となります。
同様に、\(\angle Q \hspace{1pt} OB\hspace{1pt}\)も\(\hspace{1pt}60 ^\circ\hspace{1pt}\)となります。

したがって、扇形の中心角である\(\hspace{1pt}\angle P \hspace{1pt} OQ\hspace{1pt}\)は\(\hspace{1pt}60 ^\circ\hspace{1pt}\)となります。

以上から、面積\({\hspace{1pt}S_2\hspace{2pt}}\)は半径\({1\hspace{1pt}}\), 中心角\({\hspace{1pt} 60°\hspace{2pt}}\)の扇形の面積であるため $$ \begin{aligned} \hspace{10pt}S_2 = & \pi \times 1^2 \times \frac{60}{360}\\[0.5em] = & \frac{\pi}{6} \\ \end{aligned} $$ となります。

すなわち、求める面積は $$ \begin{aligned} \hspace{10pt}& S_1 + S_2 + S_3 \\[0.5em] & = \frac{\sqrt{3}}{24} + \frac{\pi}{6} + \frac{\sqrt{3}}{24}\\[0.7em] & = \frac{\sqrt{3} +2\pi }{12}\\[1em] \end{aligned} $$ となります。
　

【入試本番に向けたアドバイス】
本問は、求める面積を『扇形』と『直線と二次関数に囲まれた部分』に分割することで、難しい定積分の計算を省くことがポイントになります。

一見すると定積分の問題であっても、定積分を計算せずに済む方法はないかを常に考えることが重要です。

例えば、本問の類題として定積分\(\displaystyle\hspace{1pt}\int_{-a}^a \sqrt{a^2-x^2} \hspace{1pt} dx\hspace{1pt}\)\(\hspace{1pt}(a>0)\hspace{1pt}\)は、\(\displaystyle y = \sqrt{a^2 - x^2}\hspace{1pt}\)が半径\({a\hspace{2pt}}\)の円の上半分を表すことから $${\int_{-a}^a \sqrt{a^2-x^2} \hspace{1pt} dx = \frac{\pi}{2}a^2}$$ とすぐに求めることができます。
　

【関連するページ】
・定積分

・円の面積を求める積分