p+q,pqの存在する範囲の面積を求める問題

【答え】
　$\displaystyle\hspace{3pt}\frac{2\sqrt{2}}{3}$
　

【解答のポイント】
まず、条件式$\hspace{2pt}p^2+q^2 \leqq 1\hspace{2pt}$を $${(p+q)^2 -2 pq \leqq 1}$$ と変形し、$x,y\hspace{2pt}$の式に変形します。
　

また、上記の条件式とは別に実数$\hspace{2pt}p , q\hspace{2pt}$が存在する範囲も考える必要があります。

例えば$\hspace{3pt}(x,y) = (1,1)\hspace{2pt}$という値に対しては $${p + q = 1 \hspace{1pt}, \hspace{1pt}pq = 1}$$ を満たす$\hspace{2pt}p , q\hspace{2pt}$が実数の範囲で存在しないことから、$(x,y) = (1,1)\hspace{2pt}$は存在する範囲から除外する必要があります。

そこで、$(x,y)\hspace{2pt}$に対して $${p + q = x \hspace{1pt}, \hspace{1pt}pq = y}$$ を満たす$\hspace{2pt}p , q\hspace{2pt}$が実数の範囲に存在するために、解と係数の関係を用いて$\hspace{2pt}t = p ,q\hspace{2pt}$が解となる二次方程式 $${t^2-x t + y = 0}$$ が実数解を持つ、すなわち上記の二次方程式の判別式が$\hspace{2pt}D \geqq 0\hspace{2pt}$であるという条件を加えます。
　

【問題の解答】
　問題 : 『実数$\hspace{2pt}p,q\hspace{2pt}$が$\hspace{2pt}p^2+q^2 \leqq 1\hspace{2pt}$を満たしながら動くとする.
　$x = p+q \hspace{1pt},\hspace{1pt} y=pq\hspace{2pt}$とするとき, 点$\hspace{2pt}(x,y)\hspace{2pt}$の存在する面積を求めよ.』
　

条件式$\hspace{2pt}p^2+q^2 \leqq 1\hspace{2pt}$を変形すると $${(p+q)^2 -2 pq \leqq 1}$$ となります。

$x = p+q \hspace{1pt},\hspace{1pt} y=pq\hspace{2pt}$を代入すると $${x^2 -2 y \leqq 1}$$ すなわち $${y \geqq \frac{1}{2}x^2 - \frac{1}{2} \cdots (1)}$$ となります。
　

ここで、実数$\hspace{2pt}p,q\hspace{2pt}$が存在する範囲を求めます。

解と係数の関係から$\displaystyle\hspace{2pt} p + q =x\hspace{2pt},$$\displaystyle\hspace{2pt}p q = y\hspace{2pt}$であることを用いると、二次方程式 $$ t^2-xt+y = 0 $$ の判別式が$\hspace{2pt}D \geqq 0\hspace{2pt}$であればよいので $${x^2 -4 y \geqq 0}$$ すなわち $${ y \leqq \frac{1}{4}x^2 \cdots (2)}$$ が実数$\hspace{2pt}p,q\hspace{2pt}$が存在する範囲となります。

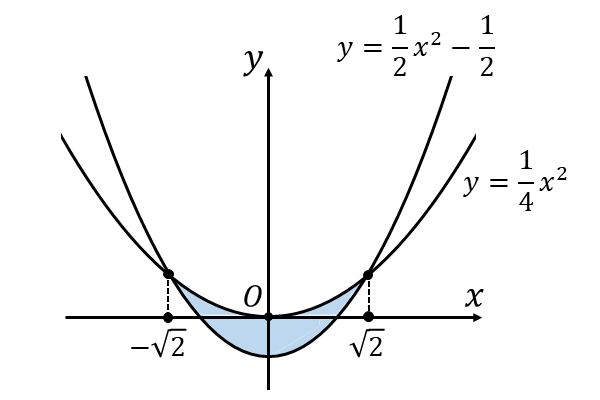
したがって、(1)式と(2)式の範囲を図示すると、以下の青く塗られた領域(ただし、境界線を含む)となります。 p+q,pqの存在する範囲の面積
　

したがって、求める面積は

$$ \begin{aligned} \hspace{10pt} & \int_{-\sqrt{2}}^{\sqrt{2}} \left \{\frac{1}{4}x^2 - \left(\frac{1}{2}x^2 - \frac{1}{2} \right) \right \}\hspace{1pt}dx \\[1.2em] &= - \int_{-\sqrt{2}}^{\sqrt{2}} \left (\frac{1}{4}x^2 - \frac{1}{2} \right )\hspace{1pt}dx \\[1.2em] &= - \frac{1}{4}\int_{-\sqrt{2}}^{\sqrt{2}} \left (x^2 - 2 \right )\hspace{1pt}dx \\[1.2em] &= - \frac{1}{4}\int_{-\sqrt{2}}^{\sqrt{2}} (x+\sqrt{2})(x-\sqrt{2})\hspace{1pt}dx \\[1.2em] &= - \frac{1}{4} \cdot \left \{ - \frac{(\sqrt{2} - (-\sqrt{2}))^3}{6} \right \} \\[1.2em] &= \frac{2\sqrt{2}}{3} \\[0.7em] \end{aligned} $$

と求められます。

(上記の計算には1/6公式 $$ \begin{aligned} & \int_\alpha^{\beta}(x-\alpha)(x-\beta)\hspace{1pt}dx \\[0.7em] &= -\frac{1}{6}(\beta - \alpha)^3 \\[0.7em] \end{aligned} $$ を用いています。)
　

【入試本番に向けたアドバイス】
　本問は、$\hspace{2pt}p , q\hspace{2pt}$が実数の範囲に存在するために、解と係数の関係を用いて$\hspace{2pt} p ,q\hspace{2pt}$が解となる二次方程式 $${t^2-x t + y = 0}$$ が実数解を持つ、すなわち判別式が$\hspace{2pt}D \geqq 0\hspace{2pt}$であるという条件を用いました。

このような$\hspace{2pt}p , q\hspace{2pt}$が実数の範囲に存在する条件のことを実数条件といいます。

積分の問題に限らず$\hspace{2pt}x = p + q \hspace{1pt},\hspace{1pt} y = pq\hspace{2pt}$などと置き換えをする問題は$\hspace{3pt}p , q\hspace{2pt}$が実数となる条件を確認する必要があります。

問題文に『$\hspace{2pt}p , q\hspace{2pt}$が実数である』という言葉があってもつい忘れてしまいがちですが、変数を置き換える問題では必ず意識しておきましょう。
　

【関連するページ】
・定積分

・1/6公式
　