放物線と2つの接線に囲まれた面積の最小値

【答え】
　\(\displaystyle{\frac{4\sqrt{2}}{3}}\)
　

【解答のポイント】
与えられた条件から交点の\({\hspace{1pt}x\hspace{2pt}}\)座標を求めて定積分を計算しようとすると、計算が煩雑になります。

そこで、曲線 \({y=ax^2+bx+c}\) と 2本の接線との接点の\({\hspace{1pt}x}\)座標を \({x=\alpha,\hspace{2pt}\beta}\) としたとき囲まれる面積\({\hspace{1pt}S\hspace{2pt}}\)を求める1/12公式
$$\displaystyle{S = \frac{|a|}{12}(\beta-\alpha)^3}$$ から『\({\hspace{1pt}(\beta - \alpha)\hspace{2pt}}\)が最小値』 のとき 『面積\({\hspace{1pt}S\hspace{2pt}}\)が最小値』となることを利用します。
　

【解答】
　問題 : 『曲線 \({\hspace{2pt}y=x^2}\) を \({C}\) とする。直線 \({y=2x-3}\) 上を動く点から引いた\({2\hspace{1pt}}\)本の接線 と 曲線 \({C}\) によって囲まれる面積 \({S}\) が最小になるときの面積を求めよ』

直線 \({y=2x-3}\) 上を動く点の座標を \({(\hspace{1pt}p\hspace{1pt},\hspace{1pt}2p-3\hspace{1pt})}\) とします。

曲線 \({y=x^2}\) と 座標\({(\hspace{1pt}p\hspace{1pt},\hspace{1pt}2p-3\hspace{1pt})}\) から曲線\({\hspace{1pt}C\hspace{2pt}}\)に引かれた\({\hspace{1pt}2\hspace{1pt}}\)本の接線 に囲まれた面積\({\hspace{1pt}S\hspace{2pt}}\)を図示すると、以下のようになります。

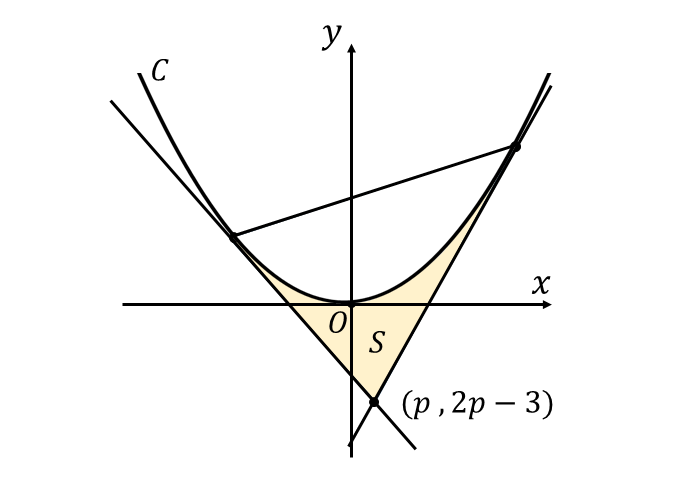
また、曲線 \({\hspace{2pt}y=x^2}\) 上の接点\({(t,t^2)}\) における接線の方程式は $${y - t^2 = 2t(x-t)}$$ すなわち $$ \begin{aligned} y & = 2t(x-t) + t^2 \\[0.5em] &= 2tx - t^2\\[0.5em] \end{aligned} $$ となります。

この接線が 点\({(p,2p-3)}\) を通るとすると $${2p-3 = 2t\cdot p - t^2}$$ 式を整理すると $${t^2 -2p\hspace{1pt}t +2p-3 = 0\cdots(1)}$$ となります。この\({\hspace{1pt}t\hspace{3pt}}\)の二次方程式の解が 曲線と接線の交点の\({\hspace{2pt}x\hspace{1pt}}\)座標 となります。

(1)式の判別式を計算すると $$ \begin{aligned} \frac{D}{4} & = (-p)^2 - (2p-3) \\[0.5em] &= p^2-2p+3\\[0.5em] &= (p-1)^2 +2\\[0.5em] \end{aligned} $$ と変形されます。

したがって、常に\({D > 0 }\)となるため、すべての\({\hspace{1pt}p\hspace{2pt}}\)に対して\({\hspace{1pt}2\hspace{1pt}}\)つの異なる交点を持ちます。

曲線\({\hspace{1pt}C\hspace{1pt}}\)と接線の交点の\({\hspace{1pt}x\hspace{1pt}}\)座標を \({x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\)\(\hspace{1pt}(\alpha < \beta)\hspace{1pt}\)とすると、1/12公式から面積\({\hspace{1pt}S\hspace{2pt}}\)は以下のようになります。 $$ \begin{aligned} S & = \frac{|a|}{12}(\beta - \alpha)^3\\[0.7em] &= \frac{1}{12}(\beta - \alpha)^3\\[0.5em] \end{aligned} $$

ここで、解の公式から (1)式 \({t^2 -2pt +2p-3 = 0}\) を解き、接線の交点の\({\hspace{1pt}x\hspace{2pt}}\)座標の差分\({\hspace{2pt}\beta-\alpha}\) を求めると以下のようになります。

よって、\({p=1}\) のとき \({\beta - \alpha}\) は最小値 \({2\sqrt{2}}\) となります。

求める面積が\({\displaystyle\hspace{1pt}S = \frac{1}{12}(\beta - \alpha)^3\hspace{2pt}}\)であることから、\({\beta - \alpha = 2\sqrt{2}\hspace{2pt}}\)のときに最小値となります。

したがって、求める面積の最小値\(\hspace{1pt}S\hspace{1pt}\)は $$ \begin{aligned} S & = \frac{1}{12}(2\sqrt{2})^3\\[0.5em] &=\frac{4\sqrt{2}}{3}\\[0.5em] \end{aligned} $$ となります。

以上から、\({p=1 \hspace{2pt}}\)すなわち点\({(\hspace{1pt}1\hspace{1pt},\hspace{2pt}-1\hspace{1pt})}\) から接線を引いたときに 面積が最小値 \(\displaystyle{\frac{4\sqrt{2}}{3}}\) となります。
　

【入試本番に向けたアドバイス】
　本問は、二次関数と\(\hspace{1pt}2\hspace{1pt}\)本の接線に囲まれた部分の面積を求める問題です。

本問では
　(1) 接線の方程式が満たす二次方程式の判別式\(\hspace{1pt}D\hspace{1pt}\)を求める
　(2) 接点の\(\hspace{1pt}x\hspace{1pt}\)座標を\(\hspace{1pt}\alpha \hspace{1pt}, \hspace{1pt}\beta\hspace{1pt}\)\(\hspace{1pt}(\alpha < \beta)\hspace{1pt}\)として1/12公式から面積を求める
　(3) \(\hspace{1pt}\beta - \alpha\hspace{2pt}\)の最小値から、面積の最小値を求める
という流れで面積を求めます。

文字を含む二次方程式を解き、交点の\(\hspace{1pt}x\hspace{1pt}\)座標を求めて定積分を計算しようとすると、定積分の計算が煩雑になる場合が多いです。

そこで、上記の(1)～(3)のように 二次方程式の解を\(\hspace{1pt}x =\alpha \hspace{1pt}, \hspace{1pt}\beta\hspace{1pt}\)\(\hspace{1pt}(\alpha < \beta)\hspace{1pt}\)とし、\(\beta- \alpha\hspace{2pt}\)の最小値を先に求めます。

求める面積が\({\displaystyle\hspace{1pt}S = \frac{1}{12}(\beta - \alpha)^3\hspace{2pt}}\)であることから、簡単に面積の最小値を求めることができます。

上記の計算の流れは、他の直線と二次関数で囲まれた面積の最小値を求める問題でも有効なため、覚えておくと計算時間の短縮や検算に便利なテクニックとなります。
　

【関連するページ】
・定積分

・1/12公式