直交する円柱の共通部分の体積を求める問題と解き方

【問題(1)の答え】
　$\displaystyle \frac{16}{3}a^3 $

【問題(2)の答え】
　$\displaystyle 8(2-\sqrt{2})a^3 $
　

【解答のポイント】
本問は、断面積を積分して体積を求める問題です。

断面積から体積を求める問題では
　① 作図をする
　② 断面積を表す関数を作る
　③ 断面積を積分する
という過程で体積を求めます。

一方、本問では作図により具体的な形状を描こうとすると非常に難しくなります。

そこで、最初に直交する円柱の共通部分を表す以下のような不等式を作ります。 $$ \begin{dcases} & y^2 + z^2 \leqq a^2 \\[0.5em] & x^2 + z^2 \leqq a^2 \end{dcases} $$

この不等式に対して$\hspace{2pt}z=t\hspace{2pt}$における$\hspace{2pt}(x , y)\hspace{2pt}$の存在する範囲を図示すると、断面積$\hspace{2pt}S(t)\hspace{2pt}$を簡単に求めることができます。

求められた断面積$\hspace{1pt}S(t)\hspace{2pt}$を$\hspace{2pt}z\hspace{2pt}$方向の範囲で積分することで体積を求めます。
　

【問題(1)の解答】
　問題 :『中心軸に垂直な切り口の半径が$\hspace{1pt}a\hspace{1pt}$である無限に長い$\hspace{2pt}3\hspace{2pt}$本の直円柱をそれぞれ$\hspace{2pt}A , B , C\hspace{2pt}$とする. $A\hspace{1pt}$の中心軸が$\hspace{2pt}x\hspace{1pt}$軸, $B\hspace{1pt}$の中心軸が$\hspace{2pt}y\hspace{1pt}$軸, $C\hspace{1pt}$の中心軸が$\hspace{2pt}z\hspace{1pt}$軸であるとする.
　(1) $A , B\hspace{2pt}$の共通部分の体積を求めよ.
　(2) $A , B, C\hspace{2pt}$の共通部分の体積を求めよ.』
　

まず、$\hspace{2pt}2\hspace{2pt}$本の円柱が直交するときの共通部分を表す不等式を作ります。

中心が$\hspace{2pt}x\hspace{1pt}$軸の円柱の内側を表す不等式は $${y^2 + z^2 \leqq a^2}$$ 中心が$\hspace{2pt}y\hspace{1pt}$軸の円柱の内側を表す不等式は $${x^2 + z^2 \leqq a^2}$$ となります。

よって、$2\hspace{2pt}$本の円柱が直交するときに共通する部分は、以下の連立不等式によって表されます。 $$ \begin{dcases} & y^2 + z^2 \leqq a^2 \\[0.5em] & x^2 + z^2 \leqq a^2 \end{dcases} $$

ここで、$z = t\hspace{2pt}$の断面を考えます。上記の不等式は $$ \begin{aligned} y^2 + t^2 & \leqq a^2 \\[1em] x^2 + t^2 & \leqq a^2 \\ \end{aligned} $$ となります。

上式を整理すると$\hspace{2pt}(x,y)\hspace{2pt}$は以下の連立不等式を満たします。

$$ \begin{aligned} \hspace{10pt} - \sqrt{a^2 - t^2 } \leqq y & \leqq \sqrt{a^2 - t^2 } \hspace{10pt}\\[1em] - \sqrt{a^2 - t^2 } \leqq x & \leqq \sqrt{a^2 - t^2 } \\[1em] \end{aligned} $$

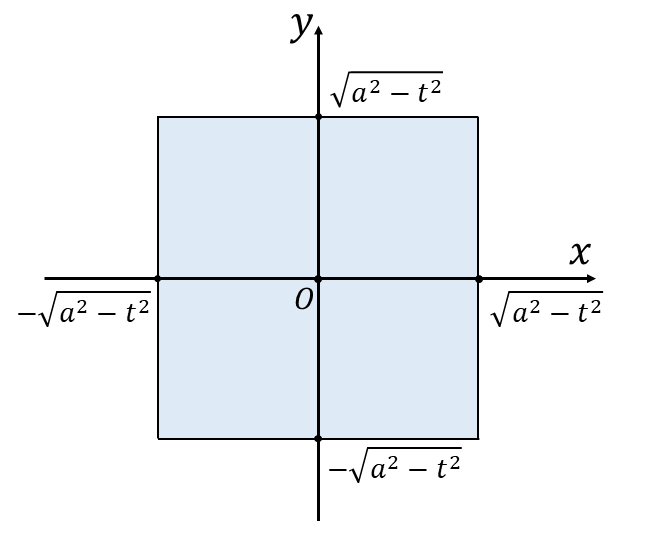
ここで、$z=t\hspace{2pt}$における$\hspace{2pt}(x,y)\hspace{2pt}$の範囲を図示すると、以下のようになります。 2本の直交する円柱の共通部分の体積の問題

つまり、$z = t\hspace{2pt}$の断面は一辺$\hspace{2pt}2\sqrt{a^2 - t^2 } \hspace{2pt}$の正方形となることが分かります。

したがって、断面積は $$ \begin{aligned} S(t) & = (2\sqrt{a^2 - t^2 })^2 \\[1em] & = 4(a^2 - t^2 ) \\ \end{aligned} $$ となります。

求める体積は、$S(t)\hspace{2pt}$を$\hspace{2pt}z\hspace{1pt}$の範囲である$\hspace{2pt}[-a , a]\hspace{2pt}$の区間で積分すればよいので $$ \begin{aligned} &\int_{-a}^a S(t) \hspace{1pt} dt \\[1em] & =4 \int_{-a}^a (a^2 - t^2 )\hspace{1pt} dt\\[1em] & =8 \int_{0}^a (a^2 - t^2 )\hspace{1pt} dt\\[1em] & =8 \left[ a^2 t - \frac{1}{3}t^3 \right]_{0}^a\\[1em] & = 8 \left(a^3 - \frac{1}{3}a^3 \right)\\[1em] & = \frac{16}{3}a^3 \\ \end{aligned} $$ と求められます。
　

【問題(2)の解答】
　問題 :『中心軸に垂直な切り口の半径が$\hspace{1pt}a\hspace{1pt}$である無限に長い$\hspace{2pt}3\hspace{2pt}$本の直円柱をそれぞれ$\hspace{2pt}A , B , C\hspace{2pt}$とする. $A\hspace{1pt}$の中心軸が$\hspace{2pt}x\hspace{1pt}$軸, $B\hspace{1pt}$の中心軸が$\hspace{2pt}y\hspace{1pt}$軸, $C\hspace{1pt}$の中心軸が$\hspace{2pt}z\hspace{1pt}$軸であるとする.
　(1) $A , B\hspace{2pt}$の共通部分の体積を求めよ.
　(2) $A , B, C\hspace{2pt}$の共通部分の体積を求めよ.』
　

まず、$\hspace{2pt}3\hspace{2pt}$本の円柱が直交するときの共通部分を表す不等式を作ります。

中心が$\hspace{2pt}x\hspace{1pt}$軸の円柱の内側を表す不等式は $${y^2 + z^2 \leqq a^2}$$ 中心が$\hspace{2pt}y\hspace{1pt}$軸の円柱の内側を表す不等式は $${x^2 + z^2 \leqq a^2}$$ 中心が$\hspace{2pt}z\hspace{1pt}$軸の円柱の内側を表す不等式は $${x^2 + y^2 \leqq a^2}$$ となります。

よって、$3\hspace{2pt}$本の円柱が直交するときに共通する部分は、以下の連立不等式によって表されます。 $$ \begin{dcases} & y^2 + z^2 \leqq a^2 \\[0.5em] & x^2 + z^2 \leqq a^2\\[0.5em] & x^2 + y^2 \leqq a^2 \end{dcases} $$

ここで、$z = t\hspace{2pt}$の断面を考えます。上記の不等式は $$ \begin{aligned} y^2 + t^2 & \leqq a^2 \hspace{2pt}\cdots (1)\\[1em] x^2 + t^2 & \leqq a^2 \hspace{2pt}\cdots (2)\\[1em] x^2 + y^2 & \leqq a^2 \hspace{2pt}\cdots (3) \end{aligned} $$ となります。

上式を整理すると$\hspace{2pt}(x,y)\hspace{2pt}$は以下の連立不等式を満たします。

$$ \begin{aligned} \hspace{10pt} - \sqrt{a^2 - t^2 } \leqq y & \leqq \sqrt{a^2 - t^2 } \hspace{2pt}\cdots (1') \hspace{10pt}\\[1em] - \sqrt{a^2 - t^2 } \leqq x & \leqq \sqrt{a^2 - t^2 } \hspace{2pt} \cdots (2')\\[1em] x^2 + y^2 & \leqq a^2 \cdots (3) \end{aligned} $$

式(1')と式(2')は、問題(1)と同じ一辺$\hspace{2pt}2\sqrt{a^2 - t^2 } \hspace{2pt}$の正方形の内側の領域を表します。

また、式(3)は半径$\hspace{1pt}a\hspace{1pt}$の円の内側の領域を表します。

ここで、式(1')と式(2')による正方形の内側の領域は$\hspace{2pt}t\hspace{2pt}$の値によって変化するため、$t\hspace{2pt}$の値によって正方形が(3)式の円に含まれるかどうかで場合分けをします。

式(3)の円の領域に(1')式と(2')式の正方形が含まれる条件を求めると

$${\hspace{10pt}x= \sqrt{a^2 - t^2 } ,\hspace{2pt}y= \sqrt{a^2 - t^2 } \hspace{10pt}}$$

が$\hspace{2pt}x^2 + y^2 \leqq a^2\hspace{2pt}$を満たせばよいので $${(\sqrt{a^2 - t^2 })^2 + (\sqrt{a^2 - t^2 })^2 \leqq a^2}$$ すなわち $${t^2 \geqq \frac{1}{2}a^2}$$ となります。

共通部分の対称性から$\hspace{2pt}z \geqq 0\hspace{2pt}$の範囲のみで考えると、積分区間は$\hspace{2pt}0 \leqq t \leqq a\hspace{2pt}$であり、上式を満たす$\hspace{2pt}t\hspace{2pt}$は$\displaystyle\frac{a}{\sqrt{2}} \leqq t \leqq a\hspace{2pt}$となります。

よって、$0 \leqq t \leqq a\hspace{2pt}$の範囲において、式(3)の円の領域に(1')式と(2')式の正方形が含まれるかどうかで場合分けすると

　[1] $\displaystyle\frac{a}{\sqrt{2}} \leqq t \leqq a\hspace{2pt}$

　[2] $\displaystyle 0 \leqq t \leqq \frac{a}{\sqrt{2}} \hspace{2pt}$

となります。
　

[1] $\displaystyle\frac{a}{\sqrt{2}} \leqq t \leqq a\hspace{2pt}$のとき

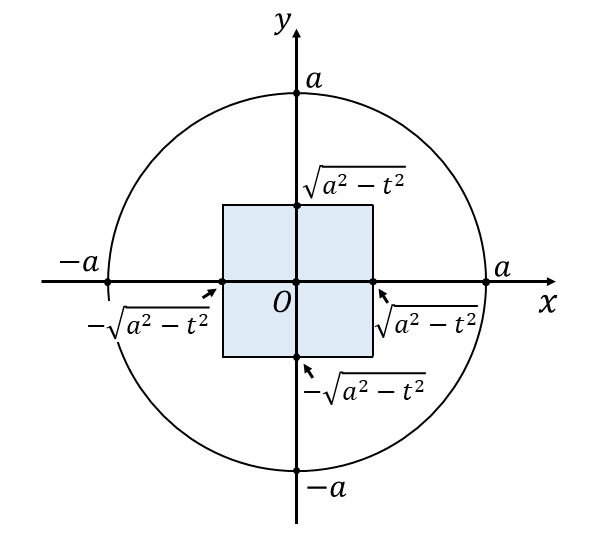
　このとき、式(3)の示す円の領域に(1')式と(2')式の正方形が含まれており、$z=t\hspace{2pt}$における$\hspace{2pt}(x,y)\hspace{2pt}$の範囲は以下の青く塗られた領域となります。 3本の直交する円柱の共通部分の体積の問題

$\displaystyle \frac{a}{\sqrt{2}} \leqq t \leqq a\hspace{2pt}$における断面積$\hspace{2pt}S(t)\hspace{2pt}$は、問題(1)と同様に $${S(t)=4(a^2 - t^2 )}$$ となります。

よって、$\displaystyle \frac{a}{\sqrt{2}} \leqq t \leqq a \hspace{2pt}$における体積$\hspace{2pt}V_1\hspace{2pt}$は $$ \begin{aligned} V_1 & = \int_{\frac{a}{\sqrt{2}}}^a S(t) \hspace{1pt} dt \\[1em] & =4 \int_{\frac{a}{\sqrt{2}}}^a (a^2 - t^2 )\hspace{1pt} dt\\[1em] & =4 \left[ a^2 t - \frac{1}{3}t^3 \right]_{\frac{a}{\sqrt{2}}}^a\\[1em] & = \left( \frac{8}{3} - \frac{5}{3}\sqrt{2}\right)a^3 \\ \end{aligned} $$ となります。
　

[2] $\displaystyle 0 \leqq t \leqq \frac{a}{\sqrt{2}}\hspace{2pt}$のとき

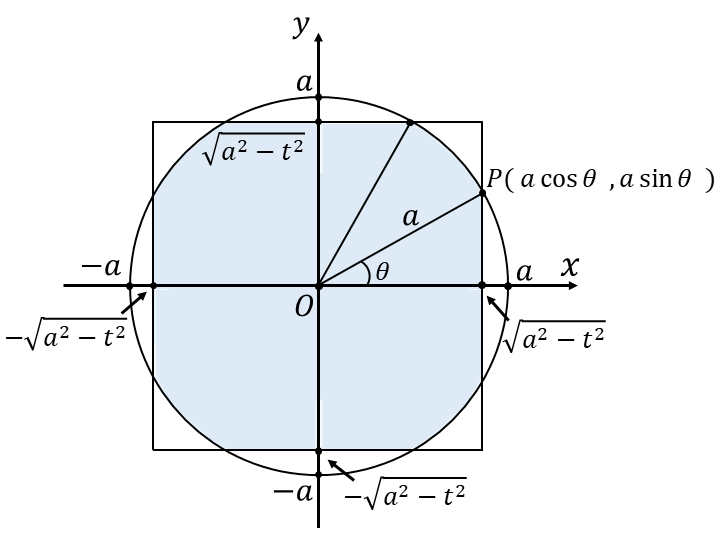
　このとき、式(3)の示す円の領域に(1')式と(2')式の正方形が含まれず、$z=t\hspace{2pt}$における$\hspace{2pt}(x,y)\hspace{2pt}$の範囲は以下の青く塗られた領域となります。 3本の直交する円柱の共通部分の体積の問題

図の正方形と円の交点を点$\hspace{1pt}P\hspace{2pt}$とします。
また、線分$\hspace{1pt}OP\hspace{1pt}$と$\hspace{2pt}x\hspace{1pt}$軸のなす角度を$\hspace{2pt}\theta\hspace{2pt}$とします。

$\hspace{1pt}t\hspace{2pt}$と$\hspace{2pt}\theta\hspace{2pt}$の関係を求めると $$ \begin{aligned} \sqrt{a^2 - t^2} & = a \cos \theta\\[0.5em] a^2 - t^2 & = a^2 \cos^2 \theta\\[0.5em] a^2 - t^2 & =a^2(1- \sin^2 \theta) \\[0.5em] t^2 & = a^2 \sin^2 \theta\\[0.5em] \end{aligned}$$ よって、$\displaystyle 0 \leqq t \leqq \frac{a}{\sqrt{2}}\hspace{2pt}$のとき $$ t = a \sin \theta $$ となります。

ここで、両辺を$\hspace{2pt}\theta\hspace{2pt}$で微分すると、$\displaystyle \frac{d t}{d \theta} = a \cos \theta\hspace{2pt}$であることから、$dt = a \cos \theta d \theta\hspace{2pt}$と表せます。

上図から、$\displaystyle 0 \leqq t \leqq \frac{a}{\sqrt{2}} \hspace{2pt}$における断面積$\hspace{2pt}S(t)\hspace{2pt}$は

$$ \begin{aligned} \hspace{15pt} S(t) & = 4 \left \{2 \cdot \frac{1}{2}\cdot a \cos \theta \cdot a \sin \theta + \frac{1}{2}a^2\left( \frac{\pi}{2} - 2 \theta\right) \right\} \hspace{15pt} \\[1em] & =a^2 (4 \cos \theta \sin \theta + \pi -4 \theta)\\[1em] \end{aligned} $$

よって、$S(t)\hspace{2pt}$を$\displaystyle \hspace{2pt}\left[0 , \frac{a}{\sqrt{2}}\right]\hspace{2pt}$の区間で積分すると体積$\hspace{1pt}V_2\hspace{1pt}$は

$$ \begin{aligned} \hspace{15pt} V_2 =&\int_{0}^\frac{a}{\sqrt{2}} S(t) \hspace{1pt} dt \\[1em] & =a \int_{0}^\frac{\pi}{4} S(t) \cos \theta \hspace{1pt} d \theta\\[1em] & =a^3 \int_{0}^\frac{\pi}{4} \{4 \cos \theta \sin \theta + \pi -4 \theta\}\cos \theta\hspace{1pt} d \theta\\[1em] & =a^3 \int_{0}^\frac{\pi}{4} \{4 \cos^2 \theta \sin \theta + \pi \cos \theta -4 \theta \cos \theta\}\hspace{1pt} d \theta\\[1em] \end{aligned} $$

ここで、$\displaystyle \int_{0}^\frac{\pi}{4}4\cos^2 \theta \sin \theta d\theta\hspace{2pt}$を求めます。

置換積分法より $${u = \cos \theta}$$ とおくと、$\displaystyle \frac{du}{d\theta} = - \sin \theta\hspace{2pt}$より$\hspace{2pt}du = - \sin \theta d \theta\hspace{2pt}$と表せます。

また、変数$\hspace{2pt}\theta\hspace{2pt}$と$\hspace{2pt}u\hspace{2pt}$の積分区間は以下のように対応します。

${\theta}$	${\displaystyle 0 \to \frac{\pi}{4}}$
${u}$	$\displaystyle{1 \to \frac{1}{\sqrt{2}}}$

以上から $$ \begin{aligned} \hspace{15pt} & \int_{0}^\frac{\pi}{4}4 \cos^2 \theta \sin \theta d\theta \\[1em] & = -4\int_{1}^\frac{1}{\sqrt{2}} u^2 du\\[1em] & = - 4\left[ \frac{1}{3}u^3\right]_{1}^\frac{1}{\sqrt{2}}\\[1em] & = - 4\cdot \frac{1}{3}\left(\frac{1}{2\sqrt{2}}-1 \right)\\[1em] & = \frac{4-\sqrt{2} }{3} \\[1em] \end{aligned} $$

また、$\displaystyle \int_{0}^\frac{\pi}{4}\pi\cos \theta d\theta\hspace{2pt}$を求めると $$ \begin{aligned} \hspace{15pt} & \int_{0}^\frac{\pi}{4}\pi\cos \theta d\theta \\[1em] & = \pi\left[\sin \theta \right]_{0}^\frac{\pi}{4}\\[1em] & = \frac{\sqrt{2}}{2}\pi\\[1em] \end{aligned} $$ となります。

また、$\displaystyle \int_{0}^\frac{\pi}{4}-4\theta \cos \theta d\theta\hspace{2pt}$を求めると、部分積分から $$ \begin{aligned} \hspace{15pt} & -4 \int_{0}^\frac{\pi}{4}\theta \cos \theta d\theta \\[1em] & = -4 \left\{\left[\theta \sin \theta \right]_{0}^\frac{\pi}{4} - \int_{0}^\frac{\pi}{4}\sin \theta d\theta \right\}\\[1.3em] & = -4 \left \{\frac{\pi}{4}\cdot \frac{\sqrt{2}}{2} + \left[ \cos \theta \right]_{0}^\frac{\pi}{4} \right \}\\[1.3em] & = -4 \left \{\frac{\sqrt{2}}{8}\pi+ \frac{\sqrt{2}}{2} -1\right \}\\[1.3em] & = 4-\frac{\sqrt{2}}{2}\pi -2\sqrt{2} \\ \end{aligned} $$ となります。

よって、体積$\hspace{1pt}V_2\hspace{1pt}$は

$$ \begin{aligned} \hspace{15pt} V_2 =&a^3 \int_{0}^\frac{\pi}{4} \{4 \cos^2 \theta \sin \theta + \pi \cos \theta -4 \theta \cos \theta\}\hspace{1pt} d \theta\\[1em] & = a^3 \left \{ \frac{4-\sqrt{2} }{3} + \frac{\sqrt{2}}{2}\pi + 4-\frac{\sqrt{2}}{2}\pi -2\sqrt{2}\right \}\\[1em] & = \left( \frac{16}{3} -\frac{7\sqrt{2}}{3}\right )a^3 \end{aligned} $$

したがって、求める体積は $$ \begin{aligned} V & = 2(V_1 + V_2) \\[1em] & =8(2-\sqrt{2})a^3\\[1em] \end{aligned} $$ となります。
($\hspace{2pt}V_1 , V_2\hspace{2pt}$は$\hspace{2pt}0 \leqq t \leqq a\hspace{2pt}$の範囲で体積を求めたので、求める体積は$\hspace{2pt}V_1 + V_2\hspace{2pt}$を$\hspace{1pt}2\hspace{2pt}$倍しています。)
　

【入試本番に向けたアドバイス】
本問は、直交する円柱の共通部分を不等式で表し、体積を求める問題です。

断面積から体積を求める問題では

　① 作図をする
　② 断面積を表す関数を作る
　③ 断面積を積分する

という過程で体積を求めます。
　

しかし、本問のように求める立体を作図することが難しい場合は

　① 連立不等式を作る
　② $x = t \hspace{1pt},\hspace{1pt} y = t \hspace{1pt},\hspace{1pt} z = t\hspace{2pt}$のいずれかを選び、$t\hspace{2pt}$を定数とした連立不等式に変形する
　③ ②の連立不等式から断面積$\hspace{1pt}S(t)\hspace{2pt}$を求める
　④ 断面積を$\hspace{2pt}t\hspace{2pt}$の範囲で積分する

という過程で体積を求めます。

連立不等式から断面積を考えるときに、立体の切り方として $${x = t \hspace{1pt},\hspace{1pt} y = t \hspace{1pt},\hspace{1pt} z = t}$$ の3つの選択肢があります。

断面を切る文字の選び方としては、『その断面で切ると残りの文字の対称性が良くなる』や『その断面で切ると残りの文字の次数が小さくなる』ような文字を優先して$\hspace{2pt}t\hspace{2pt}$とおきます。

例えば、本問では問題(1)で$\hspace{1pt}x\hspace{1pt}$軸が中心軸の円柱と$\hspace{1pt}y\hspace{1pt}$軸が中心軸の円柱の共通部分の体積を求めるために、$z =t\hspace{2pt}$で切ることで残りの文字が$\hspace{2pt}(x,y)\hspace{2pt}$となり対称性が良くなります。

断面を切る文字の選ぶときは『その後の計算がより簡単になる文字』を意識して選ぶようにしましょう。
　

【関連するページ】
・定積分

・置換積分法

・部分積分
　

\({\theta}\)	\({\displaystyle 0 \to \frac{\pi}{4}}\)
\({u}\)	\(\displaystyle{1 \to \frac{1}{\sqrt{2}}}\)