分母に二次関数(x^2+3x+3)を含む角度が具体的に求められない定積分の問題と解き方

【答え】
　$\displaystyle \frac{10\sqrt{7}-14\sqrt{3}}{21} $
　

【解答のポイント】
　本問のように分母に二次関数$\hspace{2pt}ax^2+bx+c\hspace{2pt}$が含まれており、かつ部分分数分解が使えない場合は二次関数を平方完成して置き換える方法が有効です。

分母の二次関数$\hspace{2pt}x^2+3x+3\hspace{2pt}$を平方完成して置換積分ができる $${(x+p)^2 + a^2}$$ の式に変形し、${x+p =a \tan \theta \hspace{2pt}}$と置き換えて積分します。
　

ここで、変数${\hspace{2pt}x\hspace{2pt}}$の範囲に対応する変数${\hspace{2pt}\theta\hspace{2pt}}$を求めると、$x=1\hspace{2pt}$のとき$\displaystyle{\hspace{4pt}\frac{5}{\sqrt{3}}= \tan \theta \hspace{2pt}}$となり、$\theta\hspace{2pt}$の値を求めることができません。

そこで、上式を満たす$\hspace{2pt}\theta\hspace{2pt}$を$\hspace{2pt}\alpha\hspace{2pt}$$\displaystyle\hspace{2pt}(-\frac{\pi}{2} < \alpha < \frac{\pi}{2})\hspace{2pt}$とおき、そのまま定積分の計算を進めます。

$\displaystyle{\frac{5}{\sqrt{3}}= \tan \alpha \hspace{2pt}}$から$\hspace{2pt}\sin \alpha\hspace{2pt}$の値が得られることから、$\alpha\hspace{2pt}$の具体的な値が分からなくても定積分の値を求めることができます。
　

【解答】
　問題 :『定積分$\displaystyle\hspace{2pt} \int_0^1 \frac{1}{(x^2+3x+3)^{\frac{3}{2}} }\hspace{1pt}dx\hspace{2pt}$を求めよ』
　

被積分関数の分母に含まれる$\hspace{2pt}x^2+3x+3\hspace{2pt}$を平方完成して変形すると

$$ \begin{aligned} \hspace{10pt}& \int_0^1 \frac{1}{(x^2+3x+3)^{\frac{3}{2}} }\hspace{1pt}dx \\[1em] & = \int_0^1 \frac{1}{\left(\left(x+\frac{3}{2}\right)^2 + \frac{3}{4}\right)^{\frac{3}{2}} }\hspace{1pt}dx \\[1em] & = \int_0^1 \frac{1}{\left(\left(x+\frac{3}{2}\right)^2 +\left(\frac{\sqrt{3}}{2}\right)^2\right)^{\frac{3}{2}} }\hspace{1pt}dx \\[1em] \end{aligned} $$

となります。

ここで $\displaystyle{x+\frac{3}{2}= \frac{\sqrt{3}}{2} \tan \theta}$$\displaystyle\hspace{4pt}(-\frac{\pi}{2} < \theta < \frac{\pi}{2})\hspace{2pt}$とおきます。

変数${\hspace{2pt}t\hspace{2pt}}$の範囲に対応する変数${\hspace{2pt}\theta\hspace{2pt}}$を求めると、以下のようになります。

${x}$	${0 \to 1}$
${\theta}$	$\displaystyle{\frac{\pi}{3} \to \alpha}$

ここで、$\alpha\hspace{2pt}$は$\displaystyle{\hspace{4pt}\frac{5}{\sqrt{3}}= \tan \alpha \hspace{2pt}}$$\displaystyle\hspace{2pt}(-\frac{\pi}{2} < \alpha < \frac{\pi}{2})\hspace{2pt}$を満たす値となります。

また、$\displaystyle{x +\frac{3}{2}= \frac{\sqrt{3}}{2} \tan \theta}$ の両辺を ${\theta}$ で微分すると、三角関数の微分公式から $${\frac{dx}{d\theta} = \frac{\sqrt{3}}{2\cos^2 \theta} }$$ となります。すなわち、$\displaystyle{dx = \frac{\sqrt{3}}{2\cos^2 \theta} \hspace{1pt} d\theta}$ と表せます。

変数を置き換えて積分すると

$$ \begin{aligned} \hspace{10pt}& \int_0^1 \frac{1}{\left(\left(x+\frac{3}{2}\right)^2 +\left(\frac{\sqrt{3}}{2}\right)^2\right)^{\frac{3}{2}} }\hspace{1pt}dx \\[1.4em] &= \int_\frac{\pi}{3}^{\alpha} \frac{1}{\left(\frac{3}{4}\tan^2 \theta +\frac{3}{4}\right)^{\frac{3}{2}} }\cdot \frac{\sqrt{3}}{2\cos^2 \theta} \hspace{1pt} d\theta\hspace{10pt}\\[1.4em] &= \int_\frac{\pi}{3}^{\alpha} \frac{1}{\frac{3\sqrt{3}}{8}\left(\tan^2 \theta +1\right)^{\frac{3}{2}} }\cdot \frac{\sqrt{3}}{2\cos^2 \theta} \hspace{1pt} d\theta\hspace{10pt}\\[1.4em] &= \frac{4}{3}\int_\frac{\pi}{3}^{\alpha} \frac{1}{\left(\tan^2 \theta +1\right)^{\frac{3}{2}} }\cdot \frac{1}{\cos^2 \theta} \hspace{1pt} d\theta\hspace{10pt}\\[1.4em] &= \frac{4}{3}\int_\frac{\pi}{3}^{\alpha} \cos^3 \theta \cdot \frac{1}{\cos^2 \theta} \hspace{1pt} d\theta\hspace{10pt}\\[1.4em] &= \frac{4}{3}\int_\frac{\pi}{3}^{\alpha} \cos \theta \hspace{1pt} d\theta\hspace{10pt}\\[1.4em] &= \frac{4}{3} \left[\sin \theta \right]_\frac{\pi}{3}^{\alpha} \hspace{10pt}\\[1.4em] &= \frac{4}{3} \left(\sin \alpha - \frac{\sqrt{3}}{2} \right) \hspace{10pt}\\[1.4em] \end{aligned} $$

となります。

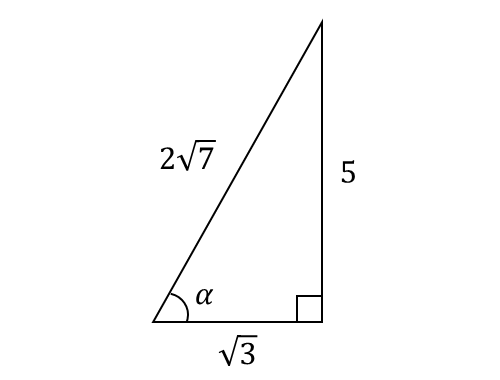
ここで、$\displaystyle{\frac{5}{\sqrt{3}}= \tan \alpha \hspace{2pt}}$を満たす角度$\hspace{1pt} \alpha\hspace{1pt}$を持つ直角三角形の三辺は以下の図のようになります。定積分の問題における直角三角形の三辺

よって、$\displaystyle\sin \alpha = \frac{5}{2\sqrt{7}}\hspace{2pt}$となります。

したがって

$$ \begin{aligned} & \frac{4}{3} \left(\sin \alpha - \frac{\sqrt{3}}{2} \right) \hspace{10pt}\\[1.4em] &= \frac{4}{3} \left(\frac{5}{2\sqrt{7}} - \frac{\sqrt{3}}{2} \right) \hspace{10pt}\\[1.4em] &= \frac{10\sqrt{7}-14\sqrt{3}}{21} \\[1.4em] \end{aligned} $$

と求められます。
　

【関連するページ】
・置換積分
　

\({x}\)	\({0 \to 1}\)
\({\theta}\)	\(\displaystyle{\frac{\pi}{3} \to \alpha}\)

(x^2+3x+3)を含む定積分