三次関数と接線に囲まれた面積の範囲を求める問題

【問題(1)の答え】
　$\hspace{1pt} a > 0 , a < -1\hspace{1pt}$のとき$\hspace{2pt}1\hspace{1pt}$本

　$\hspace{1pt} a = 0 , -1 \hspace{1pt}$のとき$\hspace{2pt}2\hspace{1pt}$本

　$\hspace{1pt} -1 < a < 0 \hspace{1pt}$のとき$\hspace{2pt}3\hspace{1pt}$本

【問題(2)の答え】
　$\displaystyle S > \frac{27}{64}\hspace{2pt}$
　

【解答のポイント】
問題(1)は、曲線の外の点から引かれた接線の本数を求める問題です。

このような三次関数の接線の本数を求める問題は

　① 曲線${\hspace{2pt}y=f(x)\hspace{2pt}}$上の接点を ${(t,f(t))}$ とおき、$x=t\hspace{2pt}$における接線の方程式を求める
　② 接線の方程式が曲線の外の点を通る条件式を求める
　③ ②で得られた$\hspace{2pt}t\hspace{2pt}$の方程式の解の個数から、接線の本数を求める

という手順で接線の本数を調べます。
　

本問では、三次方程式$\hspace{2pt}-2t^3 +3t^2 -1-a = 0\hspace{2pt}$が得られることから、定数分離法を用いて $$ \begin{dcases} y =& -2t^3 +3t^2 -1 \\[0.5em] y= & a\\[0.5em] \end{dcases} $$ の連立方程式の解の個数から、接線の本数を調べます。
　

問題(2)では、まず接線の本数が$\hspace{2pt}1\hspace{1pt}$本であるときの接点$\hspace{2pt} t \hspace{2pt}$の範囲を求めます。

次に、接線と曲線$\hspace{1pt}C\hspace{2pt}$の交点の$\hspace{2pt}x\hspace{1pt}$座標を$\hspace{2pt}t\hspace{2pt}$で表します。

定積分から計算される面積を$\hspace{2pt}t\hspace{2pt}$により表し、接点$\hspace{2pt} t \hspace{2pt}$の範囲から面積$\hspace{1pt}S\hspace{2pt}$の範囲を示します。
　

【問題(1)の解答】
　問題 : 『次の問いに答えよ.
　(1) 直線$\hspace{2pt}x=1\hspace{2pt}$上を移動する点から曲線$\hspace{2pt}C : y = x^3 -2x+1\hspace{2pt}$に引ける接線の本数を調べよ.
　(2) 問題(1)において接線の本数が$\hspace{2pt}1\hspace{1pt}$本であるとき, 直線$\hspace{2pt}x=1\hspace{2pt}$上の点から曲線$\hspace{2pt}C\hspace{2pt}$に引いた接線と曲線$\hspace{2pt}C\hspace{2pt}$によって囲まれる面積$\hspace{1pt}S\hspace{2pt}$の取りうる範囲を求めよ.』
　

まず、曲線${\hspace{2pt}y=f(x)\hspace{2pt}}$上の接点を ${(t,t^3-2t+1)}$ とおき、この接点における接線の方程式を求めます。

$\displaystyle {f(x)=x^3 -2x+1}$ を微分すると $${f'(x)=3x^2-2}$$ となります。

${(t,t^3-2t+1)\hspace{2pt}}$における接線は $${y - (t^3-2t+1) = (3t^2-2)(x-t)}$$ すなわち $$ \begin{aligned} y & = (3t^2-2)(x-t) + t^3-2t+1 \\[0.5em] &= (3t^2-2)x -2t^3+1 \cdots(1)\\[0.5em] \end{aligned} $$ と求められます。
　

次に、(1)式の接線の方程式が直線$\hspace{2pt}x=1\hspace{2pt}$上を移動する点を通るときの条件式を求めます。

直線$\hspace{2pt}x=1\hspace{2pt}$上を移動する点を$\hspace{2pt}(1,a)\hspace{2pt}$とします。

(1)式の接線が点${\hspace{1pt}(1,a)\hspace{2pt}}$を通るとき $${a = (3t^2-2)\cdot 1 -2t^3+1}$$ 式を整理すると $${-2t^3 +3t^2 -1-a = 0\cdots(2)}$$ となります。

(2)式の三次方程式の解の個数が、点$\hspace{1pt}(1,a)\hspace{1pt}$から曲線に引ける接線の本数と一致します。

ここで、定数分離法から(2)式の解の個数を求めます。

(2)式の解の個数は以下の連立方程式 $$ \begin{dcases} y =& -2t^3 +3t^2 -1 \\[0.5em] y= & a\\[0.5em] \end{dcases} $$ の解の個数と一致します。

$\displaystyle {g(t)=-2t^3 +3t^2 -1}$ とおき、微分すると $$ \begin{aligned} g'(t) & = -6t^2+6t\\[0.7em] &= -6t(t-1)\\[0.5em] \end{aligned} $$ となります。

よって、${g'(t)=0}$ の解は$\hspace{2pt}t = 0 , 1\hspace{2pt}$となります。

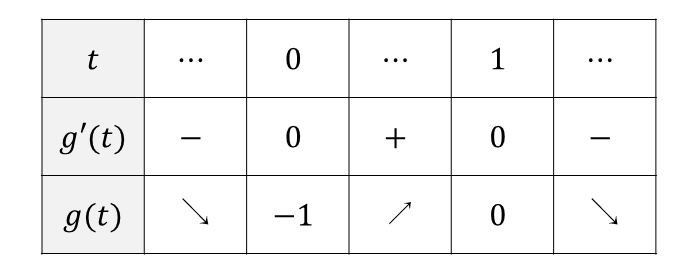
$g(t)=-2t^3 +3t^2 -1\hspace{2pt}$の増減表を作成すると以下のようになります。 g(x)=-2t^3 +3t^2 -1の増減表
　

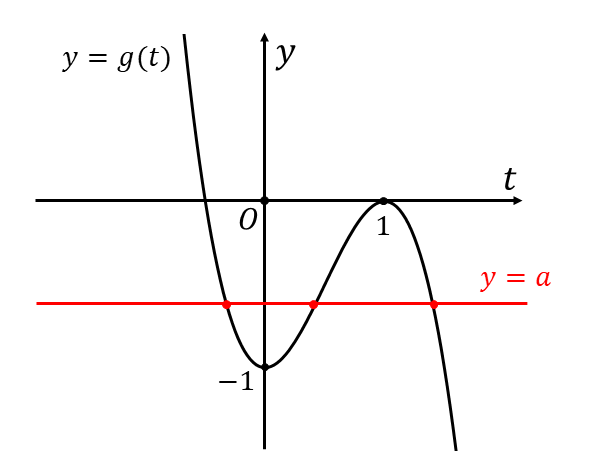
よって、$y=g(t)\hspace{2pt}$のグラフを描くと以下のようになります。 g(x)=-2t^3 +3t^2 -1のグラフ
　

$y=g(t)\hspace{2pt}$と$\hspace{2pt}y=a\hspace{2pt}$の共有点の個数が(2)式の実数解の個数となるため、求める接線の本数は定数$\hspace{1pt}a\hspace{1pt}$によって以下のようになります。

　$\hspace{1pt} a > 0 , a < -1\hspace{1pt}$のとき$\hspace{2pt}1\hspace{1pt}$本

　$\hspace{1pt} a = 0 , -1 \hspace{1pt}$のとき$\hspace{2pt}2\hspace{1pt}$本

　$\hspace{1pt} -1 < a < 0 \hspace{1pt}$のとき$\hspace{2pt}3\hspace{1pt}$本
　

【問題(2)の解答】
　問題 : 『次の問いに答えよ.
　(1) 直線$\hspace{2pt}x=1\hspace{2pt}$上を移動する点から曲線$\hspace{2pt}C : y = x^3 -2x+1\hspace{2pt}$に引ける接線の本数を調べよ.
　(2) 問題(1)において接線の本数が$\hspace{2pt}1\hspace{1pt}$本であるとき, 直線$\hspace{2pt}x=1\hspace{2pt}$上の点から曲線$\hspace{2pt}C\hspace{2pt}$に引いた接線と曲線$\hspace{2pt}C\hspace{2pt}$によって囲まれる面積$\hspace{1pt}S\hspace{2pt}$の取りうる範囲を求めよ.』
　

問題(1)の結果から、接線の本数が$\hspace{2pt}1\hspace{1pt}$本であるとき$\hspace{2pt} a > 0 , a < -1 \hspace{2pt}$となります。

ここで、$\hspace{2pt} a > 0 , a < -1 \hspace{2pt}$を満たす接点$\hspace{2pt}t\hspace{2pt}$の範囲を求めます。
　

[1]$\hspace{2pt} a > 0 \hspace{2pt}$における$\hspace{2pt}t\hspace{2pt}$の範囲
　$\hspace{2pt}a = 0\hspace{2pt}$のとき、(2)式を満たす$\hspace{2pt}t\hspace{2pt}$の値を求めると $$\begin{aligned} \hspace{10pt} -2t^3 +3t^2 -1 & = 0\\[0.5em] -(t-1)^2(2t+1) & = 0\\ \end{aligned} $$ から、$\displaystyle t = 1 , -\frac{1}{2}\hspace{2pt}$となります。

(上記の式変形は、$y=g(x)\hspace{2pt}$のグラフが$\hspace{1pt}x=1\hspace{1pt}$に接点を持つことから、$-2t^3 +3t^2 -1 \hspace{2pt}$を$\hspace{2pt}(t-1)^2\hspace{2pt}$で割ると$\hspace{2pt}(-2t-1)\hspace{2pt}$となることより因数分解しています。)

したがって、問題(1)のグラフから$\hspace{2pt} a > 0 \hspace{2pt}$における$\hspace{2pt}t\hspace{2pt}$の範囲は $${t < -\frac{1}{2}}$$ となります。
　

[2]$\hspace{2pt} a < -1 \hspace{2pt}$における$\hspace{2pt}t\hspace{2pt}$の範囲
　$\hspace{2pt}a = -1\hspace{2pt}$のとき、(2)式を満たす$\hspace{2pt}t\hspace{2pt}$の値を求めると $$\begin{aligned} \hspace{10pt} -2t^3 +3t^2 & = 0\\[0.5em] -t^2(2t-3) & = 0\\ \end{aligned} $$ から、$\displaystyle t = 0 , \frac{3}{2}\hspace{2pt}$となります。

したがって、問題(1)のグラフから$\hspace{2pt} a < -1 \hspace{2pt}$における$\hspace{2pt}t\hspace{2pt}$の範囲は $${t > \frac{3}{2}}$$ となります。

[1]と[2]から、$\hspace{2pt} a > 0 , a < -1 \hspace{2pt}$を満たす接点$\hspace{2pt}t\hspace{2pt}$の範囲は $${t < -\frac{1}{2} , t > \frac{3}{2}}$$ となります。
　

次に、曲線$\hspace{2pt}C : y = x^3 -2x+1\hspace{2pt}$と接線$\hspace{1pt}y=(3t^2-2)x -2t^3+1\hspace{1pt}$の交点の$\hspace{2pt}x\hspace{2pt}$座標を求めると

$$\begin{aligned} \hspace{10pt}x^3 -2x+1 & = (3t^2-2)x -2t^3+1 \hspace{10pt}\\[0.5em] x^3 -3t^2 x + 2t^3 & = 0\\[0.5em] (x-t)^2(x+2t) & = 0\\ \end{aligned} $$

であることから、$x = t , -2t\hspace{2pt}$となります。

(上記の式変形は、曲線$\hspace{1pt}C\hspace{2pt}$と接線が$\hspace{1pt}x=t\hspace{1pt}$に接点を持つことから、$x^3 -3t^2 x + 2t^3 \hspace{2pt}$を$\hspace{2pt}(x-t)^2\hspace{2pt}$で割ると$\hspace{2pt}(x+2t)\hspace{2pt}$となることより因数分解しています。)

したがって、直線$\hspace{2pt}x=1\hspace{2pt}$上の点から曲線$\hspace{2pt}C\hspace{2pt}$に引いた接線と曲線$\hspace{2pt}C\hspace{2pt}$によって囲まれる面積$\hspace{1pt}S\hspace{2pt}$を求めると、以下のようになります。

$$\begin{aligned} \hspace{10pt} S = & \left | \int_{-2t}^t \left \{ x^3 -2x+1 - \left((3t^2-2)x -2t^3+1 \right)\right \} \hspace{1pt}dx \right |\hspace{10pt}\\[1.2em] \hspace{10pt} =& \left | \int_{-2t}^t (x-t)^2(x+2t) \hspace{1pt}dx \right |\hspace{10pt}\\[1.2em] \hspace{10pt} =& \left | \int_{-2t}^t \left \{(x-t)^2(x-t + 3t) \right\} \hspace{1pt}dx \right |\hspace{10pt}\\[1.2em] \hspace{10pt} =& \left | \int_{-2t}^t \left \{(x-t)^3 + 3t (x-t)^2 \right\} \hspace{1pt}dx \right |\hspace{10pt}\\[1.2em] \hspace{10pt} =& \left | \left [ \frac{1}{4}(x-t)^4 +3t \cdot \frac{1}{3}(x-t)^3\right ]_{-2t}^t \right |\hspace{10pt}\\[1.2em] \hspace{10pt} =& \frac{27}{4}t^4\hspace{10pt}\\[1.2em] \end{aligned} $$

ここで、$t\hspace{2pt}$の範囲が$\displaystyle\hspace{2pt}t < -\frac{1}{2} , t > \frac{3}{2}\hspace{2pt}$であることから、$\displaystyle t^4 > \frac{1}{16}\hspace{2pt}$となります。

したがって、求める面積の値の範囲は$\displaystyle\hspace{2pt}\frac{27}{4} \times \frac{1}{16} = \frac{27}{64}\hspace{2pt}$より、$\displaystyle S > \frac{27}{64}\hspace{2pt}$となります。
　

【入試本番に向けたアドバイス】
　本問は、前半が『接線の本数を調べる問題』、後半が『接線と曲線に囲まれた面積を求める問題』となっています。

三次関数の接線の本数は以下の手順で求められます。

接線の本数は、本問のように積分の問題と合わせて出題されることが多いです。
計算量も多くなるので、手順をすぐに思い出せるように練習しておきましょう。
　

後半の積分は、接線の本数が$\hspace{2pt}1\hspace{1pt}$本となるときの接点の$\hspace{2pt}x\hspace{1pt}$座標$\hspace{2pt}x=t\hspace{2pt}$の範囲を求め、面積を$\hspace{2pt}t\hspace{1pt}$で表すことで面積の範囲を求めます。

$\hspace{2pt}t\hspace{1pt}$の値によって三次関数と接線の上下関係は変化しますが、絶対値付きの定積分を計算することで場合分けをしなくても面積を求めることができます。

計算の途中で以下のように被積分関数を変形して計算を行いました。 $$\begin{aligned} & \int_{-2t}^t (x-t)^2(x+2t) \hspace{1pt}dx\\[1.2em] &= \int_{-2t}^t \left \{(x-t)^2(x-t + 3t) \right\} \hspace{1pt}dx \\[1.2em] &= \int_{-2t}^t \left \{(x-t)^3 + 3t (x-t)^2 \right\} \hspace{1pt}dx \\[1.2em] \end{aligned} $$

このように式変形すると

$${\hspace{10pt}\int (x-t)^3 } \hspace{1pt}dx = \frac{1}{4}(x-t)^4 +C \hspace{10pt}$$

などの簡単な積分の和になるため、式展開する手間を省くことができ、計算時間を短縮できます。
　

【関連するページ】
・定積分
　