ガウス記号の含まれた定積分の問題

【問題(1)の答え】

　

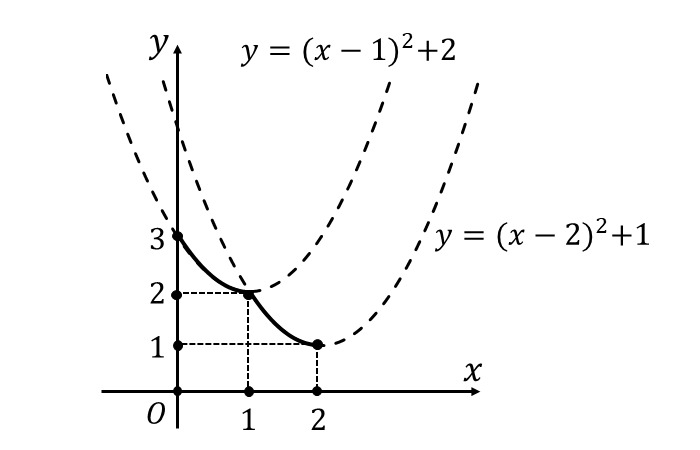
【問題(2)の答え】
　\(\displaystyle\hspace{2pt}\frac{11}{3}\hspace{2pt}\)
　

【解答のポイント】
本問は、ガウス記号が積分に含まれる定積分の問題です。

被積分関数に含まれる\( \hspace{2pt} [x]\hspace{2pt}\)は\(\hspace{2pt}n \leqq x\hspace{2pt}\)を満たす最大の整数\(\hspace{2pt}n\hspace{2pt}\)を表します。

例えば、\([1.6]\hspace{2pt}\)は\(\hspace{2pt}n \leqq 1.6\hspace{2pt}\)を満たす最大の整数であるので $${[1.6] = 1}$$ となります。

また、\([2]\hspace{2pt}\)は\(\hspace{2pt}n \leqq 2\hspace{2pt}\)を満たす最大の整数であるので $${[2] = 2}$$ となります。

一般的には、\(x\hspace{2pt}\)を実数、\(\hspace{1pt}n\hspace{2pt}\)を整数とすると\(\hspace{2pt}n \leqq x < n+1\hspace{2pt}\)であるとき $${[x]=n}$$ となります。

本問は、\(\hspace{2pt}0 \leqq x \leqq 2\hspace{2pt}\)の範囲でグラフを描くため、\(\hspace{2pt}[x]\hspace{2pt}\)の値ごとに以下のように場合分けをすることで、ガウス記号を外します。

　[1] \(\hspace{2pt}0 \leqq x < 1\hspace{2pt}\)のとき
　[2] \(\hspace{2pt}1 \leqq x < 2\hspace{2pt}\)のとき
　[3] \(\hspace{2pt} x = 2\hspace{2pt}\)のとき
　

【問題(1)の解答】
　問題 : 『関数\(\hspace{2pt}f(x)\hspace{2pt}\)を\(\hspace{2pt}f(x)=(x-[x])^2-2(x-[x])+3-[x]\hspace{2pt}\)とする. ここで\( \hspace{1pt},\hspace{1pt} [x]\hspace{2pt}\)は\(\hspace{2pt}n \leqq x\hspace{2pt}\)を満たす最大の整数\(\hspace{2pt}n\hspace{2pt}\)を表す.
　(1) \(0 \leqq x \leqq 2\hspace{2pt}\)における\(\hspace{2pt}y = f(x)\hspace{2pt}\)のグラフをかけ.
　(2) \(\displaystyle\hspace{2pt}\int_0^2 f(x) \hspace{1pt}dx\hspace{2pt}\)を求めよ.』
　

ガウス記号の性質から整数\(\hspace{1pt}n\hspace{2pt}\)に対して\(\hspace{2pt}n \leqq x < n+1\hspace{2pt}\)であるとき\(\hspace{2pt}[x]=n\hspace{2pt}\)となります。

\(\hspace{2pt}0 \leqq x \leqq 2\hspace{2pt}\)の範囲において\(\hspace{2pt}[x]\hspace{2pt}\)の値ごとに場合分けすると以下のようになります。

　　[1] \(\hspace{2pt}0 \leqq x < 1\hspace{2pt}\)のとき $$[x]=0 $$ 　　[2] \(\hspace{2pt}1 \leqq x < 2\hspace{2pt}\)のとき $$[x]=1 $$ 　　[3] \(\hspace{2pt} x = 2\hspace{2pt}\)のとき $$[x]=2 $$ となります。
　

[1] \(\hspace{2pt}0 \leqq x < 1\hspace{2pt}\)のとき
　\(\hspace{2pt}[x]=0\hspace{2pt}\)であることから

となります。
　

[2] \(\hspace{2pt}1 \leqq x < 2\hspace{2pt}\)のとき
　\(\hspace{2pt}[x]=1\hspace{2pt}\)であることから

となります。
　

[3] \(\hspace{2pt} x = 2\hspace{2pt}\)のとき
　\(\hspace{2pt}[x]=2\hspace{2pt}\)であることから

となります。
　

以上から、関数\({\hspace{2pt}y=f(x)\hspace{2pt}}\)のグラフは以下の実線となります。
　

【問題(2)の解答】
　問題 : 『関数\(\hspace{2pt}f(x)\hspace{2pt}\)を\(\hspace{2pt}f(x)=(x-[x])^2-2(x-[x])+3-[x]\hspace{2pt}\)とする. ここで\( \hspace{1pt},\hspace{1pt} [x]\hspace{2pt}\)は\(\hspace{2pt}n \leqq x\hspace{2pt}\)を満たす最大の整数\(\hspace{2pt}n\hspace{2pt}\)を表す.
　(1) \(0 \leqq x \leqq 2\hspace{2pt}\)における\(\hspace{2pt}y = f(x)\hspace{2pt}\)のグラフをかけ.
　(2) \(\displaystyle\hspace{2pt}\int_0^2 f(x) \hspace{1pt}dx\hspace{2pt}\)を求めよ.』
　

問題(1)の結果から、定積分\(\displaystyle\hspace{2pt}\int_0^2 f(x) \hspace{1pt}dx\hspace{2pt}\)を求めると

となります。
　

【入試本番に向けたアドバイス】
本問はガウス記号を含んだ定積分を求める問題です。

ガウス記号は教科書の例題ではあまり見かけませんが、入試問題では数学Ⅱの積分に限らずしばしば見かける記号であり、計算に慣れておきましょう。

問題の被積分関数に含まれる\( \hspace{2pt} [x]\hspace{2pt}\)は\(\hspace{2pt}n \leqq x\hspace{2pt}\)を満たす最大の整数\(\hspace{2pt}n\hspace{2pt}\)を表します。

例えば、\([1.6]\hspace{2pt}\)は\(\hspace{2pt}n \leqq 1.6\hspace{2pt}\)を満たす最大の整数であるので $${[1.6] = 1}$$ となります。

また、\([2]\hspace{2pt}\)は\(\hspace{2pt}n \leqq 2\hspace{2pt}\)を満たす最大の整数であるので $${[2] = 2}$$ となります。

一般的には、\(x\hspace{2pt}\)を実数、\(\hspace{1pt}n\hspace{2pt}\)を整数とすると\(\hspace{2pt}n \leqq x < n+1\hspace{2pt}\)であるとき $${[x]=n}$$ となります。

この定義を書き換えると、\([x] \leqq x < [x]+1\hspace{2pt}\)が成り立つことが分かります。
こちらの式も使用することがあるので覚えておきましょう。
　

その他に覚えておくべき性質として、\(n\hspace{2pt}\)を整数としたときに $${[x+n] = [x]+n}$$ が成り立ちます。

例えば、\([2.6]\hspace{2pt}\)に対しては\(\hspace{2pt}[0.6 + 2] = [0.6]+2\hspace{2pt}\)となり、ガウス記号中の実数に対して整数部分を外に出すことができます。
　

ガウス記号を含む問題は一見すると分かりずらいですが、『場合分けしてガウス記号を外す』や『ガウス記号に成り立つ不等式を利用する』などある程度方針が限られます。

問題を何度か解いてガウス記号を含む計算に慣れておくようにしておきましょう。
　

【関連するページ】
・定積分