絶対値付きの積分方程式の問題 | 積分ランダム問題集

【答え】
　$\displaystyle\hspace{1pt}f(x) = 2x-\frac{6}{5}x^2$
　

【解答のポイント】
未知の関数${f(x)}$ が積分に含まれる積分方程式の問題です。

$\displaystyle{ \int_0^1 |f(t)| dt}$ は定数となるため $${\int_0^1 |f(t)| dt = a}$$ と文字に置き換えて積分を計算します。

このとき、被積分関数に絶対値がついていることから、$\hspace{2pt}a > 0\hspace{2pt}$の条件が付きます。

また、定積分の計算では絶対値記号を外すために、定数の値によって場合分けが必要となります。
　

【解答】
　問題 : 『$\displaystyle{f(x) = 2x-2x^2 \int_0^1 |f(t)|dt}$ を満たす関数${\hspace{1pt}f(x)\hspace{2pt}}$を求めよ』
　

$\displaystyle{ \int_0^1 |f(t)|dt}$ は定数となるため $${\int_0^1 |f(t)| dt = a}$$ とおきます。

このとき、関数 ${f(x)}$ は以下のようになります。 $${f(x) = 2x-2ax^2}$$ また、定数$\hspace{1pt}a\hspace{1pt}$は$\hspace{2pt}a > 0\hspace{2pt}$となります。

${\displaystyle \int_0^1 |f(x)| dx \hspace{2pt}}$を求めると

$$ \begin{aligned} & \int_0^1 |f(x)| dx\\[1em] &= \int_0^1 |2x-2ax^2| dx\\[1em] &= 2 \int_0^1 |-x(ax-1)| dx \cdots(1)\\[1em] \end{aligned} $$ となります。

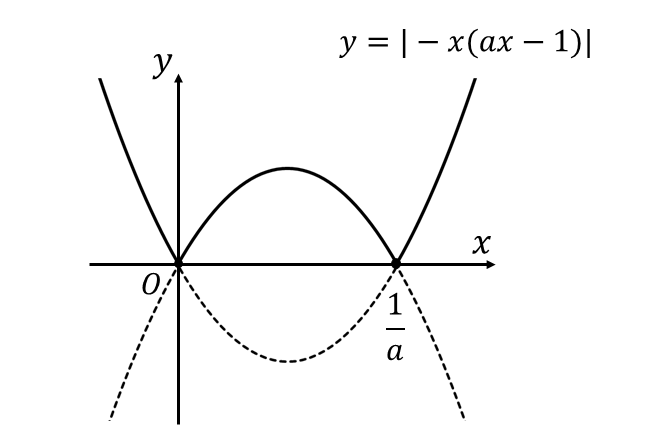
ここで、(1)式の被積分関数$\hspace{2pt}y=|-x(ax-1)|\hspace{2pt}$は以下のようなグラフとなります。絶対値付きの積分方程式
　

上図から、積分区間$\hspace{1pt}[0,1]\hspace{1pt}$に$\displaystyle\hspace{2pt}x = \frac{1}{a}\hspace{2pt}$が含まれるかどうかで以下のように場合分けします。

　[1]$\hspace{2pt} 0 < a < 1\hspace{2pt}$
　[2]$\hspace{2pt} a \geqq 1\hspace{2pt}$
　

　[1]$\hspace{2pt} 0 < a < 1\hspace{2pt}$のとき
(1)式の定積分を計算すると、積分区間$\hspace{1pt}[0,1]\hspace{1pt}$において$\hspace{2pt}-x(ax-1) > 0\hspace{2pt}$となることから

$$ \begin{aligned} \hspace{10pt}& 2 \int_0^1 |-x(ax-1)| dx\\[1em] &= 2 \int_0^1 (-x(ax-1)) dx\\[1em] &= 2 \int_0^1 (-ax^2+x) dx\\[1em] &= 2 \left[- \frac{a}{3}x^3 + \frac{x^2}{2} \right]_0^1 \\[1em] &= 2 \left( -\frac{a}{3} + \frac{1}{2} \right)\\[1em] &= -\frac{2}{3}a +1 \\[1em] \end{aligned} $$

となります。

ここで、$\displaystyle{\int_0^1 |f(t)| dt = a}$ であることから、以下が成り立ちます。 $${-\frac{2}{3}a +1 = a}$$ すなわち $${a = \frac{3}{5} }$$

したがって、求める関数 ${f(x)}$ は $${f(x) = 2x-\frac{6}{5}x^2}$$ となります。
　

　[2]$\hspace{2pt} a \geqq 1\hspace{2pt}$のとき
　　(1)式の定積分を計算すると、積分区間$\hspace{1pt}[0,1]\hspace{1pt}$において
　$\displaystyle\hspace{2pt}0 \leqq x \leqq \frac{1}{a}\hspace{2pt}$のとき$\hspace{2pt}-x(ax-1) \geqq 0$
　$\displaystyle\hspace{2pt} x > \frac{1}{a}\hspace{2pt}$のとき$\hspace{2pt}-x(ax-1) < 0$
となることから

$$ \begin{aligned} \hspace{10pt}& 2 \int_0^1 |-x(ax-1)| dx\\[1em] \hspace{10pt}& = 2 \left\{\int_0^{\frac{1}{a}} (-x(ax-1)) dx + \int_{\frac{1}{a}}^1 x(ax-1) dx \right\}\hspace{10pt} \\[1em] \hspace{10pt}& = 2 \left\{\int_0^{\frac{1}{a}} ( - ax^2+x) dx + \int_{\frac{1}{a}}^1 (ax^2 -x) dx \right\} \hspace{10pt}\\[1em] &= 2 \left\{ \left[- \frac{a}{3}x^3 + \frac{x^2}{2} \right]_0^{\frac{1}{a}} + \left[\frac{a}{3}x^3 -\frac{x^2}{2} \right]_{\frac{1}{a}}^1 \right\}\hspace{10pt}\\[1em] &= 2 \left(\frac{1}{3a^2} + \frac{a}{3} -\frac{1}{2}\right)\\[1em] &= \frac{2}{3a^2} + \frac{2}{3}a -1 \\ \end{aligned} $$

となります。

ここで、$\displaystyle{\int_0^1 |f(t)| dt = a}$ であることから、以下が成り立ちます。 $${\frac{2}{3a^2} + \frac{2}{3}a -1 = a}$$ すなわち $${a^3 + 3a^2 -2 = 0}$$ となります。

ここで、$g(a) = a^3+3a^2 -2\hspace{2pt}$とします。
$\hspace{2pt}g(-1) = 0\hspace{2pt}$であるから、因数定理より$\hspace{2pt}g(a)\hspace{2pt}$は$\hspace{2pt}(a+1)\hspace{2pt}$を因数に持ちます。

$\hspace{2pt}g(a)\hspace{2pt}$は$\hspace{2pt}(a+1)\hspace{2pt}$で割ると$\hspace{2pt}a^2+2a-2\hspace{2pt}$となることから $$ \begin{aligned} & a^3+3a^2 -2\\[0.5em] & = (a+1)(a^2+2a-2)\\ \end{aligned} $$ となります。

解の公式から、$a^2+2a-2 = 0\hspace{2pt}$の解は $${a = -1 \pm \sqrt{3}}$$ となります。

つまり、方程式$\hspace{2pt}a^3 + 3a^2 -2 = 0\hspace{2pt}$は

$${\hspace{10pt}(a+1)(a - (-1+\sqrt{3}))(a - (-1-\sqrt{3}))=0\hspace{10pt}}$$

と因数分解されることから、方程式の解は$\hspace{2pt}a = -1 \hspace{1pt},\hspace{1pt}-1 \pm \sqrt{3} \hspace{2pt}$となります。

これらの値は$\hspace{2pt}a \geqq 1\hspace{2pt}$を満たさないため、不適となります。
　

したがって [1],[2]より求める関数 ${f(x)}$ は $${f(x) = 2x-\frac{6}{5}x^2}$$ となります。
　

【関連するページ】
・定積分
　