maxを用いる定積分

【問題(1)の答え】
\(\hspace{2pt} 0 < a < 1\hspace{2pt}\)のとき
　　\(\displaystyle\hspace{4pt}\frac{a^3}{6} + \frac{1}{3}\hspace{2pt}\)

\(\hspace{2pt} a \geqq 1\hspace{2pt}\)のとき
　　\(\displaystyle\hspace{4pt}\frac{a}{2}\hspace{2pt}\)
　

【問題(2)の答え】
\(\displaystyle\hspace{2pt} 0 < a < \frac{\sqrt{5}-1}{2}\hspace{2pt}\)のとき
　　\(\displaystyle\frac{5 \sqrt{5} -3}{12}\hspace{2pt}\)

\(\displaystyle\hspace{2pt} \frac{\sqrt{5}-1}{2} \leqq a < 1\hspace{2pt}\)のとき
　　\(\displaystyle\frac{a^3}{6} + \frac{1}{2(1+a)}+\frac{1}{3}\hspace{2pt}\)

\(\hspace{2pt} a \geqq 1\hspace{2pt}\)のとき
　　\(\displaystyle\frac{a}{2} + \frac{1}{2(1+a)}\hspace{2pt}\)
　

【解答のポイント】
定積分\(\displaystyle\hspace{2pt}\int_{0}^{1} \max(x^2 , ax) dx\hspace{2pt}\)を求めるためには、まず被積分関数である\(\hspace{2pt}\max(x^2 , ax) \hspace{2pt}\)から\(\hspace{2pt}\max\hspace{2pt}\)の記号を外す必要があります。

そこで、積分区間\(\hspace{1pt}[0,1]\hspace{1pt}\)における\(\hspace{2pt}y=x^2 , y = ax\hspace{2pt}\)のグラフを作り、大小関係を整理します。

まずは、\(\hspace{2pt}y=x^2 , y = ax\hspace{2pt}\)の交点の\(\hspace{2pt}x\hspace{1pt}\)座標を求め、\(a\hspace{2pt}\)の値によって場合分けしてグラフを作ります。

問題(2)は\(\hspace{2pt}3\hspace{1pt}\)つのグラフの大小関係を整理して場合分けする必要があります。
　

【問題(1)の解答】
　問題 :『次の問いに答えよ.ただし、\(a > 0\hspace{2pt}\)とする.
　(1) \(\displaystyle\int_{0}^{1} \max(x^2 , ax) dx\hspace{2pt}\)を求めよ
　(2) \(\displaystyle\int_{0}^{1} \max(x^2 , ax , 1-x) dx\hspace{2pt}\)を求めよ』
　

積分区間\(\hspace{1pt}[0,1]\hspace{1pt}\)において\(\hspace{2pt}y=x^2 \hspace{1pt},\hspace{1pt}y= ax\hspace{2pt}\)のグラフを作ることで大小関係を整理し、\(\max(x^2 , ax)\hspace{2pt}\)の値を求めます。

\(y = x^2\hspace{2pt}\)と\(\hspace{2pt}y = ax\hspace{2pt}\)の交点の\(\hspace{2pt}x\hspace{1pt}\)座標を求めると $$ \begin{aligned} x^2 & = ax \\[0.5em] x(x-a)& = 0 \\[0.5em] \end{aligned} $$ \(a > 0\hspace{2pt}\)であることから、\(x = 0 , a\hspace{2pt}\)に交点を持ちます。

ここで、\(y = x^2\hspace{2pt}\)と\(\hspace{2pt}y = ax\hspace{2pt}\)の上下関係は、\(0 < x < a\hspace{2pt}\)において\(\hspace{2pt}x^2 < ax\hspace{2pt}\)、\( x \geqq a\hspace{2pt}\)において\(\hspace{2pt}x^2 \geqq ax\hspace{2pt}\)となります。

よって、\(x=a\hspace{1pt}\)の値が積分区間\(\hspace{1pt}[0,1]\hspace{1pt}\)に含まれるかどうかで以下のように場合分けをして定積分を求めます。
　[1]\(\hspace{2pt} 0 < a < 1\)
　[2]\(\hspace{2pt} a \geqq 1\)
　

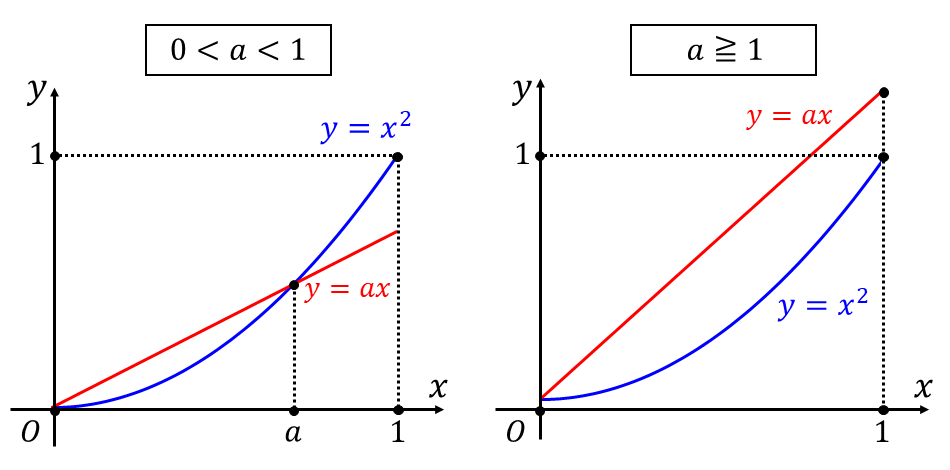
[1] \( 0 < a < 1\hspace{2pt}\)のとき
　\(0 \leqq x \leqq a\hspace{2pt}\)において\(\hspace{2pt}x^2 \leqq ax\hspace{2pt}\)、\( x \geqq a\hspace{2pt}\)において\(\hspace{2pt}x^2 \geqq ax\hspace{2pt}\)であることから問題の定積分は $$ \begin{aligned} & \int_{0}^{1} \max(x^2 , ax) \hspace{1pt}dx \\[1em] &= \int_{0}^{a} ax \hspace{1pt}dx +\int_{a}^{1} x^2 \hspace{1pt}dx \\[1em] &= \left[\frac{a}{2}x^2 \right]_{0}^{a} + \left[\frac{1}{3}x^3 \right]_{a}^{1} \\[1em] &= \frac{a^3}{2} + \frac{1}{3}(1-a^3)\\[1em] &= \frac{a^3}{6} + \frac{1}{3}\\ \end{aligned} $$ となります。
　

[2] \( a \geqq 1\hspace{2pt}\)のとき
　\( 0 \leqq x \leqq 1\hspace{2pt}\)において\(\hspace{2pt}x^2 \leqq ax\hspace{2pt}\)であることから問題の定積分は $$ \begin{aligned} & \int_{0}^{1} \max(x^2 , ax) \hspace{1pt}dx \\[1em] &= \int_{0}^{1} ax \hspace{1pt}dx \\[1em] &= \left[\frac{a}{2}x^2 \right]_{0}^{1} \\[1em] &= \frac{a}{2} \\ \end{aligned} $$ となります。
　

[1],[2]から
\(\hspace{2pt} 0 < a < 1\hspace{2pt}\)のとき\(\displaystyle\hspace{4pt}\frac{a^3}{6} + \frac{1}{3}\hspace{2pt}\)
\(\hspace{2pt} a \geqq 1\hspace{2pt}\)のとき\(\displaystyle\hspace{4pt}\frac{a}{2}\hspace{2pt}\)
と求められます。
　

【問題(2)の解答】
　問題 :『次の問いに答えよ.ただし、\(a > 0\hspace{2pt}\)とする.
　(1) \(\displaystyle\int_{0}^{1} \max(x^2 , ax) dx\hspace{2pt}\)を求めよ
　(2) \(\displaystyle\int_{0}^{1} \max(x^2 , ax , 1-x) dx\hspace{2pt}\)を求めよ』
　

積分区間\(\hspace{1pt}[0,1]\hspace{1pt}\)において\(\hspace{2pt}y=x^2 \hspace{1pt},\hspace{1pt} y=ax \hspace{1pt},\hspace{1pt} y=1-x\hspace{2pt}\)の大小関係を求めることで\(\hspace{2pt}\max(x^2 , ax ,1-x)\hspace{2pt}\)の値を求めて定積分を計算します。

問題(1)から、\(y = x^2\hspace{2pt}\)と\(\hspace{2pt}y = ax\hspace{2pt}\)は\(\hspace{2pt}x=a\hspace{1pt}\)に交点を持ちます。

また、\(y = x^2\hspace{2pt}\)と\(\hspace{2pt}y = 1-x\hspace{2pt}\)の交点の\(\hspace{2pt}x\hspace{1pt}\)座標を求めると $$ \begin{aligned} x^2 & = 1-x \\[0.3em] x^2 + x - 1& = 0 \\ \end{aligned} $$ 解の公式から、\(0 \leqq x \leqq 1\hspace{2pt}\)において\(\displaystyle\hspace{2pt}x = \frac{\sqrt{5}-1}{2}\hspace{2pt}\)に交点を持ちます。

また、\(y = ax\hspace{2pt}\)と\(\hspace{2pt}y = 1-x\hspace{2pt}\)の交点の\(\hspace{2pt}x\hspace{1pt}\)座標を求めると $$ \begin{aligned} ax & = 1-x \\[0.5em] (1+a)x & = 1 \\[0.5em] x & = \frac{1}{1+a} \\ \end{aligned} $$ となります。

ここで、\(x=a\hspace{2pt}\)と\(\displaystyle\hspace{2pt}x = \frac{1}{1+a}\hspace{2pt}\)が一致するときの\(\hspace{2pt}a\hspace{2pt}\)の値は $$ \begin{aligned} a & = \frac{1}{1+a} \\[0.5em] a(1+a) & = 1 \\[0.5em] a^2+a-1 & = 0 \\ \end{aligned} $$ より\(\displaystyle \hspace{2pt}a = \frac{\sqrt{5}-1}{2}\hspace{2pt}\)となります。つまり、\(\displaystyle x=\frac{\sqrt{5}-1}{2}\hspace{2pt}\)において\(\hspace{2pt}3\hspace{2pt}\)つの交点は一致します。

以上から、\(y=x^2 , y=ax , y=1-x\hspace{2pt}\)の上下関係を整理すると、以下の[1],[2],[3]の場合に分けられます。(グラフは後述)

　[1] \(\displaystyle \hspace{2pt}0 < a < \frac{\sqrt{5}-1}{2}\hspace{2pt}\)のとき
　[2] \(\displaystyle \hspace{2pt} \frac{\sqrt{5}-1}{2} \leqq a < 1\hspace{2pt}\)のとき
　[3] \(\hspace{2pt} a > 1\hspace{2pt}\)のとき
　

[1] \(\displaystyle 0 < a < \frac{\sqrt{5}-1}{2}\hspace{2pt}\)のとき
　このとき\(\hspace{2pt} y=x^2 \hspace{1pt},\hspace{1pt} y=ax\hspace{1pt} ,\hspace{1pt} y=1-x\hspace{2pt}\)のグラフは以下のようになります。
　

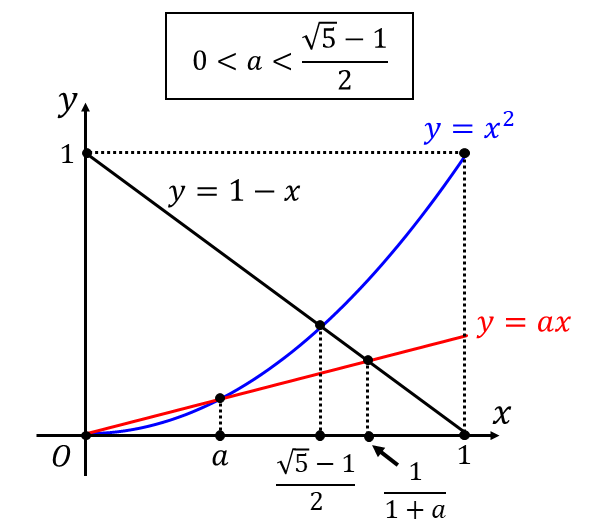
問題の定積分を求めると以下のようになります。(\(\displaystyle\hspace{2pt}\frac{\sqrt{5}-1}{2} = \alpha\hspace{2pt}\)とおきます。) $$ \begin{aligned} & \int_{0}^{1} \max(x^2 , ax , 1-x) \hspace{1pt}dx \\[1em] &= \int_{0}^{\alpha} (1-x) \hspace{1pt}dx + \int_{\alpha}^{1} x^2 \hspace{1pt}dx\\[1em] &= \left[x - \frac{x^2}{2} \right]_{0}^{\alpha} + \left[ \frac{x^3}{3} \right]_{\alpha}^{1} \\[1em] &= \alpha - \frac{\alpha^2}{2} + \frac{1}{3} - \frac{\alpha^3}{3}\\[1em] \end{aligned} $$ となります。

ここで、\(\alpha\hspace{2pt}\)は\(\hspace{2pt}x^2 + x -1 = 0\hspace{2pt}\)の解であるから $$ \begin{aligned} \alpha^2 & = 1- \alpha \\[1em] \alpha^3 & = \alpha \cdot \alpha^2\\[0.5em] &=\alpha(1- \alpha)\\[0.5em] &=-\alpha^2 + \alpha\\[0.5em] & = - (1-\alpha) + \alpha\\[0.5em] & = 2\alpha-1\\ \end{aligned} $$ すなわち $$ \begin{aligned} & \int_{0}^{1} \max(x^2 , ax , 1-x) \hspace{1pt}dx \\[1em] &= \alpha - \frac{\alpha^2}{2} + \frac{1}{3} - \frac{\alpha^3}{3}\\[1em] &= \alpha - \frac{1- \alpha}{2} + \frac{1}{3} - \frac{2\alpha-1}{3}\\[1em] &= \frac{5 \alpha +1}{6}\\[1em] &= \frac{5 \sqrt{5} -3}{12}\\ \end{aligned} $$ となります。
　

[2] \(\displaystyle \frac{\sqrt{5}-1}{2} \leqq a < 1 \hspace{2pt}\)のとき
　このとき\(\hspace{2pt}y=x^2 \hspace{1pt},\hspace{1pt} y=ax \hspace{1pt},\hspace{1pt} y=1-x\hspace{2pt}\)のグラフは以下のようになります。
　

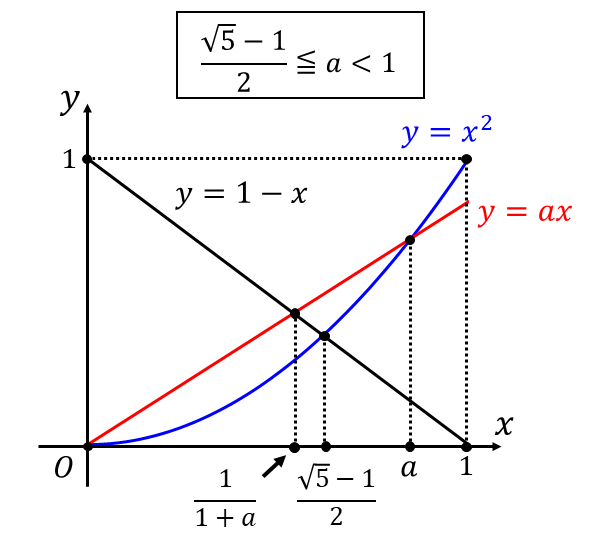
問題の定積分を求めると以下のようになります。

となります。
　

[3] \(\displaystyle a \geqq 1 \hspace{2pt}\)のとき
　このとき\(\hspace{2pt}y=x^2 \hspace{1pt},\hspace{1pt} y=ax \hspace{1pt}, \hspace{1pt}y=1-x\hspace{2pt}\)のグラフは以下のようになります。
　

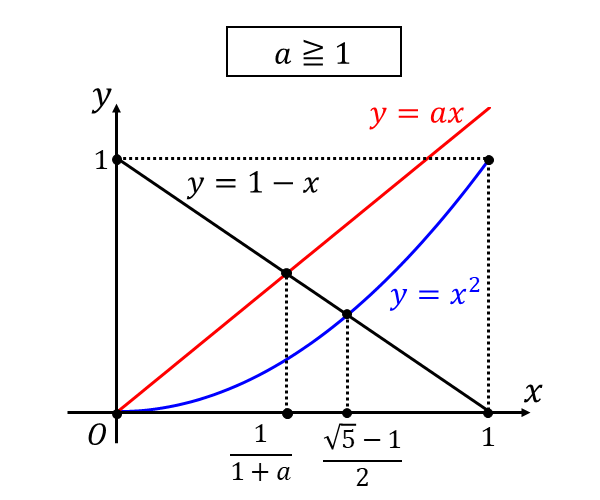
問題の定積分を求めると以下のようになります。

となります。
　

[1],[2],[3]から
\(\displaystyle\hspace{2pt} 0 < a < \frac{\sqrt{5}-1}{2}\hspace{2pt}\)のとき
　　\(\displaystyle\frac{5 \sqrt{5} -3}{12}\hspace{2pt}\)

\(\displaystyle\hspace{2pt} \frac{\sqrt{5}-1}{2} \leqq a < 1\hspace{2pt}\)のとき
　　\(\displaystyle\frac{a^3}{6} + \frac{1}{2(1+a)}+\frac{1}{3}\hspace{2pt}\)

\(\hspace{2pt} a \geqq 1\hspace{2pt}\)のとき
　　\(\displaystyle\frac{a}{2} + \frac{1}{2(1+a)}\hspace{2pt}\)
　

【入試本番に向けたアドバイス】
本問は実数\(\hspace{2pt}\alpha , \beta , \gamma\hspace{2pt}\)に対して最も大きい値を表す\(\hspace{2pt}\max(\alpha , \beta , \gamma)\hspace{2pt}\)を用いた定積分の問題です。

\(\hspace{2pt}\max(\alpha , \beta , \cdots )\hspace{2pt}\)という記号は教科書の例題ではあまり見かけませんが、大学入試ではしばしば出題される記号です。

『\(\hspace{2pt}\max(f(x) , g(x) )\hspace{2pt}\)を含んだ定積分を求める問題』の基本的な方針は以下のような手順となります。
　① \(\hspace{2pt}\max(f(x) , g(x) )\hspace{2pt}\)中の関数\(\hspace{2pt}y=f(x) \hspace{1pt},\hspace{1pt} y=g(x)\hspace{2pt}\)の交点の\(\hspace{2pt}x\hspace{1pt}\)座標を求める
　② \(\hspace{2pt}y=f(x) \hspace{1pt},\hspace{1pt} y=g(x)\hspace{2pt}\)のグラフを描く
　③ 定数の値によって上下関係が変化する場合は、定数によって場合分けする
　④ 定積分を計算する

問題(2)のように3つのグラフの上下関係を調べる場合は少しややこしくなります。

『どのグラフが定数の値によって変わり、どのグラフが固定されているのか』を意識して丁寧にグラフを描き、上下関係を整理しましょう。
　

【関連するページ】
・定積分