絶対値を含む定積分の最小値

【答え】
　\(\displaystyle\hspace{2pt}x = \frac{3}{2}\hspace{2pt}\)のとき最小値\(\hspace{1pt}1\)
　

【解答のポイント】
被積分関数に絶対値記号を含む場合、絶対値を外して積分する必要があります。

絶対値記号は、中身が正か負かで場合分けをすることで外すことができます。 $$|x| = \begin{dcases} x & ( x \geqq 0 ) \\ -x & ( x \lt 0 ) \end{dcases} $$

本問は、被積分関数と積分区間に定数\(\hspace{1pt}x\hspace{1pt}\)が含まれているため、絶対値の外し方が難しく感じます。

そこで、被積分関数の\({\hspace{1pt}f(t)=t-3x+2\hspace{2pt}}\)において\(\hspace{1pt}f(t)=0\hspace{2pt}\)となる\(\hspace{2pt}t\hspace{2pt}\)と積分区間\(\hspace{1pt}[x , x+2]\hspace{1pt}\)との位置関係に着目し、グラフを描くことで場合分けをすると解きやすいです。

\(f(t)=0\hspace{1pt}\)となる\(\hspace{1pt}t\hspace{1pt}\)の値\(\hspace{1pt}t=3x-2\hspace{1pt}\)と積分区間\(\hspace{1pt}[x,x+2]\hspace{1pt}\)の大小関係で場合分けした図を以下に示します。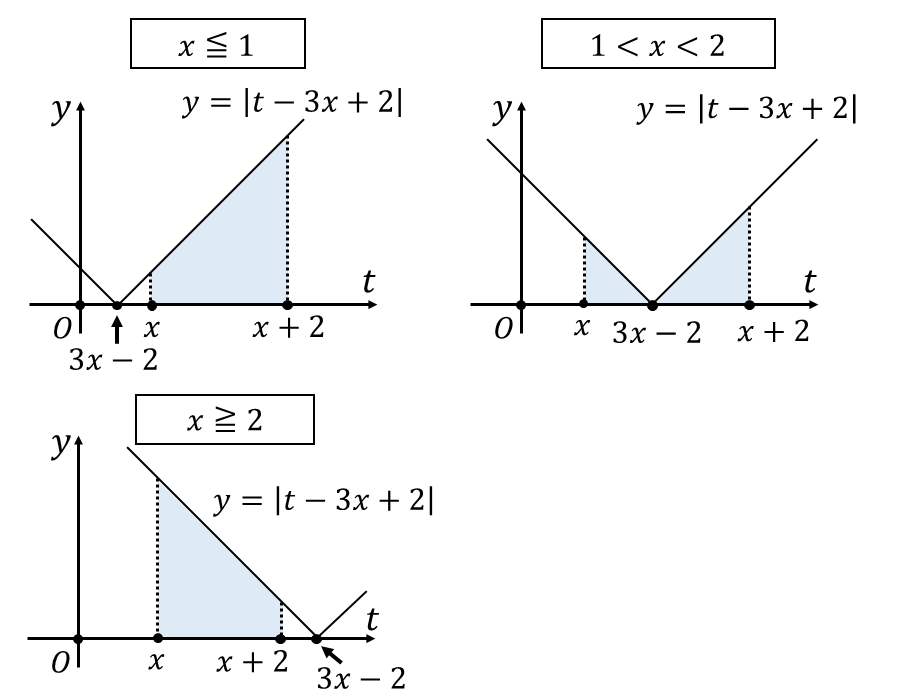
　

【問題の解答】
　問題 :『定積分\(\displaystyle\hspace{2pt}\int_{x}^{x+2} \left | t-3x +2\right |dt\hspace{2pt}\)の最小値とそのときの\(\hspace{1pt}x\hspace{1pt}\)を求めよ』
　

絶対値記号の内側の関数\(\hspace{2pt}f(t) = t-3x +2\hspace{2pt}\)の符号によって場合分けして絶対値記号を外します。

まず、\(f(t)=0\hspace{1pt}\)となる\(\hspace{1pt}t\hspace{1pt}\)の値を求めると $$ \begin{aligned} t-3x +2 & = 0 \\[0.5em] t & = 3x-2 \\[0.5em] \end{aligned} $$ となります。

この\(f(t)=0\hspace{1pt}\)となる\(\hspace{1pt}t\hspace{1pt}\)の値と積分区間\(\hspace{1pt}[x,x+2]\hspace{1pt}\)の大小関係から場合分けをすると、次の[1]～[3]のように場合分けされます。

　[1] \(3x-2 \leqq x\hspace{2pt}\)
　　　すなわち\(\hspace{2pt}x \leqq 1\hspace{2pt}\)のとき

　[2] \(x < 3x-2 < x +2\hspace{2pt}\)
　　　すなわち\(\hspace{2pt}1 < x < 2\hspace{2pt}\)のとき

　[3] \(3x-2 \geqq x+2\hspace{2pt}\)
　　　すなわち\(\hspace{2pt}x \geqq 2\hspace{2pt}\)のとき
　

上記の場合分けを図に表すと、以下のようになります。
　

[1] \(x \leqq 1\hspace{1pt}\)のとき
　\(t-3x +2 \geqq 0\hspace{1pt}\)であることから、定積分は以下のように求められます。 $$ \begin{aligned} & \int_{x}^{x+2} \left | t-3x +2\right |dt \\[0.5em] &= \int_{x}^{x+2} ( t-3x +2) \hspace{1pt}dt \\[0.5em] &= \left[\frac{1}{2}t^2 -3x t + 2t \right]_{x}^{x+2} \\[0.5em] &= -4x+6 \end{aligned} $$ となります。

よって、\(x = 1\hspace{2pt}\)のとき、最小値は\(\hspace{2pt}2\hspace{2pt}\)となります。
　

[2] \(1 < x < 2\hspace{1pt}\)のとき

　\(x < t < 3x-2\hspace{2pt}\)において\(\hspace{1pt}t-3x +2 < 0\hspace{1pt}\)
　\(3x-2 < t < x+2\hspace{2pt}\)において\(\hspace{1pt}t-3x +2 > 0\hspace{1pt}\)
であることから、定積分は以下のように求められます。 $$ \begin{aligned} & \int_{x}^{x+2} \left | t-3x +2\right |dt \\[1em] &= \int_{x}^{3x-2} -( t-3x +2) \hspace{1pt}dt \\[1em] & + \int_{3x-2}^{x+2} ( t-3x +2) \hspace{1pt}dt \\[1em] &= -\left[\frac{1}{2}t^2 -3x t + 2t \right]_{x}^{3x-2} \\[1.5em] &= +\left[\frac{1}{2}t^2 -3x t + 2t \right]_{3x-2}^{x+2} \\[1.5em] &= 4x^2-12x +10 \\ \end{aligned} $$ となります。

上式を平方完成すると $$ \begin{aligned} & 4x^2-12x +10 \\[1em] &= 4 \left( x-\frac{3}{2}\right)^2 +1\\[1em] \end{aligned} $$

よって、\(\displaystyle x = \frac{3}{2}\hspace{2pt}\)のとき、最小値は\(\hspace{2pt}1\hspace{2pt}\)となります。
　

[3] \(x \geqq 2\hspace{1pt}\)のとき
　\(\hspace{1pt}t-3x +2 \leqq 0\hspace{1pt}\)であることから、定積分は以下のように求められます。 $$ \begin{aligned} & \int_{x}^{x+2} \left | t-3x +2\right |dt \\[0.5em] &= \int_{x}^{x+2} -( t-3x +2) \hspace{1pt}dt \\[0.5em] &= -\left[\frac{1}{2}t^2 -3x t + 2t \right]_{x}^{x+2} \\[0.5em] &= 4x-6 \end{aligned} $$ となります。

よって、\(x = 2\hspace{2pt}\)のとき、最小値は\(\hspace{2pt}2\hspace{2pt}\)となります。
　

[1],[2],[3]から\(\displaystyle\hspace{2pt}x = \frac{3}{2}\hspace{2pt}\)のとき最小値\(\hspace{1pt}1\hspace{1pt}\)となります。
　

【入試本番に向けたアドバイス】
本問は定数\(\hspace{1pt}x\hspace{1pt}\)を含んだ絶対値付きの定積分 $${\int_{x}^{x+2} \left | t-3x +2\right |dt}$$ を求めた後、\(x\hspace{1pt}\)を変数とみなして定積分の最小値を求める問題です。

このように『定数を含んだ絶対値付きの定積分の最小値・最大値を求める問題』は、数学Ⅱの入試問題で非常に出題頻度の高いパターンのため、必ず解けるようにしておきましょう。

定積分の最小値・最大値を求める問題の基本的な方針は以下のような手順となります。
　① 被積分関数のグラフを描く
　② 必要であれば、定数によって場合分けする
　③ 絶対値記号を外して積分する
　④ \(f(a) = \cdots \hspace{2pt}\)とおいて\(\hspace{1pt}f(a)\hspace{1pt}\)の増減表を作る
　(本問は定積分の結果が二次以下の関数となるため、平方完成から求めています。)

特に、本問は被積分関数と積分区間のどちらも\(\hspace{2pt}x\hspace{2pt}\)が含まれていることから、やや難しい問題となっています。

絶対値記号を外すときに『\(\hspace{2pt}f(t) = 0\hspace{2pt}\)となる\(\hspace{2pt}t\hspace{2pt}\)を求め、積分区間\(\hspace{1pt}[x,x+2]\hspace{1pt}\)との大小関係で場合分けする』という方針を覚えておくと迷わず計算を進めることができます。
　

【関連するページ】
・定積分