-光と光学に関連する用語の解説サイト-

減衰曲線e^(-x)sinxの面積

◆第問目！

【 数Ⅲ : 難易度 ★★★ 】
　\(k\hspace{1pt}\)を\(\hspace{1pt}0\hspace{1pt}\)以上の整数とする。\(\hspace{2pt}k\pi \leqq x \leqq (k+1)\pi\hspace{2pt}\)において曲線\({\hspace{1pt} y=e^{-x}\sin x\hspace{2pt}}\)と\(\hspace{2pt}x\hspace{2pt}\)軸に囲まれる面積\(\hspace{1pt}S(k)\hspace{1pt}\)とするとき、以下の問いに答えよ。
　(1) 不定積分\(\displaystyle{\hspace{2pt}\int e^{-x} \sin x\hspace{1pt}dx}\) を求めよ
　(2) \(\hspace{2pt} S(k) \hspace{2pt}\)を求めよ
　(3) \(\displaystyle \hspace{2pt} \sum_{k=0}^\infty S(k)\hspace{2pt}\)を求めよ

\(\displaystyle{\int e^{-x} \sin x\hspace{1pt}dx}\) は部分積分を\(\hspace{1pt}2\hspace{1pt}\)回繰り返すことで値を求めることができます。

問題の曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\)は、以下のように\({\hspace{1pt}x\hspace{2pt}}\)軸を中心に振動し、\({x\hspace{2pt}}\)が大きいほどその振動の振れ幅が小さくなるグラフとなります。
減衰曲線e^(-x)sinxのグラフの概形

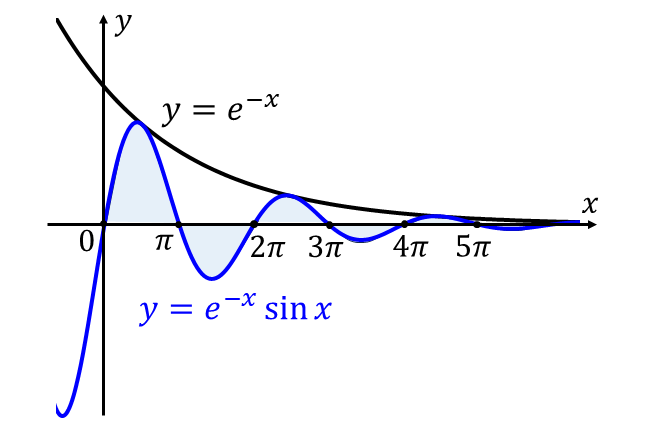
\(k\hspace{1pt}\)を\(\hspace{1pt}0\hspace{1pt}\)以上の整数とするとき、\(k\pi \leqq x \leqq (k+1)\pi\hspace{2pt}\)において曲線\({\hspace{1pt} y=e^{-x}\sin x\hspace{2pt}}\)と\(\hspace{2pt}x\hspace{2pt}\)軸に囲まれる面積とは、上図の\(\hspace{2pt}x\hspace{1pt}\)軸との交点により区切られた山一つ分の面積となります。

\(k\pi \leqq x \leqq (k+1)\pi\hspace{2pt}\)における面積は、定積分を用いて以下のように表されます。 $${\int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx}$$

初項\(\hspace{1pt}a\hspace{2pt}\)、公比\(\hspace{1pt}r\hspace{2pt}\)の無限等比級数において\(\hspace{2pt}|r|< 1 \hspace{2pt}\)のとき、その無限等比級数の和は収束し、その値は $${\sum_0^\infty S(k) = \frac{a}{1-r}}$$ となります。

【答え】
　(1) \(\displaystyle -\frac{e^{-x}}{2}(\sin x + \cos x)+C \) (\(\hspace{2pt}C\hspace{1pt}\)は積分定数)

　(2) \(\displaystyle \frac{e^{-\pi}+1}{2} e^{-k \pi} \)

　(3) \(\displaystyle \frac{e^{\pi}+1}{2(e^{\pi}-1)} \)
　

【解答のポイント】
曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\) は減衰曲線といい、以下のように\({\hspace{1pt}x\hspace{2pt}}\)軸を中心に振動し、\({x\hspace{2pt}}\)が大きいほどその振動の振れ幅が小さくなるグラフとなります。
(以下のグラフは振動の様子が見やすいように加工しているため厳密ではありません) 減衰曲線e^(-x)sinxに囲まれた面積を求める問題

問題(2)の曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\)と\({\hspace{1pt}x\hspace{2pt}}\)軸に囲まれた\(k\pi \leqq x \leqq (k+1)\pi\hspace{2pt}\)における面積\(\hspace{1pt}S(k)\hspace{2pt}\)とは、上図の\(\hspace{2pt}x\hspace{1pt}\)軸との交点により区切られた山一つ分の面積となります。

また、問題(3)の\(\displaystyle \hspace{2pt} \sum_{k=0}^\infty S(k)\hspace{2pt}\)とは、上図の\(\hspace{1pt}x \geqq 0\hspace{1pt}\)におけるすべての山の面積の和(青く塗られた領域)となります。

\(S(k)\hspace{2pt}\)を定積分により表すと $${S(k) =\int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx}$$ と表されます。

本問は、この定積分の計算方法がポイントとなります。
地道に計算する方法では、\({k \pi \leqq x \leqq (k+1)\pi \hspace{2pt}}\)において被積分関数の符号が一定であることから

$$ \begin{aligned} \hspace{10pt} & \int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx \\[1em] &= \left|\int_{k \pi}^{(k+1) \pi} e^{-x} \sin x\hspace{1pt}dx \right|\hspace{10pt} \\[1em] \end{aligned} $$

と変形して、絶対値記号の中身の定積分を計算します。

この方法では特別なテクニックは必要ありませんが、やや定積分の計算に時間がかかります。

一方、別解として記載していますが、変数を\(\hspace{1pt}x - k\pi = t\hspace{2pt}\)と置き換える方法もあります。
この方法は知識として覚えておく必要がありますが、定積分の計算を大幅に省くことができます。
　

【問題(1)の解答】
　問題 :『不定積分\(\displaystyle{\hspace{2pt}\int e^{-x} \sin x\hspace{1pt}dx}\) を求めよ』
　

\(\displaystyle{I=\int e^{-x} \sin x\hspace{1pt}dx}\) とおき、部分積分から以下のように求めます。

$$ \begin{aligned} \hspace{10pt}I & = \int e^{-x} \sin x \hspace{1pt}dx \\[1em] &= \int (-e^{-x})' \sin x \hspace{1pt}dx \\[1em] &= -e^{-x} \sin x - \int (-e^{-x}) \cos x \hspace{1pt}dx\\[1em] &= -e^{-x} \sin x + \int e^{-x} \cos x \hspace{1pt}dx\\[1em] \end{aligned} $$

ここで、\({ \int e^{-x} \cos x \hspace{1pt}dx\hspace{1pt}\hspace{2pt}}\)をさらに部分積分を用いて計算すると

$$ \begin{aligned} \hspace{10pt}& \int e^{-x} \cos x \hspace{1pt}dx \\[1em] &= \int (-e^{-x})' \cos x \hspace{1pt}dx \\[1em] &= -e^{-x} \cos x - \int (-e^{-x}) (-\sin x) \hspace{1pt}dx\\[1em] &= -e^{-x} \cos x - \int e^{-x} \sin x \hspace{1pt}dx\\[1em] &= -e^{-x} \cos x - I\\[1em] \end{aligned} $$

となります。

したがって $${I = -e^{-x} \sin x -e^{-x} \cos x - I}$$ となることから $${I = -\frac{e^{-x}}{2}(\sin x + \cos x)+C}$$ (\(\hspace{2pt}C\hspace{2pt}\)は積分定数) と求められます。
　

【問題(2)の解答】
　問題 :『\(k\hspace{1pt}\)を\(\hspace{1pt}0\hspace{1pt}\)以上の整数とする。\(\hspace{2pt}k\pi \leqq x \leqq (k+1)\pi\hspace{2pt}\)において曲線\({\hspace{1pt} y=e^{-x}\sin x\hspace{2pt}}\)と\(\hspace{2pt}x\hspace{2pt}\)軸に囲まれる面積\(\hspace{1pt}S(k)\hspace{1pt}\)とする。面積\(\hspace{1pt} S(k) \hspace{2pt}\)を求めよ』
　

\({y=e^{-x}\sin x\hspace{2pt}}\)と\({\hspace{1pt}x\hspace{2pt}}\)軸との交点は、\({x \geqq 0\hspace{1pt}}\)において\({\hspace{1pt}\sin x = 0\hspace{2pt}}\)となる点であるため、\({x=k \pi\hspace{2pt}}\)(\({\hspace{1pt}k\hspace{2pt}}\)は\({\hspace{1pt}0\hspace{2pt}}\)以上の整数)となります。

\(\hspace{2pt}k\pi \leqq x \leqq (k+1)\pi\hspace{2pt}\)における面積\(\hspace{1pt}S(k)\hspace{1pt}\)は以下のように表されます。 $${S(k) =\int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx}$$

\({k \pi \leqq x \leqq (k+1)\pi \hspace{2pt}}\)において被積分関数の符号が一定なので

$$ \begin{aligned} \hspace{10pt} & \int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx \\[1em] &= \left|\int_{k \pi}^{(k+1) \pi} e^{-x} \sin x\hspace{1pt}dx \right|\hspace{10pt} \\[1em] \end{aligned} $$

となります。

\(\displaystyle{S(k)=\left|\int_{ k \pi}^{(k+1) \pi} e^{-x} \sin x\hspace{1pt}dx \right|}\) を求めると、問題(1)の結果から

$$ \begin{aligned} \hspace{15pt}S(k)= & \left|\int_{ k \pi}^{ (k+1) \pi} e^{-x} \sin x\hspace{1pt}dx \right|\\[1em] &= \left| \left[ -\frac{1}{2}e^{-x}(\sin x + \cos x) \right]_{k \pi}^{(k+1) \pi} \right|\hspace{10pt} \\[1em] &= \left| -\frac{1}{2} \left(e^{-(k+1)\pi}\left(\sin (k+1)\pi + \cos (k+1)\pi \right) - e^{-k\pi}\left(\sin k\pi + \cos k\pi \right)\right)\right|\hspace{10pt} \\[1em] &= \left| -\frac{1}{2} \left(e^{-(k+1)\pi}(-1)^{k+1} - e^{-k\pi}(-1)^{k}\right)\right| \\[1em] &=\frac{1}{2} \left(e^{-(k+1)\pi} + e^{-k\pi}\right)\\[1em] &=\frac{e^{-\pi}+1}{2} e^{-k \pi} \\[1em] \end{aligned} $$

(上記の計算では \({\sin k \pi=0\hspace{2pt},\hspace{2pt}\cos k \pi=(-1)^k}\) から式変形しています。)
　

【問題(2)の別解】
上記の解法では、\(\displaystyle{\left|\int_{ k \pi}^{(k+1) \pi} e^{-x} \sin x\hspace{1pt}dx \right|}\) をそのまま計算しましたが、変数を\(\hspace{1pt}x - k\pi = t\hspace{2pt}\)と置き換えることで定積分の計算を省略して求めることもできます。

\(\hspace{1pt}e^{-x} > 0\hspace{2pt}\)であることから

$$ \begin{aligned} \hspace{10pt} & \int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx \\[1em] &= \int_{k \pi}^{(k+1) \pi} e^{-x} |\sin x|\hspace{1pt}dx \hspace{10pt} \\[1em] \end{aligned} $$

ここで、\(x - k\pi = t\hspace{1pt}\)と置き換えます。

変数\({\hspace{1pt}x\hspace{2pt}}\)の範囲に対応する変数\({\hspace{1pt}t\hspace{2pt}}\)の範囲を求めると、以下のようになります。

\({x}\) \({\displaystyle k \pi \to (k+1)\pi}\)
\({t}\) \(\displaystyle{0 \to \pi}\)

また、\(x = t + k\pi\hspace{1pt}\)の両辺を\(\hspace{1pt}t\hspace{1pt}\)について微分すると\(\displaystyle\hspace{1pt} \frac{dx}{dt} = 1\hspace{2pt}\)となることから\(\hspace{2pt}dx = dt\hspace{2pt}\)と表されます。

すなわち

$$ \begin{aligned} \hspace{10pt}S(k) = & \int_{\pi k}^{\pi (k+1)} e^{-x}| \sin x |\hspace{1pt}dx\\[1em] &= \int_{0}^{\pi} e^{-t-k\pi}| \sin (t+k\pi) |\hspace{1pt}dt \hspace{10pt}\\[1em] &= \int_{0}^{\pi} e^{-t-k\pi}| (-1)^k \sin t |\hspace{1pt}dt \\[1em] &= \int_{0}^{\pi} e^{-t-k\pi}| \sin t |\hspace{1pt}dt \\[1em] &= e^{-k\pi} \int_{0}^{\pi} e^{-t} \sin t \hspace{1pt}dt \\[1em] \end{aligned} $$

となります。(上式において、\(0 \leqq t \leqq \pi\hspace{2pt}\)で\(\hspace{2pt}\sin t \geqq 0 \hspace{2pt}\)であることから\(\hspace{2pt} |\sin t| = \sin t\hspace{2pt}\)としています。)

問題(1)から、\(\displaystyle \int_0^\pi e^{-x} \sin x\hspace{1pt}dx =\frac{e^{-\pi}+1}{2} \hspace{2pt}\)であることから

$$ \begin{aligned} \hspace{10pt}S(k) = & e^{-k\pi} \int_{0}^{\pi} e^{-t} \sin t \hspace{1pt}dt\\[1em] &= \frac{e^{-\pi}+1}{2} e^{-k \pi} \\[1em] \end{aligned} $$

となります。
　

【問題(3)の解答】
　問題 :『\(\displaystyle \hspace{2pt} \sum_{k=0}^\infty S(k)\hspace{2pt}\)を求めよ』
　

\(\displaystyle \hspace{2pt} \sum_{k=0}^\infty S_k\hspace{2pt}\)を求めると

$$ \begin{aligned} \hspace{10pt} \sum_{k=0}^\infty S_k & = \sum_{k=0}^\infty \frac{e^{-\pi}+1}{2} e^{-k \pi}\\[1em] &= \frac{e^{-\pi}+1}{2} \sum_{k=0}^\infty e^{-k \pi}\\[1em] \end{aligned} $$

ここで、\(\displaystyle{\hspace{1pt}\sum_{k=0}^\infty e^{-k \pi}\hspace{2pt}}\)は初項\({\hspace{1pt}1\hspace{2pt}}\)、公比\({\hspace{1pt}e^{-\pi}\hspace{2pt}}\)の無限等比級数であり、\({\hspace{1pt}0 < e^{-\pi} < 1\hspace{2pt}}\)より収束することから $$ \begin{aligned} \hspace{10pt}\sum_{k=0}^\infty S_k & = \frac{e^{-\pi}+1}{2} \sum_{k=0}^\infty e^{-k \pi}\\[1em] &= \frac{e^{-\pi}+1}{2} \times \frac{1}{1-e^{-\pi}}\hspace{10pt}\\[1em] &= \frac{e^{\pi}+1}{2(e^{\pi}-1)}\\[1em] \end{aligned} $$ と求められます。
　

【入試本番に向けたアドバイス】
本問は、曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\)と\({\hspace{1pt}x\hspace{2pt}}\)軸に囲まれた面積を求める問題です。

『\({\hspace{1pt}\int e^{-x}\sin x\hspace{2pt}dx\hspace{1pt}}\)の積分』『絶対値記号の扱い方』『無限等比級数』など総合的な知識を必要とする問題であり、入試問題で頻出の問題でもあるため、何度も解いて解法を頭に入れておきましょう。
　

・減衰曲線の特徴
本問の減衰曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\)は入試問題では頻出であり、グラフの特徴を覚えておくと他の問題でも役に立ちます。

先述のように、減衰曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\)は以下のようなグラフとなります。 減衰曲線e^(-x)sinxの特徴

減衰曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\)の特徴として、以下のような点があります。
　・\({\hspace{1pt}x\hspace{2pt}}\)軸との交点は\(\hspace{1pt}x = n\pi\hspace{1pt}\)(\(n\hspace{1pt}\)は整数)
　・\({\hspace{1pt}x\hspace{2pt}}\)軸を中心に振動する
　・\({\hspace{1pt}x\hspace{2pt}}\)が大きいほど、振動の振れ幅は\(\hspace{2pt}y=\pm e^{-x}\hspace{2pt}\)に挟まれて小さくなる
　・減衰曲線の極大値の和は、無限等比級数の和となる
　・減衰曲線と\(\hspace{1pt}x\hspace{1pt}\)軸に囲まれた面積は、無限等比級数の和となる

『減衰曲線の極大値の和が無限等比級数の和となる』ことは本問には出てきませんでしたが、数Ⅲの微分の範囲ではよく出題される問題のため、一緒に覚えておきましょう。
　

【関連するページ】
・定積分

【出題範囲】　　【難易度】



　




　【問題の種類を絞る】



Copyright (c) 光学技術の基礎用語 All Rights Reserved.