対数関数とx軸に囲まれた面積

【答え】
　(1) \(\displaystyle x\log x -x + C \) (\(\hspace{2pt}C\hspace{2pt}\)は積分定数)

　(2) \(\displaystyle S(a)= 2e^a -3a -3 + 2\log 2 \)

　(3) \(\hspace{2pt}a=\log \frac{3}{2}\hspace{2pt}\)のとき、最小値\(\displaystyle\hspace{2pt}5\log 2 -3\log 3\)
　

【解答のポイント】
曲線\(\hspace{2pt}y=f(x) \hspace{1pt}, \hspace{1pt} x \hspace{2pt}\)軸\(\hspace{2pt},\hspace{2pt}x=x_1 \hspace{1pt}, \hspace{1pt}x=x_2\hspace{2pt}\)に囲まれた面積は $${ \int_{x_1}^{x_2} |f(x)|\hspace{1pt}dx}$$ と表されます。

本問で求める面積は\(\hspace{2pt}f(x) = \log x -a\hspace{2pt} \) \(\hspace{2pt},\hspace{2pt}x_1=1 \hspace{1pt}, \hspace{1pt}x_2 = 2\hspace{2pt}\)とすればよいので $${ \int_1^2 |\log x -a|\hspace{1pt}dx}$$ となります。

被積分関数に絶対値記号が含まれる場合は、符号を調べて絶対値記号を外す必要があります。

まず、\( \log x - a=0\hspace{2pt}\)となる\(\hspace{1pt}x\hspace{1pt}\)の値を求めることで\(\hspace{2pt}x\hspace{1pt}\)軸との交点の座標を求めます。

次に、\(y=\log x -a\hspace{2pt}\)のグラフを描くことで符号を調べます。
(本問は簡単な\(\hspace{2pt}\log x\hspace{2pt}\)の関数であるため、グラフは省略しても問題ありません。)
　

【問題(1)の解答】
　問題 :『不定積分 \(\displaystyle \int \log x\hspace{2pt}\)を求めよ』
　

部分積分

$$ \begin{aligned} & \int f'(x)\hspace{1pt} g(x)\hspace{1pt}dx \\ &\hspace{2pt}= f(x)\hspace{1pt}g(x)- \int f(x)\hspace{1pt}g'(x)\hspace{1pt}dx \\ \end{aligned} $$ から計算します。

\({f'(x)=1\hspace{2pt},\hspace{1pt}g(x)=\log x}\) とすると、以下のように求められます。

【問題(2)の解答】
　問題 :『曲線\(\hspace{2pt} y=\log x -a\hspace{2pt},\)\({\hspace{2pt}x\hspace{1pt}}\)軸\(\hspace{2pt},\hspace{2pt}x=1\hspace{2pt},\)\(\hspace{2pt}x=2\hspace{2pt}\)により囲まれた面積\(\hspace{1pt}S(a)\hspace{1pt}\)を求めよ。ただし\(\hspace{2pt}a\hspace{2pt}\)は\(\hspace{2pt}0 \leqq a \leqq \log 2\hspace{2pt}\)とする。』
　

曲線\(\hspace{2pt} y=\log x -a\hspace{2pt},\)\({\hspace{2pt}x\hspace{1pt}}\)軸\(\hspace{2pt},\hspace{2pt}x=1\hspace{2pt},\)\(\hspace{2pt}x=2\hspace{2pt}\)により囲まれた面積\(\hspace{1pt}S(a)\hspace{1pt}\)は $${S(a) = \int_1^2 |\log x - a|\hspace{1pt}dx}$$ となります。

被積分関数に絶対値記号を含んでいるため、\(f(x) = \log x - a\hspace{2pt}\)の符号を調べて絶対値記号を外します。

まず、\(f(x)=0\hspace{2pt}\)となる\(\hspace{1pt}x\hspace{1pt}\)の値を求めると $$ \begin{aligned} \hspace{10pt}\log x - a &= 0 \\[1em] \log x &= a \\[1em] x &= e^a \\[1em] \end{aligned} $$

となります。

ここで、\(\hspace{2pt}a\hspace{2pt}\)は\(\hspace{2pt}0 \leqq a \leqq \log 2\hspace{2pt}\)であることから $${e^0 \leqq e^a \leqq e^{\log 2}}$$ すなわち $${1 \leqq e^a \leqq 2}$$ となります。

(\(\hspace{2pt}e^{\log 2} = p\hspace{2pt}\)とおくと、両辺に\(\hspace{2pt}\log\hspace{2pt}\)をとり\(\hspace{2pt}\log e^{\log 2} = \log p\hspace{2pt}\)すなわち\(\hspace{2pt}\log 2 = \log p\hspace{2pt}\)から\(\hspace{1pt}p=2\hspace{1pt}\)となります。)

曲線\(\hspace{2pt} y=\log x -a\hspace{2pt},\)\({\hspace{2pt}x\hspace{1pt}}\)軸\(\hspace{2pt},\hspace{2pt}x=1\hspace{2pt},\)\(\hspace{2pt}x=2\hspace{2pt}\)により囲まれた面積\(\hspace{1pt}S(a)\hspace{1pt}\)を図示すると、以下のようになります。

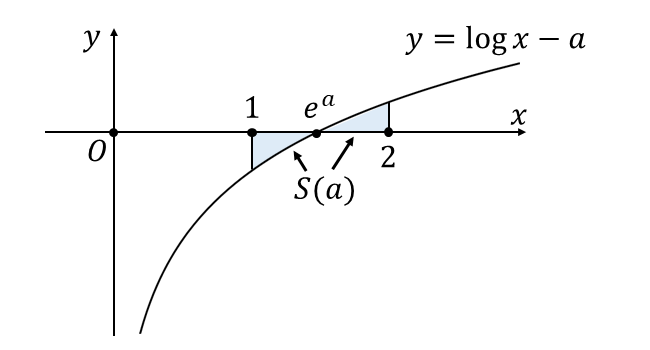
よって、上図から絶対値記号を外して定積分を計算すると、以下のようになります。

【問題(3)の解答】
　問題 :『面積\(\hspace{1pt}S(a)\hspace{2pt}\)の最小値と、そのときの\(\hspace{1pt}a\hspace{1pt}\)の値を求めよ』
　

\(\displaystyle\hspace{2pt}S(a) = 2e^a -3a -3 + 2\log 2\hspace{2pt}\)を微分すると $${S'(a) = 2e^a -3}$$ となります。

上式から\(\hspace{2pt}S'(a)=0\hspace{2pt}\)を満たす\(\hspace{2pt}a\hspace{2pt}\)を求めると $$ \begin{aligned} 2e^a -3 & =0 \\[1em] e^a & = \frac{3}{2} \\[1em] a & =\log \frac{3}{2} \\[1em] \end{aligned} $$ となります。

\( a < \log \frac{3}{2} \hspace{2pt}\)のとき\(\hspace{2pt}S'(a) < 0 \hspace{2pt}\)、\(a > \log \frac{3}{2}\hspace{2pt}\)のとき\(\hspace{2pt}S'(a) > 0 \hspace{2pt}\)であることから、\(S(a)\hspace{2pt}\)は\(\hspace{2pt}x=\log \frac{3}{2}\hspace{2pt}\)で極小値となります。

\( S \left(\log \frac{3}{2} \right)\hspace{2pt}\)の値を求めると

となります。

( \(\hspace{2pt}e^{\log \frac{3}{2}}\hspace{2pt}\)の値は、\(p = e^{\log \frac{3}{2}}\hspace{2pt}\)としたときに両辺に\(\hspace{2pt}\log \hspace{2pt}\)をとると\(\hspace{2pt}\log p = \log \frac{3}{2}\hspace{2pt}\)となることから\(\hspace{2pt}p=\frac{3}{2}\hspace{2pt}\)より求められます。)

すなわち、\(S(a)\hspace{2pt}\)の増減表は以下のようになります。

したがって、面積\(\hspace{2pt}S(a)\hspace{2pt}\)は\(\hspace{2pt}a=\log \frac{3}{2}\hspace{2pt}\)のとき、最小値\(\displaystyle\hspace{2pt}5\log 2 -3\log 3\hspace{1pt}\)となります。
　

【関連するページ】
・定積分

・部分積分