陰関数(2x^2 -2xy + y^2=3)に囲まれた面積

【答え】
　\(\displaystyle 3 \pi \)
　

【解答のポイント】
陰関数の面積を求める問題は、まず関数を変形して\({\hspace{1pt}y=\cdots\hspace{2pt}}\)の形に変形します。

次に得られた式を連立させて、グラフの交点を求めます。

最後に、囲まれる範囲において (上側の関数)-(下側の関数) の式を作り、定積分から面積を求めます。
　

【解答】
　問題 : 『 \({2x^2 -2xy + y^2=3\hspace{2pt}}\)に囲まれる面積を求めよ』
　

まず関数を変形して\({\hspace{1pt}y=\cdots\hspace{2pt}}\)の形に変形します。

$$ \begin{aligned} \hspace{10pt}& 2x^2 -2xy + y^2=3 \\[0.5em] & y^2-2xy + 2x^2 -3 = 0\\[0.5em] \end{aligned} $$

解の公式から $$ \begin{aligned} \hspace{10pt} y &= x \pm \sqrt{x^2 -(2x^2-3)} \\[0.5em] & = x \pm \sqrt{3-x^2} \\[0.5em] \end{aligned} $$

と変形することができます。

上式から、\(x\hspace{1pt}\)の定義域は\({\hspace{2pt}-\sqrt{3} \leqq x \leqq \sqrt{3}\hspace{2pt}}\)となります。

ここで、以下の二式を連立させて交点を求めます。 $$ \begin{aligned} y &= x + \sqrt{3-x^2} \hspace{10pt}\cdots(1) \\[0.5em] y &= x - \sqrt{3-x^2} \hspace{10pt}\cdots(2) \\[0.5em] \end{aligned} $$

(1)式と(2)式から\({\hspace{1pt}y\hspace{2pt}}\)を削除すると

すなわち、交点の\({\hspace{1pt}x\hspace{2pt}}\)座標は\({\hspace{1pt}-\sqrt{3}\hspace{1pt},\hspace{1pt}\sqrt{3}\hspace{2pt}}\)となります。

また、\({-\sqrt{3} \leqq x \leqq \sqrt{3}\hspace{2pt}}\)の範囲において、\({\hspace{1pt}x + \sqrt{3-x^2} \geqq x - \sqrt{3-x^2} \hspace{2pt}}\)となります。

よって、求める面積は以下のようになります。

ここで、\(\displaystyle{\hspace{1pt}\int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{3-x^2} \hspace{1pt}dx\hspace{2pt}}\)は半径\({\hspace{1pt}\sqrt{3}\hspace{2pt}}\)の円の2分の1の面積を表すため

と求められます。
　

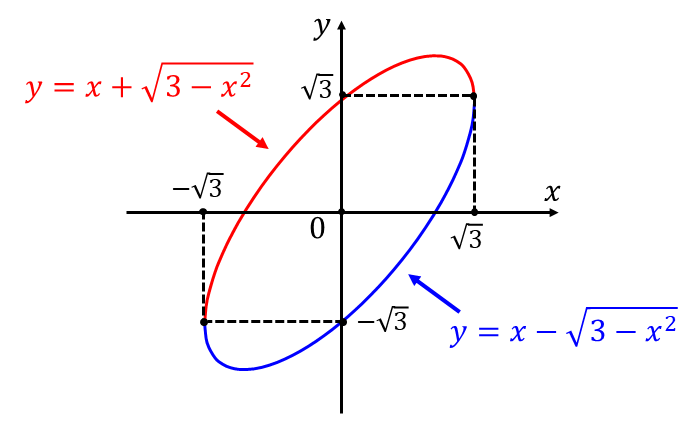
参考として問題の陰関数のグラフは以下のようになります。本問では、積分区間と上下関係がすぐに分かるためグラフを描く必要はありません。