-光と光学に関連する用語の解説サイト-

二次関数と直線に囲まれた部分の面積

◆第問目！

【 数Ⅱ : 難易度 ★★★ 】
　曲線\(\hspace{1pt}y = |x^2-4x|\hspace{2pt}\)と直線\(\hspace{2pt}y = ax\hspace{2pt}\)が異なる\(\hspace{1pt}3\hspace{1pt}\)点を共有している。この曲線と直線に囲まれた面積を\(\hspace{1pt}S\hspace{1pt}\)とする。ただし、\(a\hspace{1pt}\)は実数とする。
　(1) \(a \hspace{2pt}\)の範囲を求めよ
　(2) 面積\(\hspace{1pt}S \hspace{2pt}\)を\(\hspace{1pt}a\hspace{1pt}\)により表せ
　(3) 面積\(\hspace{1pt}S\hspace{1pt}\)が最小値となる\(\hspace{2pt}a\hspace{2pt}\)を求めよ

まずは、関数\(\hspace{1pt}y = |x^2 -4x|\hspace{1pt}\)のグラフを描いて、曲線と直線が異なる\(\hspace{1pt}3\hspace{1pt}\)点を共有するための条件を考えます。

グラフを参考にして、直線の傾きから\(\hspace{1pt}3\hspace{1pt}\)点を共有する条件を考えると素早く条件を求められます。

直線と二次関数に囲まれた部分の面積は1/6公式

$${\hspace{10pt}\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3 \hspace{10pt}}$$

を使用すると簡単に計算ができます。

1/6公式から計算できる面積を足し引きすることで、面積を素早く求めることができます。

問題(1)と(2)から、\(\displaystyle\hspace{2pt}0 < a < 4\hspace{2pt}\)の範囲で面積\(\displaystyle\hspace{1pt}S(a) \hspace{2pt}\)の増減表を作ることで最小値となる\(\hspace{1pt}a\hspace{1pt}\)の値を求めます。

【答え】
　(1) \(\hspace{1pt}0 < a < 4\hspace{1pt}\)

　(2) \(\displaystyle\hspace{1pt}S = -\frac{1}{6}a^3 + 6a^2 -8a + \frac{32}{3}\hspace{1pt}\)

　(3) \(\hspace{1pt}a = 12 - 8\sqrt{2}\hspace{1pt}\)
　

【解答のポイント】
絶対値記号は、中身が正か負かで場合分けをすることで外すことができます。 $$|x| = \begin{dcases} x & ( x \geqq 0 ) \\ -x & ( x \lt 0 ) \end{dcases} $$

関数\(\hspace{1pt}y = |x^2 -4x|\hspace{2pt}\)は\(\hspace{1pt}x\hspace{1pt}\)の範囲によって
　[1] \(x \leqq 0\hspace{2pt}\)または\(\hspace{2pt}x \geqq 4\hspace{2pt}\)のとき
　[2] \(0 < x < 4\hspace{1pt}\)のとき
で場合分けすることで絶対値記号を外して考えることができます。
　

直線と二次関数に囲まれた部分の面積は1/6公式

$${\hspace{10pt}\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3 \hspace{10pt}}$$

を使用すると簡単に計算ができます。

1/6公式から計算できる面積を足し引きすることで、面積を素早く求めることができます。
　

【問題(1)の解答】
　問題 : 『曲線\(\hspace{1pt}y = |x^2-4x|\hspace{2pt}\)と直線\(\hspace{2pt}y = ax\hspace{2pt}\)が異なる\(\hspace{1pt}3\hspace{1pt}\)点を共有している。この曲線と直線に囲まれた面積を\(\hspace{1pt}S\hspace{1pt}\)とする。ただし、\(a\hspace{1pt}\)は実数とする。
　(1) \(a \hspace{2pt}\)の範囲を求めよ
　(2) 面積\(\hspace{1pt}S \hspace{2pt}\)を\(\hspace{1pt}a\hspace{1pt}\)により表せ
　(3) 面積\(\hspace{1pt}S\hspace{1pt}\)が最小値となる\(\hspace{2pt}a\hspace{2pt}\)を求めよ』
　

\(\hspace{1pt}y = |x^2-4x|\hspace{1pt}\)を因数分解すると $$ \begin{aligned} y = & |x^2 -4x|\\[0.5em] = & |x(x-4)| \\[0.5em] \end{aligned} $$ となることから
　\(x \leqq 0\hspace{2pt}\)または\(\hspace{2pt}x \geqq 4\hspace{2pt}\)のとき $${y = x(x-4) }$$ 　\(0 < x < 4\hspace{1pt}\)のとき $${y = -x(x-4) }$$ となります。

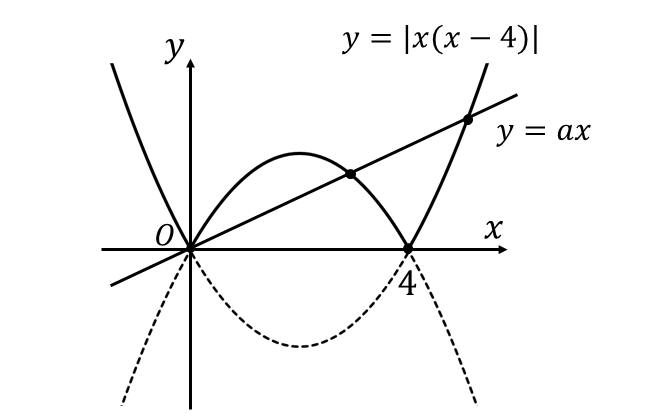
すなわち、曲線\(\hspace{1pt}y = |x(x-4)|\hspace{2pt}\)と直線\(\hspace{1pt}y = ax\hspace{1pt}\)のグラフは以下のようになります。 y=|x(x-4)|とy=axが3つの異なる共有点を持つときのグラフ

ここで、\(y = -x(x-4)\hspace{2pt}\)の\(\hspace{2pt}x=0\hspace{2pt}\)における接線の傾きは\(\hspace{1pt}f(x)=-x(x-4)\hspace{1pt}\)とすると $${f'(x) = -2x+4}$$ であることから $${f'(0) = 4}$$ となります。

上図から曲線と直線が異なる\(\hspace{1pt}3\hspace{1pt}\)つの共有点を持つとき、直線の傾き\(\hspace{1pt}a\hspace{1pt}\)が\(\hspace{2pt}a < f'(0)= 4\hspace{2pt}\)かつ\(\hspace{2pt}a > 0\hspace{2pt}\)であればよいので $${ 0 < a < 4}$$ となります。
　

【問題(2)の解答】
　問題 : 『曲線\(\hspace{1pt}y = |x^2-4x|\hspace{2pt}\)と直線\(\hspace{2pt}y = ax\hspace{2pt}\)が異なる\(\hspace{1pt}3\hspace{1pt}\)点を共有している。この曲線と直線に囲まれた面積を\(\hspace{1pt}S\hspace{1pt}\)とする。ただし、\(a\hspace{1pt}\)は実数とする。
　(1) \(a \hspace{2pt}\)の範囲を求めよ
　(2) 面積\(\hspace{1pt}S \hspace{2pt}\)を\(\hspace{1pt}a\hspace{1pt}\)により表せ
　(3) 面積\(\hspace{1pt}S\hspace{1pt}\)が最小値となる\(\hspace{2pt}a\hspace{2pt}\)を求めよ』
　

\(x \leqq 0\hspace{2pt}\)または\(\hspace{2pt}x \geqq 4\hspace{2pt}\)のとき、\(y = x(x-4)\hspace{1pt}\)と\(\hspace{1pt}y = ax\hspace{1pt}\)の共有点の\(\hspace{1pt}x\hspace{1pt}\)座標は $$ \begin{aligned} x(x-4) = & ax\\[0.5em] x^2 -(4+a)x= &0 \\[0.5em] x(x -(4+a))= &0 \\[0.5em] \end{aligned} $$ から\(\hspace{1pt}x = 0 , 4+a\hspace{1pt}\)となります。

また、\(0 < x < 4\hspace{2pt}\)のとき、\(y = -x(x-4)\hspace{1pt}\)と\(\hspace{1pt}y = ax\hspace{1pt}\)の共有点の\(\hspace{1pt}x\hspace{1pt}\)座標は $$ \begin{aligned} -x(x-4) = & ax\\[0.5em] -x^2 +(4-a)x= &0 \\[0.5em] -x(x -(4-a))= &0 \\[0.5em] \end{aligned} $$ から\(\hspace{1pt}x = 4-a\hspace{1pt}\)となります。

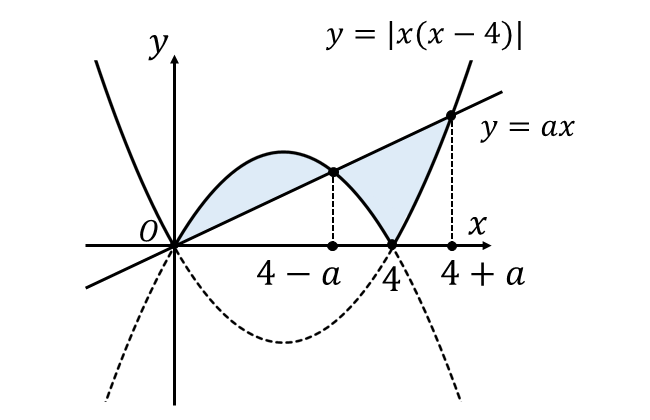
すなわち、曲線\(\hspace{1pt}y = |x(x-4)|\hspace{2pt}\)と直線\(\hspace{1pt}y = ax\hspace{1pt}\)に囲まれた部分は以下の青色の領域になります。 y=|x(x-4)|とy=axが3つの異なる共有点を持つときのグラフ

この面積を通常の定積分の計算から求めようとすると、非常に手間のかかる計算となります。

そこで、直線と二次関数に囲まれた面積を簡単に求められる1/6公式を利用し、面積を求めます。

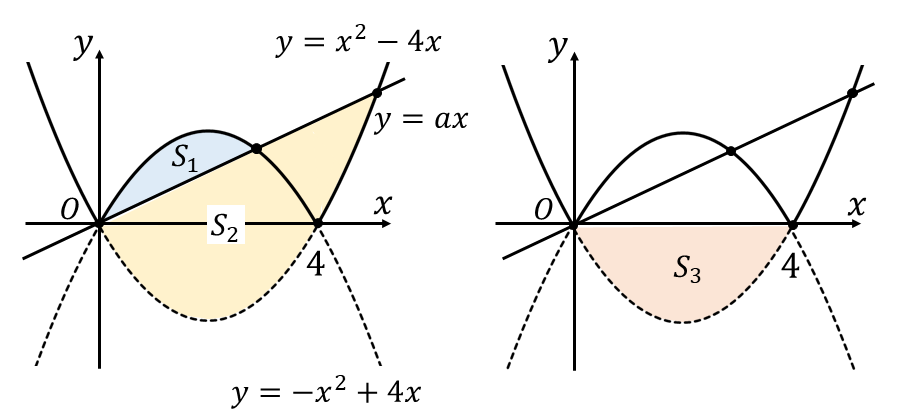
下図のように、\(y = -x^2+4x\hspace{2pt}\)と\(\hspace{2pt}y = ax\hspace{2pt}\)に囲まれた面積を\(\hspace{2pt}S_1\hspace{1pt}\)、\(y = x^2-4x\hspace{2pt}\)と\(\hspace{2pt}y = ax\hspace{2pt}\)に囲まれた面積を\(\hspace{2pt}S_2\hspace{1pt}\)、\(y = x^2-4x\hspace{2pt}\)と\(\hspace{2pt}x\hspace{1pt}\)軸に囲まれた面積を\(\hspace{2pt}S_3\hspace{2pt}\)として、それぞれの面積を求めます。 3つの面積に分けて元の面積を求める方法

以下の1/6公式

$${\hspace{10pt}\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3 \hspace{10pt}}$$

から\(\hspace{1pt}S_1 , S_2 , S_3\hspace{2pt}\)を求めると

$$ \begin{aligned} \hspace{10pt}S_1 = & \int_{0}^{4-a} (-x^2+4x - ax) dx\\[1.2em] \hspace{10pt}= & - \int_{0}^{4-a} x(x-(4 - a)) dx\\[1.2em] = & - \left\{ -\frac{1}{6}((4-a)-0)^3\right\}\\[1.2em] = & \frac{(4-a)^3}{6} \\[1em] \end{aligned} $$

$$ \begin{aligned} \hspace{10pt}S_2 = & \int_{0}^{4+a} (ax - (x^2-4x) ) dx\\[1.2em] \hspace{10pt}= & - \int_{0}^{4+a} x(x -(4+a)) dx\\[1.2em] = & - \left\{ -\frac{1}{6}((4+a)-0)^3\right\}\\[1.2em] = & \frac{(4+a)^3}{6} \\[1em] \end{aligned} $$

$$ \begin{aligned} \hspace{10pt}S_3 = & \int_{0}^{4} ( - (x^2-4x) ) dx\\[1.2em] \hspace{10pt}= & - \int_{0}^{4} x(x -4) dx\\[1.2em] = & - \left\{ -\frac{1}{6}(4-0)^3\right\}\\[1.2em] = & \frac{32}{3} \\[1em] \end{aligned} $$

求める面積\(\hspace{1pt}S\hspace{1pt}\)は

$$ \begin{aligned} \hspace{10pt}S = & S_1 +(S_1 + S_2 -2 S_3)\\[1.2em] \hspace{10pt}= & 2S_1 + S_2 - 2 S_3\\[1.2em] = & 2 \cdot \frac{(4-a)^3}{6} + \frac{(4+a)^3}{6} - 2 \cdot \frac{32}{3}\hspace{10pt}\\[1.2em] = & -\frac{1}{6}a^3 + 6a^2 -8a + \frac{32}{3} \\[1em] \end{aligned} $$

したがって、面積は\(\displaystyle\hspace{1pt}S = -\frac{1}{6}a^3 + 6a^2 -8a + \frac{32}{3} \hspace{1pt}\)となります。

【問題(2)の補足】
面積\(\hspace{1pt}S = S_1 +(S_1 + S_2 -2 S_3)\hspace{2pt}\)の\(\hspace{2pt}S_1 + S_2 -2 S_3\hspace{2pt}\)は、1/6公式から求められる面積を足し引きして、区間\(\hspace{2pt}[4-a , 4+a]\hspace{2pt}\)における面積を求めています。

図で表すと、\(S_1 + S_2\hspace{2pt}\)は以下の左図の青い領域を求めています。

また、\(2 S_3\hspace{1pt}\)は右図のオレンジ色の\(\hspace{1pt}y = x^2-4x , y = -x^2+4x\hspace{1pt}\)で囲まれた面積を求めています。

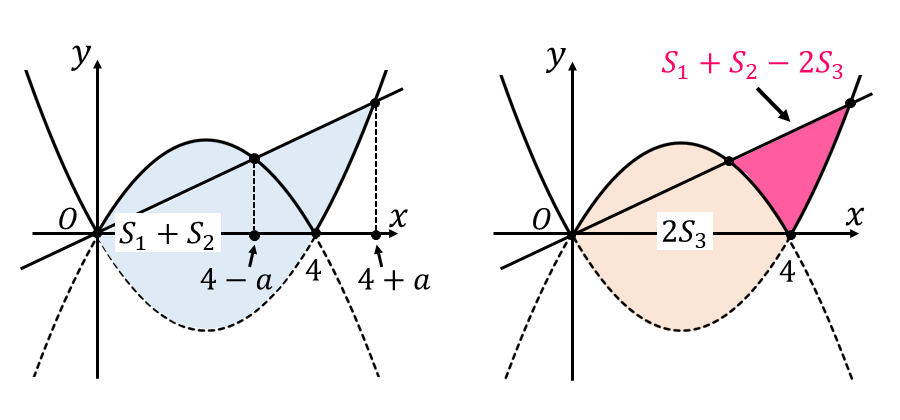
したがって、\(\hspace{1pt}S_1 + S_2 -2 S_3\hspace{1pt}\)は右図のピンク色の領域を求めています。 1/6公式から求められる面積の足し引きから求める面積
　

【問題(3)の解答】
　問題 : 『曲線\(\hspace{1pt}y = |x^2-4x|\hspace{2pt}\)と直線\(\hspace{2pt}y = ax\hspace{2pt}\)が異なる\(\hspace{1pt}3\hspace{1pt}\)点を共有している。この曲線と直線に囲まれた面積を\(\hspace{1pt}S\hspace{1pt}\)とする。ただし、\(a\hspace{1pt}\)は実数とする。
　(1) \(a \hspace{2pt}\)の範囲を求めよ
　(2) 面積\(\hspace{1pt}S \hspace{2pt}\)を\(\hspace{1pt}a\hspace{1pt}\)により表せ
　(3) 面積\(\hspace{1pt}S\hspace{1pt}\)が最小値となる\(\hspace{2pt}a\hspace{2pt}\)を求めよ』
　

問題(1)と(2)から、\(\displaystyle\hspace{2pt}0 < a < 4\hspace{2pt}\)の範囲で面積\(\displaystyle\hspace{1pt}S(a) \hspace{2pt}\)の増減表を作ることで最小値となる\(\hspace{1pt}a\hspace{1pt}\)の値を求めます。

\(\displaystyle\hspace{1pt}S(a) = -\frac{1}{6}a^3 + 6a^2 -8a + \frac{32}{3} \hspace{2pt}\)を\(\hspace{1pt}a\hspace{1pt}\)で微分すると $${S'(a) = -\frac{1}{2}a^2+12a -8}$$ \(\displaystyle\hspace{1pt}S'(a) = 0\hspace{1pt}\)となる\(\hspace{1pt}a\hspace{1pt}\)を求めると $$ -\frac{1}{2}a^2+12a -8 = 0$$ より、\(\displaystyle a = 12 - 8 \sqrt{2}\hspace{2pt}\)となります。

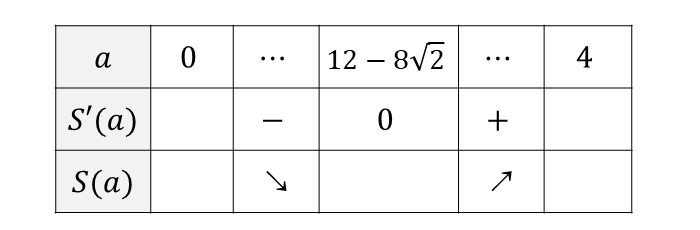
増減表は以下のようになります。 y=|x(x-4)|とy=axによって囲まれる部分の面積Sの増減表

したがって、面積\(\hspace{1pt}S\hspace{1pt}\)は\(\hspace{1pt}a = 12 - 8\sqrt{2}\hspace{1pt}\)のとき最小値となります。
　

【入試本番に向けたアドバイス】
　本問は、絶対値記号を含む二次関数と直線に囲まれた部分の面積を求める問題です。

本問のように
　(1) 特定の数の交点を持つ定数\(\hspace{1pt}a\hspace{1pt}\)の条件を求める
　(2) 面積を定数\(\hspace{1pt}a\hspace{1pt}\)を用いて表す
　(3) 面積の最小値、そのときの\(\hspace{1pt}a\hspace{1pt}\)を求める
という問題の流れは、数学Ⅱの入試問題では定番なので よく練習して慣れておくようにしましょう。

このタイプの問題のやっかいな点は、定数\(\hspace{1pt}a\hspace{1pt}\)を含む定積分は、そのまま計算すると非常に煩雑な計算になるという点です。

そのため、『いかに定積分を簡単に計算するか』が重要となります。

本問では二次関数と直線によって囲まれる面積を1/6公式

$${\hspace{10pt}\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3 \hspace{10pt}}$$

から計算し、それらの面積を足し引きすることで計算時間を短縮しています。

数学Ⅱの積分の問題は、一見すると簡単な問題でも、計算過程で時間のかかる場合が多いです。
そのため、普段から計算時間を短縮することを意識して問題を解くことが重要です。
　

【関連するページ】
・定積分

【出題範囲】　　【難易度】



　




　【問題の種類を絞る】



Copyright (c) 光学技術の基礎用語 All Rights Reserved.