三次関数とx軸に囲まれた部分の面積

【答え】
　\(\hspace{2pt}c=1\hspace{2pt}\)のときに最小値\(\displaystyle \hspace{2pt}\frac{4}{3}\hspace{1pt}\)
　

【解答のポイント】
因数定理から、三次関数\(\hspace{1pt}f(x) = x^3 + ax^2 + bx + c\hspace{1pt}\)が\(\hspace{2pt}x\hspace{1pt}\)軸に\(\hspace{2pt}x=c\hspace{2pt}\)で接しているとき、\(p\hspace{1pt}\)を実数とすると $${f(x) = (x-c)^2(x+p)}$$ と表すことができます。
　

【問題(1)の解答】
　問題 : 『関数\(\hspace{1pt}f(x) = x^3 + ax^2 + bx + c\hspace{2pt}\)が\(\hspace{2pt}x=c\hspace{2pt}\)で\(\hspace{2pt}x\hspace{1pt}\)軸に接している。ただし、\(a , b\hspace{1pt}\)が実数、\(\hspace{1pt}c > 0\hspace{2pt}\)であるとする。
　(1) \(a , b\hspace{2pt}\)を\(\hspace{2pt}c\hspace{2pt}\)により表せ
　(2) 関数\(\hspace{1pt}y = f(x)\hspace{2pt}\)と\(\hspace{2pt}x\hspace{1pt}\)軸によって囲まれた面積の最小値と、そのときの\(\hspace{2pt}c\hspace{2pt}\)を求めよ』
　

\(\hspace{1pt}p\hspace{1pt}\)を実数とすると、因数定理から関数\(\hspace{1pt}f(x) = x^3 + ax^2 + bx + c\hspace{2pt}\)は以下のように因数分解されます。

上式を展開して係数を比較すると $$ \begin{aligned} a= & p-2c \hspace{10pt}\cdots (1)\\[0.5em] b= & c^2-2cp \hspace{2pt}\cdots (2)\\[0.5em] c= & pc^2 \hspace{26pt}\cdots (3)\\[0.5em] \end{aligned} $$ となります。

\(\hspace{1pt}(3)\hspace{1pt}\)式を\(\hspace{1pt}c > 0\hspace{1pt}\)の条件で解くと $$p = \frac{1}{c}$$ となります。

よって、\(\displaystyle (1),(2)\hspace{1pt}\)式から $$ \begin{aligned} a= & \hspace{1pt}\frac{1}{c}-2c \hspace{7pt}\cdots (1)\\[0.7em] b= & \hspace{1pt} c^2-2 \hspace{10pt}\cdots (2)\\[0.5em] \end{aligned} $$ となります。
　

【問題(2)の解答】
　問題 : 『関数\(\hspace{1pt}f(x) = x^3 + ax^2 + bx + c\hspace{2pt}\)が\(\hspace{2pt}x=c\hspace{2pt}\)で\(\hspace{2pt}x\hspace{1pt}\)軸に接している。ただし、\(a , b\hspace{1pt}\)が実数、\(\hspace{1pt}c > 0\hspace{2pt}\)であるとする。
　(1) \(a , b\hspace{2pt}\)を\(\hspace{2pt}c\hspace{2pt}\)により表せ
　(2) 関数\(\hspace{1pt}y = f(x)\hspace{2pt}\)と\(\hspace{2pt}x\hspace{1pt}\)軸によって囲まれた面積の最小値と、そのときの\(\hspace{2pt}c\hspace{2pt}\)を求めよ』
　

問題(1)から、問題の関数は\(\displaystyle\hspace{2pt}f(x) = (x-c)^2 \left(x+\frac{1}{c} \right)\hspace{2pt}\)となります。

関数\(\hspace{1pt}y=f(x)\hspace{1pt}\)を図示すると、以下のようになります。

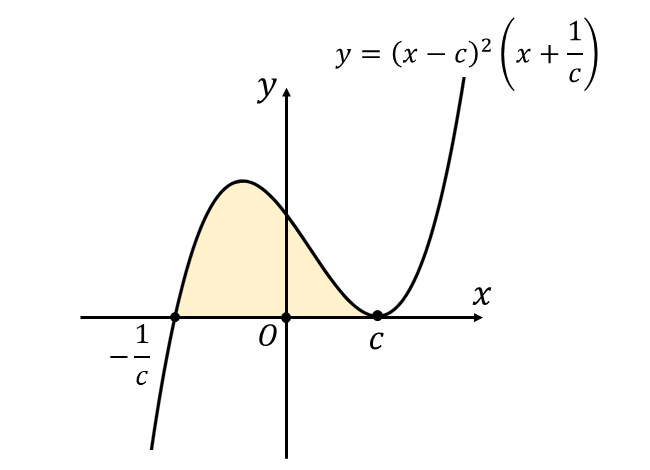
したがって、求める面積は

となります。
　

ここで、\(c > 0\hspace{1pt}\)であることから、相加・相乗平均の関係より $${c+\frac{1}{c} \geqq 2 \sqrt{c \cdot \frac{1}{c}}=2}$$ であり、等号が成立するのは\(\hspace{2pt}c=1\hspace{2pt}\)となります。

したがって、面積は\(\hspace{2pt}c=1\hspace{2pt}\)のときに最小値\(\displaystyle\hspace{2pt}\frac{4}{3}\hspace{2pt}\)となります。
　

【問題(2)の別解】
問題(2)で求める面積は、三次関数\(\hspace{1pt}f(x)=ax^3+bx^2+cx+d\hspace{1pt}\)とその曲線上の接線との接点と交点の\(\hspace{1pt}x\hspace{1pt}\)座標をそれぞれ\(\hspace{1pt}\alpha , \beta\hspace{1pt}\)としたときに囲まれた部分の面積\(\hspace{1pt}S\hspace{1pt}\)を求める1/12公式 $${S = \frac{|a|}{12}(\beta - \alpha)^4}$$ から求めることもできます。

問題の三次関数の三次の係数が\(\hspace{1pt}1\hspace{1pt}\)、\(x\hspace{1pt}\)軸との接点の\(\hspace{1pt}x\hspace{1pt}\)座標が\(\hspace{1pt}c\hspace{1pt}\)、\(x\hspace{1pt}\)軸との交点の\(\hspace{1pt}x\hspace{1pt}\)座標が\(\displaystyle\hspace{1pt}-\frac{1}{c}\hspace{1pt}\)であることから $$ \begin{aligned} \hspace{10pt} S =& \frac{|1|}{12}\left(c -\left( -\frac{1}{c}\right) \right)^4\hspace{10pt}\\[1.2em] \hspace{10pt}= & \frac{1}{12}\left( c+\frac{1}{c}\right)^4 \\[1.2em] \end{aligned}$$ となります。
　

【入試本番に向けたアドバイス】
　本問は、未知の定数で表された三次関数と\(\hspace{1pt}x\hspace{1pt}\)軸で囲まれた面積の最小値を求める問題です。

面積を求める計算では、被積分関数が $$f(x) = (x-c)^2 \left(x+\frac{1}{c} \right)$$ となり、式を展開してから積分すると文字が多くなり計算に時間がかかります。

そこで、\(n \neq -1\hspace{1pt}\)のときに成り立つ積分 $$ \begin{aligned} & \int (x-\alpha)^n\hspace{1pt}dx \\[0.5em] & = \frac{1}{n+1}(x-\alpha)^{n+1}+C\\[0.5em] \end{aligned} $$ が表れるように式を変形すると計算が簡単になります。

上記の積分は、文字を含む二次関数や三次関数の積分の問題で非常に役に立つので覚えて使えるようにしておきましょう。
　

【関連するページ】
・定積分