三角関数を積分区間に含む定積分の問題

【答え】
　\(\displaystyle\hspace{1pt}0 < \theta \leqq \frac{\pi}{3}\hspace{1pt}\)のとき
　　\(\displaystyle\hspace{1pt}\frac{1}{2} \cos^2 \theta - \frac{1}{2} \cos \theta + \frac{1}{4} \hspace{1pt}\)

　\(\displaystyle\hspace{1pt}\frac{\pi}{3} < \theta < \frac{\pi}{2}\hspace{1pt}\)のとき
　　\(\displaystyle\hspace{1pt}-\frac{1}{2} \cos^2 \theta + \frac{1}{2} \cos \theta \hspace{1pt}\)
　

【解答のポイント】
絶対値を含む定積分の問題は、絶対値を外してから積分します。

関数\(\displaystyle\hspace{1pt}f(x) =\hspace{1pt}\left | \hspace{1pt}x - \frac{1}{2} \hspace{1pt} \right | \hspace{2pt}\)は\(\displaystyle\displaystyle\hspace{2pt}x=\frac{1}{2}\hspace{2pt}\)を境界に以下のように分岐します。

また、積分区間\(\hspace{1pt}[0 , \cos \theta]\hspace{1pt}\)は\(\hspace{2pt}0 < \cos \theta < 1\hspace{2pt}\)であることから、\(\hspace{1pt}\theta\hspace{1pt}\)の値によって積分区間に\(\displaystyle\hspace{1pt}x = \frac{1}{2}\hspace{1pt}\)を含むかが変化するため、\(\theta\hspace{1pt}\)の値によって場合分けが必要になります。
　

【解答】
　問題 : 『定積分\(\displaystyle\hspace{2pt}\int_{ 0 }^{ \cos \theta} \hspace{1pt}\left | \hspace{1pt}x - \frac{1}{2} \hspace{1pt} \right | \hspace{1pt} dx\hspace{2pt}\)を求めよ。(ただし、\(\displaystyle 0 < \theta < \frac{\pi}{2}\hspace{1pt}\)とする)』

関数\(\displaystyle\hspace{1pt}f(x) =\hspace{1pt}\left | \hspace{1pt}x - \frac{1}{2} \hspace{1pt} \right | \hspace{1pt}\)は\(\displaystyle\hspace{2pt}x=\frac{1}{2}\hspace{2pt}\)を境界に絶対値記号を外したときの関数が以下のように変化します。

また、積分区間\(\hspace{1pt}[0 , \cos \theta]\hspace{1pt}\)は\(\hspace{1pt}\theta\hspace{1pt}\)の値によって\(\displaystyle\hspace{1pt}x = \frac{1}{2}\hspace{1pt}\)を含むかが以下の図のように変化します。

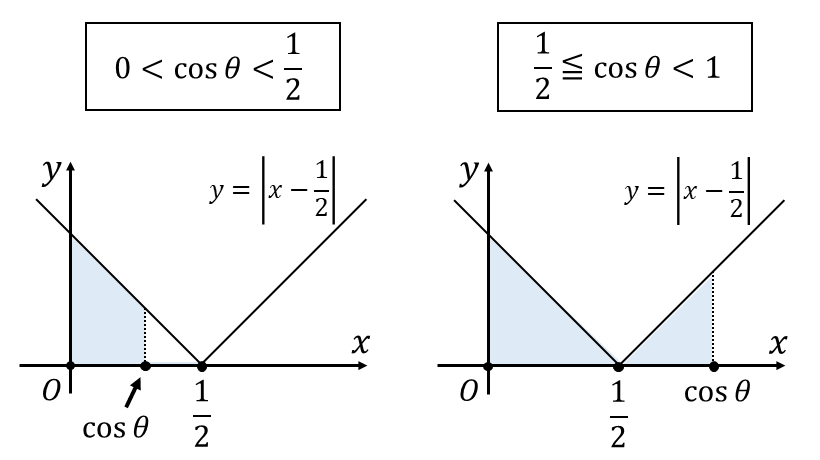
よって、以下のように場合分けをして定積分を計算します。

　[1] \(\displaystyle\hspace{1pt}0 < \cos \theta < \frac{1}{2}\hspace{1pt}\)のとき
　[2] \(\displaystyle\hspace{1pt}\frac{1}{2} \leqq \cos \theta < 1\hspace{1pt}\)のとき
　

[1] \(\displaystyle\hspace{1pt}0 < \cos \theta < \frac{1}{2}\hspace{1pt}\)のとき
　関数\(\displaystyle\hspace{1pt}f(x) =\hspace{1pt}\left | \hspace{1pt}x - \frac{1}{2} \hspace{1pt} \right | \hspace{1pt}\)と積分区間の関係は、以下の図のようになります。

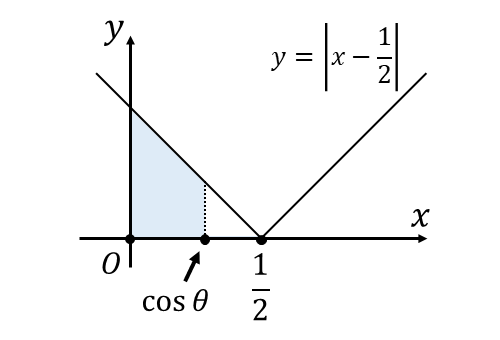
絶対値記号を外して積分すると、以下のようになります。 $$ \begin{aligned} & \int_{ 0 }^{ \cos \theta} \hspace{1pt}\left | \hspace{1pt}x - \frac{1}{2} \hspace{1pt} \right | \hspace{1pt} dx\\[1em] \hspace{10pt}=& \int_{ 0 }^{ \cos \theta} \hspace{1pt}\left ( \hspace{1pt} -x + \frac{1}{2} \hspace{1pt} \right ) \hspace{1pt} dx \\[1em] =& \left [ -\frac{1}{2}x^2 + \frac{1}{2} x \right ]_0^{\cos \theta} \\[1em] =& -\frac{1}{2} \cos^2 \theta + \frac{1}{2} \cos \theta \hspace{10pt}\\[1em] \end{aligned} $$

ここで、\(\displaystyle 0 < \cos \theta < \frac{1}{2}\hspace{1pt}\)を満たす\(\hspace{1pt}\theta\hspace{1pt}\)は $${\frac{\pi}{3} < \theta < \frac{\pi}{2}}$$ となります。

したがって、\(\displaystyle\frac{\pi}{3} < \theta < \frac{\pi}{2}\hspace{1pt}\)のとき $${-\frac{1}{2} \cos^2 \theta + \frac{1}{2} \cos \theta}$$ となります。
　

[2] \(\displaystyle\hspace{1pt}\frac{1}{2} \leqq \cos \theta < 1\hspace{1pt}\)のとき
　関数\(\displaystyle\hspace{1pt}f(x) =\hspace{1pt}\left | \hspace{1pt}x - \frac{1}{2} \hspace{1pt} \right | \hspace{1pt}\)と積分区間の関係は、以下の図のようになります。

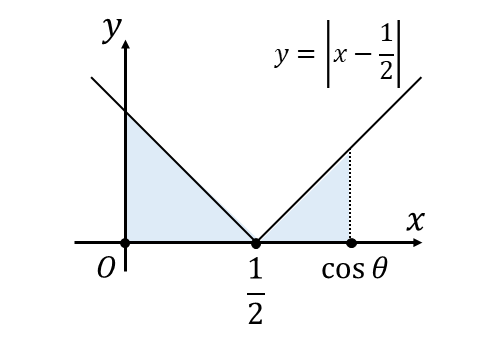
絶対値記号を外して積分すると、以下のようになります。

また、\(\displaystyle \frac{1}{2} \leqq \cos \theta < 1\hspace{1pt}\)を満たす\(\hspace{1pt}\theta\hspace{1pt}\)は $${ 0 < \theta \leqq \frac{\pi}{3}}$$ となります。

したがって、\(\displaystyle 0 < \theta \leqq \frac{\pi}{3}\hspace{1pt}\)のとき $${\frac{1}{2} \cos^2 \theta - \frac{1}{2} \cos \theta + \frac{1}{4}}$$ となります。

したがって、[1]と[2]から

　\(\displaystyle\hspace{1pt}0 < \theta \leqq \frac{\pi}{3}\hspace{1pt}\)のとき
　　\(\displaystyle\hspace{1pt}\frac{1}{2} \cos^2 \theta - \frac{1}{2} \cos \theta + \frac{1}{4} \hspace{1pt}\)

　\(\displaystyle\hspace{1pt}\frac{\pi}{3} < \theta < \frac{\pi}{2}\hspace{1pt}\)のとき
　　\(\displaystyle\hspace{1pt}-\frac{1}{2} \cos^2 \theta + \frac{1}{2} \cos \theta \hspace{1pt}\)
　

【入試本番に向けたアドバイス】
本問は、『三角関数』と『定積分』の複合問題です。

問題の定積分\(\displaystyle\hspace{2pt}\int_{0}^{\cos \theta} \left |x - \frac{1}{2} \right| dx\hspace{2pt}\)は、積分区間に三角関数が含まれていて式が複雑に見えますが定数\(\hspace{1pt}a\hspace{1pt}\)を用いると $${\int_{0}^{a} \left|x - \frac{1}{2} \right| dx}$$ となり、絶対値を含む定積分の典型的なパターンとなります。

この定積分は、以下のように積分区間\(\hspace{1pt}[0,a]\hspace{1pt}\)と\(\displaystyle\hspace{1pt}x=\frac{1}{2}\hspace{1pt}\)の位置関係によって絶対値記号の外し方が変わるため、\(a\hspace{1pt}\)の値によって場合分けをして解きます。

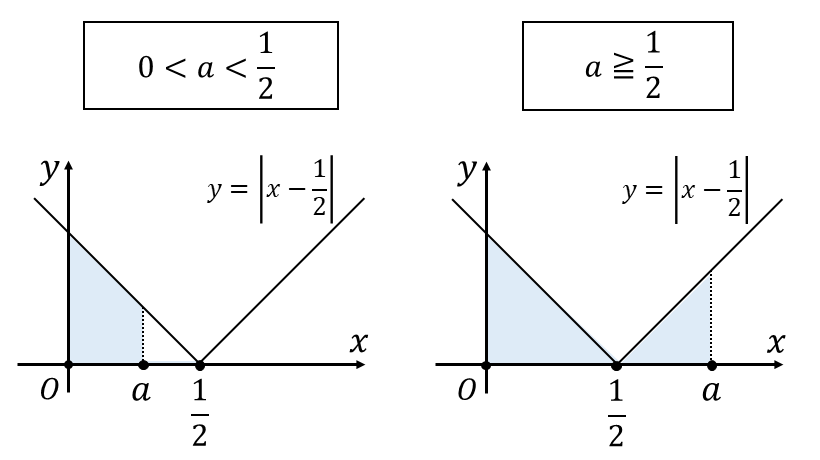
\(\displaystyle\hspace{1pt}\int_{0}^{a} | x - 1| dx\hspace{2pt}\)や\(\displaystyle\hspace{2pt}\int_{0}^{a} |1 - 2x| dx\hspace{2pt}\)など積分区間に定数を含む定積分はよく出題されるパターンの一つなので、この形式の定積分を見たら上図の場合分けをすぐに思い出せるようにしておきましょう。
　

【関連するページ】
・定積分