-光と光学に関連する用語の解説サイト-

二重の絶対値記号を含む定積分の問題

◆第問目！

【 数Ⅱ : 難易度 ★★★ 】
　　次の定積分を求めよ(ただし、\(a > 0\hspace{1pt}\)とする) $$ {\int_{0}^{2} \left | |x-1| - a \right |dx }$$

被積分関数に絶対値記号を含む場合、絶対値を外して積分する必要があります。

絶対値記号は、中身が正か負かで場合分けをすることで外すことができます。 $$|x| = \begin{dcases} x & ( x \geqq 0 ) \\ -x & ( x \lt 0 ) \end{dcases} $$

本問のように二重で絶対値記号が付いている場合は、まず内側の絶対値記号が外れるように場合分けします。

また、本問は被積分関数に定数\({\hspace{1pt}a\hspace{2pt}}\)が含まれているため、\({a\hspace{2pt}}\)の値による場合分けも必要となります。

【答え】
　\(\hspace{1pt}0 < a < 1\hspace{1pt}\)のとき
　　\(\hspace{1pt}2a^2 -2a +1 \hspace{1pt}\)

　\(\hspace{1pt}a \geqq 1\hspace{1pt}\)のとき
　　\(\hspace{1pt}2a-1 \hspace{1pt}\)
　

【解答のポイント】
絶対値を含む定積分の問題は、まず場合分けをして絶対値を外します。

このとき、本問のように二重で絶対値記号が付いている場合は、まず内側の絶対値記号から外すと考えやすいです。

本問では、被積分関数が\(\hspace{2pt}f(x) = \left | |x-1| - a \right |\hspace{2pt}\)であるので、内側の\(\hspace{1pt}|x-1|\hspace{1pt}\)の絶対値が外れるように
　・\(\hspace{2pt}x \geqq 1\hspace{1pt}\)のとき
　・\(\hspace{2pt}x < 1\hspace{1pt}\)のとき
で場合分けします。
　

また、本問は被積分関数に定数\({\hspace{1pt}a\hspace{2pt}}\)が含まれているため、\({a\hspace{2pt}}\)の値による場合分けも必要となります。

そこで、被積分関数\(\hspace{2pt}f(x) = \left | |x-1| - a \right |\hspace{2pt}\)のグラフを描くことで、\(a\hspace{1pt}\)の値によってどのような場合分けが必要かを考えます。
　

【解答】
　問題 : 『定積分\(\displaystyle\hspace{2pt}\int_{0}^{2} \left | |x-1| - a \right |dx\hspace{2pt}\)を求めよ。(ただし、\(a > 0\hspace{1pt}\)とする)』

まず、\(x\hspace{1pt}\)の範囲で場合分けして\(\hspace{2pt}y = \left | |x-1| - a \right |\hspace{2pt}\)のグラフを描きます。

\(\hspace{1pt}x \geqq 1\hspace{1pt}\)のとき
　\(\hspace{1pt}|x-1| = x-1\hspace{1pt}\)であることから $$ {\left | |x-1| - a \right | = |x-1 - a| }$$ 　となります。

\(\hspace{1pt}x < 1\hspace{1pt}\)のとき
　\(\hspace{1pt}|x-1| = -(x -1)\hspace{1pt}\)であることから $$ {\left | |x-1| - a \right | = |-x + 1 - a| }$$ 　となります。

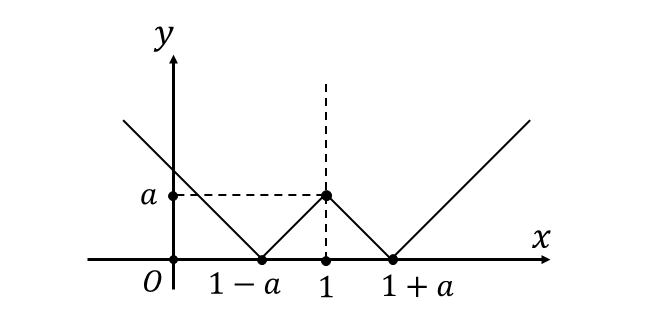
　以上から、\(y = \left | |x-1| - a \right |\hspace{1pt}\)のグラフを描くと以下のようになります。 2つの絶対値記号を含む定積分の問題

ここで、積分区間が\({\hspace{1pt}[0,2]\hspace{2pt}}\)であることから、積分区間に\({\hspace{1pt}x=1-a\hspace{2pt}}\)が含まれる \({0 < a < 1\hspace{2pt}}\)のときと、積分区間の外側に\({\hspace{1pt}x=1-a\hspace{2pt}}\)が位置する \({ a \geqq 1\hspace{2pt}}\)のときで場合分けします。
　

[1] \(\hspace{1pt}0 < a < 1\hspace{1pt}\)のとき
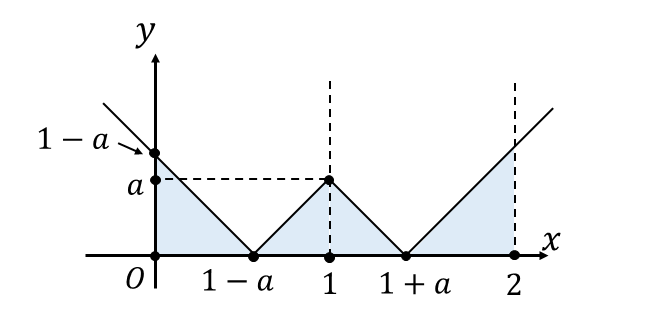
　このとき、グラフは以下のようになります。 2つの絶対値記号を含む定積分の問題

すなわち、求める定積分は以下のようになります。

$$ \begin{aligned} & \int_{0}^{2} \left | |x-1| - a \right |dx\\[1em] \hspace{10pt}=& 2 \int_{0}^{1}|-x + 1 - a|dx \\[1em] =& 2 \left \{\int_{0}^{1-a}(-x + 1 - a)dx + \int_{1-a}^{1} -(-x + 1 - a) dx \right \}\hspace{10pt}\\[1em] =& 2 \left \{ \left [ -\frac{1}{2}x^2 +(1-a)x \right ]_0^{1-a} + \left [ \frac{1}{2}x^2 +(-1+a)x \right ]_{1-a}^1 \right \}\hspace{10pt}\\[1em] =& -(1-a)^2 + 2(1-a)^2 + (1-(1-a)^2) +2(-1+a)a \hspace{10pt}\\[1em] =& 2a^2 -2a +1 \\ \end{aligned} $$

[2] \(\hspace{1pt} a \geqq 1\hspace{1pt}\)のとき
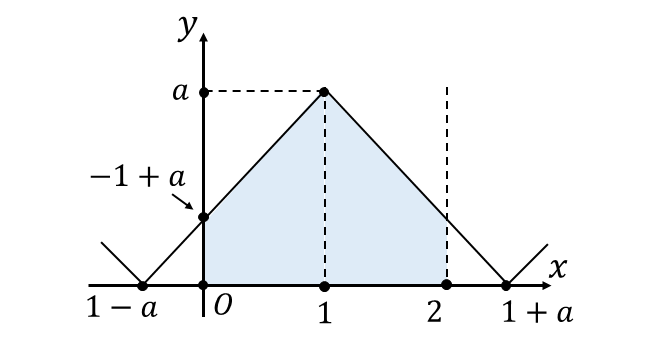
　このとき、グラフは以下のようになります。 2つの絶対値記号を含む定積分の問題

すなわち、求める定積分は以下のようになります。

$$ \begin{aligned} & \int_{0}^{2} \left | |x-1| - a \right |dx\\[1em] \hspace{10pt}=& 2 \int_{0}^{1}|-x + 1 - a|dx \\[1em] =& 2 \int_{0}^{1} -(-x + 1 - a) dx \hspace{10pt}\\[1em] =& 2 \left [ \frac{1}{2}x^2 +(-1+a)x \right ]_0^{1} \hspace{10pt}\\[1em] =& 1 + 2(-1+a) \hspace{10pt}\\[1em] =& 2a-1 \\ \end{aligned} $$

したがって、[1]と[2]から
　\(\hspace{1pt}0 < a < 1\hspace{1pt}\)のとき
　　\(\hspace{1pt}2a^2 -2a +1 \hspace{1pt}\)

　\(\hspace{1pt}a \geqq 1\hspace{1pt}\)のとき
　　\(\hspace{1pt}2a-1 \hspace{1pt}\)
　

【別解】
本問は、\(x\hspace{1pt}\)の一次関数であるため、グラフから面積を求めることができます。

[1] \(\hspace{1pt}0 < a < 1\hspace{1pt}\)のとき
下図の\(\hspace{1pt}y=\left | |x-1| - a \right |\hspace{1pt}\)、\(x\hspace{1pt}\)軸、\(x=0\hspace{1pt}\)、\(x=2\hspace{1pt}\)に囲まれた面積\(\hspace{1pt}S_1\hspace{1pt}\)を求めます。 2つの絶対値記号を含む定積分の問題

$$ \begin{aligned} S_1 & = 2 \left\{ \frac{1}{2}(1-a)^2 + \frac{1}{2}a^2 \right \}\\[1em] \hspace{10pt}=& (1-a)^2 + a^2 \\[1em] =& 2a^2 - 2a + 1 \\[1em] \end{aligned} $$

すなわち、\(0 < a < 1\hspace{1pt}\)のとき $$ \begin{aligned} & \int_{0}^{2} \left | |x-1| - a \right |dx\\[1em] & = 2a^2 - 2a + 1 \\ \end{aligned} $$ となります。
　

[2] \(\hspace{1pt} a \geqq 1\hspace{1pt}\)のとき
下図の\(\hspace{1pt}y=\left | |x-1| - a \right |\hspace{1pt}\)、\(x\hspace{1pt}\)軸、\(x=0\hspace{1pt}\)、\(x=2\hspace{1pt}\)に囲まれた面積\(\hspace{1pt}S_2\hspace{1pt}\)を求めます。 2つの絶対値記号を含む定積分の問題

$$ \begin{aligned} S_2 & = 2 \left\{ \frac{1}{2} a^2 - \frac{1}{2} (a-1)^2\right \}\\[1em] \hspace{10pt}=& a^2 - (a-1)^2 \\[1em] =& 2a -1 \\[1em] \end{aligned} $$

すなわち、\( a \geqq 1\hspace{1pt}\)のとき $$ \begin{aligned} & \int_{0}^{2} \left | |x-1| - a \right |dx\\[1em] & = 2a -1 \\ \end{aligned} $$ となります。
　

したがって、[1]と[2]から
　\(\hspace{1pt}0 < a < 1\hspace{1pt}\)のとき
　　\(\hspace{1pt}2a^2 -2a +1 \hspace{1pt}\)

　\(\hspace{1pt}a \geqq 1\hspace{1pt}\)のとき
　　\(\hspace{1pt}2a-1 \hspace{1pt}\)
　

【入試本番に向けたアドバイス】
定積分の問題は、可能な限り定積分を計算しないことが計算時間の短縮に重要となります。

別解に示したように、本問は\(\hspace{1pt}x\hspace{1pt}\)の一次関数であるため、定積分の値を三角形の面積から求めることができます。

特に、本問のように絶対値記号を含む\(x\hspace{1pt}\)の一次関数は、積分区間がいくつかに分けられて定積分の計算が煩雑になるため、面積から求めると計算が楽になります。
　

他に定積分の計算を省く方法として二次関数の定積分で使用される1/6公式

$${\hspace{10pt}\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3 \hspace{10pt}}$$

があります。数学Ⅱの分野では頻出であるため、必ず覚えて使えるようにしておきましょう。
　

また、数学Ⅲの範囲では、定積分の計算を省く手法として\(\displaystyle\hspace{1pt}\int_{-a}^a \sqrt{a^2-x^2} \hspace{1pt} dx\hspace{1pt}\)が半径\({a\hspace{2pt}}\)の円の面積の半分となることから $${\int_{-a}^a \sqrt{a^2-x^2} \hspace{1pt} dx = \frac{\pi}{2}a^2}$$ となります。こちらも数学Ⅲでは頻出のため覚えておきましょう。(円の面積を求める積分)
　

【関連するページ】
・定積分

【出題範囲】　　【難易度】



　




　【問題の種類を絞る】



Copyright (c) 光学技術の基礎用語 All Rights Reserved.