絶対値を含む定積分
◆第問目！
被積分関数に絶対値記号を含む場合、絶対値を外して積分する必要があります。
絶対値記号は、中身が正か負かで場合分けをすることで外すことができます。 $$|x| = \begin{dcases} x & ( x \geqq 0 ) \\ -x & ( x \lt 0 ) \end{dcases} $$
本問は被積分関数に定数\({\hspace{1pt}a\hspace{2pt}}\)が含まれているため、\({a\hspace{2pt}}\)の値によって場合分けして解きます。
被積分関数の\({\hspace{1pt}y=x^2-a^2\hspace{2pt}}\)を因数分解し、グラフを描くことで符号の変化を調べます。
【解答のポイント】
絶対値記号を含む場合、絶対値記号を外して積分する必要があります。
絶対値記号は、中身が正か負かで場合分けをすることで外すことができます。 $$|x| = \begin{dcases} x & ( x \geqq 0 ) \\ -x & ( x \lt 0 ) \end{dcases} $$
問題を解くときは、まず\({\hspace{1pt}y=x^2-a^2\hspace{2pt}}\)を因数分解し、グラフを描くことで符号が変化するイメージがしやすくなります。
【解答】
まず、被積分関数\({\hspace{1pt}y=x^2-a^2\hspace{2pt}}\)を因数分解すると
$${y=(x+a)(x-a)}$$
となります。
つまり、関数\({\hspace{1pt}y=x^2-a^2\hspace{2pt}}\)は\({\hspace{1pt}x\hspace{2pt}}\)軸と\({\hspace{1pt}x=\pm a\hspace{2pt}}\)で交点を持ちます。
ここで、積分区間が\({\hspace{1pt}[0,2]\hspace{2pt}}\)であることから、積分区間に\({\hspace{1pt}x=a\hspace{2pt}}\)が含まれる \({0 < a < 2\hspace{2pt}}\)のときと、積分区間の外側に\({\hspace{1pt}x=a\hspace{2pt}}\)が位置する \({ a \geqq 2\hspace{2pt}}\)のときで場合分けすることができます。
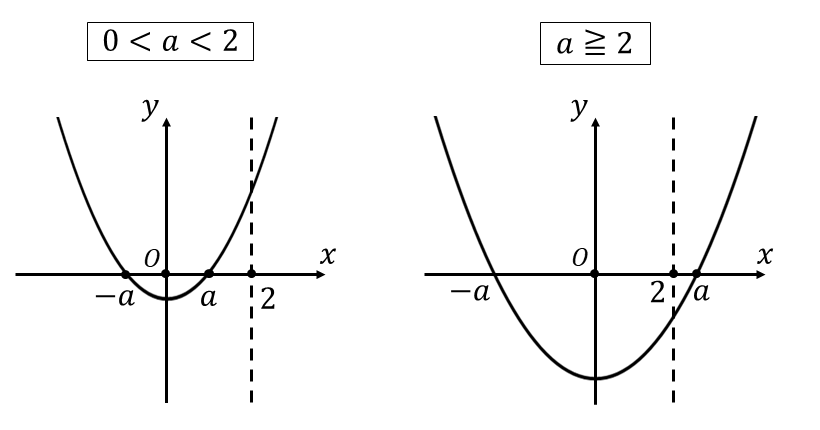
上記のグラフから、積分区間\({\hspace{1pt}[0,2]\hspace{2pt}}\)における\({\hspace{1pt}y=x^2-a^2\hspace{2pt}}\)の符号を調べ、絶対値記号を外します。
【\({0 < a < 2\hspace{2pt}}\)の場合】
\({0 \leqq x \leqq a\hspace{1pt}}\)のとき
$${|x^2-a^2|=-(x^2-a^2)}$$
\({a \leqq x \leqq 2\hspace{1pt}}\)のとき
$${|x^2-a^2|=x^2-a^2}$$
であることから
【\({a \geqq 2\hspace{2pt}}\)の場合】
\({0 \leqq x \leqq 2\hspace{1pt}}\)のとき $${|x^2-a^2|=-(x^2-a^2)}$$ であることから
以上から
\({0 < a < 2\hspace{2pt}}\)のとき
$${ \int_{0}^{2} |x^2 - a^2|dx= \frac{4}{3}a^3 -2a^2 + \frac{8}{3}}$$
\({a \geqq 2\hspace{2pt}}\)のとき
$${ \int_{0}^{2} |x^2 - a^2|dx= 2a^2-\frac{8}{3}}$$
【関連するページ】
・定積分