-光と光学に関連する用語の解説サイト-
x軸と放物線に囲まれた面積
◆第問目!
【 数Ⅱ : 難易度 ★ 】
放物線\({\hspace{2pt}y=x^2-2x-8\hspace{2pt}}\)と\({\hspace{2pt}x}\)軸に囲まれた面積\({S\hspace{2pt}}\)を求めよ
面積を求める問題は、グラフを描いて関数の上下関係を調べてから積分します。
以下の1/6公式
$${\hspace{10pt}\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3 \hspace{10pt}}$$
を利用すると計算が簡単になります。
【答え】
\(\hspace{1pt}36\hspace{1pt}\)
【解答のポイント】
面積を求める問題は、まずグラフを描いて関数の上下関係を調べてから積分します。
以下の1/6公式
$${ \hspace{10pt} \int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3 \hspace{10pt}}$$
が利用できるように因数分解すると簡単に計算することができます。(別解に記載)
【解答】
問題 : 『放物線\({\hspace{2pt}y=x^2-2x-8\hspace{2pt}}\)と\({\hspace{2pt}x}\)軸に囲まれた面積\({S\hspace{2pt}}\)を求めよ』
\({y=x^2-2x-8\hspace{3pt}}\)を因数分解すると
$$x^2-2x-8= (x+2)(x-4) \\[1em]$$
となります。したがって、放物線のグラフを描くと以下のようになります。
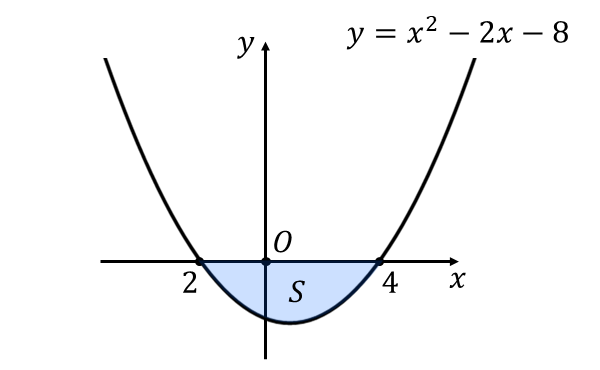
上図から、\({-2 \leqq x \leqq 4\hspace{2pt}}\)において放物線は\({\hspace{1pt}x}\)軸の下側に位置するため、面積\({\hspace{1pt}S\hspace{2pt}}\)は以下のように求められます。
$$
\begin{aligned}
\hspace{10pt}& \int_{-2}^{4} -(x^2-2x-8)\hspace{1pt} dx\\[1em]
& \int_{-2}^{4} (-x^2+2x+8)\hspace{1pt} dx\\[1em]
&=\left[ -\frac{1}{3}x^3 + x^2+ 8x \right]_{-2}^{4} \\[1em]
&= -\frac{1}{3}(4^3-(-2)^3) + 4^2-(-2)^2 + 8(4-(-2))\hspace{10pt} \\[1em]
&= -24 +12 + 48 \\[1em]
&= 36\\[1em]
\end{aligned}
$$
【別解】
以下の1/6公式
$${\hspace{10pt} \int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3 \hspace{10pt}}$$
から定積分を計算すると
$$
\begin{aligned}
& \int_{-2}^{4} -(x^2-2x-8)\hspace{1pt} dx\\[1em]
=& -\int_{-2}^{4} (x+2)(x-4)\hspace{1pt} dx\\[1em]
&=\frac{(4-(-2))^3}{6} \\[1em]
&= 36\\[1em]
\end{aligned}
$$
【関連するページ】
・定積分
【出題範囲】 【難易度】
【問題の種類を絞る】
【問題の種類を絞る】