ベータ関数と面積・回転体の体積の問題

【問題(1)の答え】
　$\displaystyle \frac{1}{m+1} $
　

【問題(2)の答え】
　証明問題のため省略
　

【問題(3)の答え】
　$\displaystyle \frac{ m! n!}{(m+n+1)! } $
　

【問題(4)の答え】
　$\displaystyle \frac{ a! b!}{(a+b)! } $
　

【問題(5)の答え】
　$\displaystyle \frac{ (2a)! b!}{(2a+b)! }\pi $
　

【解答のポイント】
本問の定積分 $${ \int_0^1 x^m (1-x)^n \hspace{1pt} dx}$$ はベータ関数と呼ばれ、統計学や物理など様々な分野で登場する定積分です。

ベータ関数は大学で学習する内容ですが、本問では高校数学で扱える範囲で$\hspace{1pt}(m,n)\hspace{1pt}$を定義しています。
　

問題(2)の証明問題は

$$\hspace{10pt}B(m,n) = \frac{n}{m+1} B(m+1 , n-1)\hspace{10pt}$$

を示す問題ですが、左辺と右辺を比較すると$\hspace{1pt}B(m,n)\hspace{1pt}$が$\hspace{1pt}B(m+1 , n-1)\hspace{1pt}$となっています。

つまり、$\hspace{1pt}x^m\hspace{1pt}$の次数が大きくなり、$\hspace{1pt}(1-x)^n\hspace{1pt}$の次数が小さくなっていることから、部分積分を利用して式を導きます。

問題(3)では、問題(2)で示した等式より$\hspace{1pt}B(m,n)\hspace{1pt}$を$\hspace{1pt}n\hspace{1pt}$に対する漸化式のように考えて、簡単な定積分になるように変形します。
　

問題(4)は、まず曲線$\displaystyle \hspace{2pt}x^{1/a}+y^{1/b} = 1\hspace{2pt}$のグラフの概形を描きます。
定義域や$\hspace{1pt}f'(x)\hspace{1pt}$の符号、$x\hspace{1pt}$軸と$\hspace{1pt}y\hspace{1pt}$軸との交点など、グラフの概形が分かるように調べます。

グラフの面積は曲線の式を$\hspace{2pt}y\hspace{2pt}$について解き $${S = \int_0^1 y \hspace{1pt}dx}$$ から求めることができます。

置換積分から問題(3)の$\hspace{1pt}B(m,n)\hspace{1pt}$が使えるように変形します。
　

【問題(1)の解答】
　問題 :『$\hspace{2pt}0\hspace{1pt}$以上の整数$\hspace{2pt}m,n\hspace{2pt}$に対して$\displaystyle\hspace{1pt}B(m,n) = \int_0^1 x^m (1-x)^n \hspace{1pt} dx\hspace{1pt}$とする. $B(m,0)\hspace{2pt}$を求めよ.』
　

$\hspace{1pt}B(m,0)\hspace{1pt}$を求めると $$ \begin{aligned} &B(m,0)\\[0.5em] & = \int_0^1 x^m (1-x)^0 \hspace{1pt} dx \\[0.5em] & = \int_0^1 x^m \hspace{1pt} dx \\[0.5em] &= \left[\frac{x^{m+1}}{m+1} \right]_0^1 \\[0.5em] &= \frac{1}{m+1} \\ \end{aligned} $$

となります。
　

【問題(2)の解答】
　問題 :『$\hspace{2pt}0\hspace{1pt}$以上の整数$\hspace{2pt}m,n\hspace{2pt}$に対して$\displaystyle\hspace{1pt}B(m,n) = \int_0^1 x^m (1-x)^n \hspace{1pt} dx\hspace{1pt}$とする.
　$n \geqq 1\hspace{1pt}$であるとき, $\displaystyle B(m,n) = \frac{n}{m+1} B(m+1 , n-1)\hspace{1pt}$が成り立つことを示せ.』
　

部分積分から

$$ \begin{aligned} \hspace{10pt} &B(m,n) \\[0.5em] \hspace{10pt} & = \int_0^1 x^m (1-x)^n \hspace{1pt} dx \\[1em] &= \left[\frac{x^{m+1}}{m+1} (1-x)^n \right]_0^1 + n \int_0^1 \frac{x^{m+1}}{m+1} (1-x)^{n-1} \hspace{1pt} dx \hspace{10pt}\\[1em] &= \frac{n}{m+1} \int_0^1 x^{m+1} (1-x)^{n-1} \hspace{1pt} dx \hspace{10pt}\\[1em] &= \frac{n}{m+1} B(m+1 , n-1) \hspace{10pt}\\[1em] \end{aligned} $$

となります。すなわち

$${\hspace{10pt}B(m,n) = \frac{n}{m+1} B(m+1 , n-1)}\hspace{10pt}$$

が成り立ちます。

【問題(3)の解答】
　問題 :『$\hspace{2pt}0\hspace{1pt}$以上の整数$\hspace{2pt}m,n\hspace{2pt}$に対して$\displaystyle\hspace{1pt}B(m,n) = \int_0^1 x^m (1-x)^n \hspace{1pt} dx\hspace{1pt}$とする. $\displaystyle B(m,n)\hspace{1pt}$を求めよ.』
　

問題(1),(2)の結果から

$$ \begin{aligned} \hspace{10pt} &B(m,n)\\[0.5em] &= \frac{n}{m+1} B(m+1 , n-1) \hspace{10pt}\\[1em] &= \frac{n}{m+1} \cdot \frac{n-1}{m+2} B(m+2 , n-2) \hspace{10pt}\\[1em] &= \cdots \hspace{10pt}\\[1em] &= \frac{n}{m+1} \cdot \frac{n-1}{m+2} \cdot \cdots \cdot \frac{1}{m+n} B(m+n , 0) \hspace{10pt}\\[1em] &= \frac{n!}{(m+n)! / m!} B(m+n , 0) \hspace{10pt}\\[1em] &= \frac{ m! n!}{(m+n)! } B(m+n , 0) \hspace{10pt}\\[1em] &= \frac{ m! n!}{(m+n)! } \int_0^1 x^{m+n} (1-x)^0 \hspace{1pt} dx\hspace{10pt}\\[1em] &= \frac{ m! n!}{(m+n)! } \left[\frac{x^{m+n+1} }{m+n+1} \right]_0^1 \hspace{10pt}\\[1em] &= \frac{ m! n!}{(m+n+1)! } \hspace{10pt}\\[1em] \end{aligned} $$

となります。
　

【問題(4)の解答】
　問題 :『$\hspace{2pt}0\hspace{1pt}$以上の整数$\hspace{2pt}m,n\hspace{2pt}$に対して$\displaystyle\hspace{1pt}B(m,n) = \int_0^1 x^m (1-x)^n \hspace{1pt} dx\hspace{1pt}$とする.
　$a,b\hspace{1pt}$が自然数である曲線$\displaystyle \hspace{2pt}x^{1/a}+y^{1/b} = 1\hspace{2pt}$$\hspace{1pt}(x \geqq 0 , y \geqq 0)\hspace{1pt}$と$\hspace{2pt}x\hspace{1pt}$軸, $y\hspace{1pt}$軸に囲まれた領域$\hspace{1pt}A\hspace{1pt}$の面積$\hspace{1pt}S\hspace{1pt}$を求めよ.』
　

まず、$\displaystyle x^{1/a}+y^{1/b} = 1\hspace{2pt}$の定義域を調べます。

曲線の式を変形すると $${y^{1/b} = 1-x^{1/a}}$$ $y^{1/b} \geqq 0\hspace{1pt}$より$\hspace{1pt}1-x^{1/a} \geqq 0\hspace{1pt}$であることから $${1 \geqq x^{1/a}}$$ すなわち $${1 \geqq x}$$ $\hspace{1pt}x \geqq 0\hspace{1pt}$と共通部分をとると $${0 \leqq x \leqq 1}$$ となります。$\hspace{1pt}y\hspace{1pt}$についても同様に $${0 \leqq y \leqq 1}$$ となります。

$\hspace{1pt}f(x) = (1-x^{1/a})^b\hspace{1pt}$とおいて関数$\hspace{1pt}f(x)\hspace{2pt}$の導関数を求めると

$$ \begin{aligned} \hspace{10pt} f'(x) & = b (1-x^{1/a})^{b-1} \cdot \left(-\frac{1}{a}x^{\frac{1}{a}-1} \right) \hspace{10pt}\\[0.7em] \hspace{10pt} & = -\frac{b}{a} (1-x^{1/a})^{b-1} \left(x^{\frac{1-a}{a}} \right) \hspace{10pt}\\[0.7em] \end{aligned} $$

よって、$0 < x < 1\hspace{1pt}$において$\hspace{2pt}f'(x) < 0\hspace{2pt}$であることから、$y = f(x)\hspace{1pt}$は単調に減少します。

また、$f(0) = 1\hspace{1pt} , f(1) = 0\hspace{2pt}$となります。

以上から、$y = f(x)\hspace{1pt}$のグラフの概形は以下のようになります。
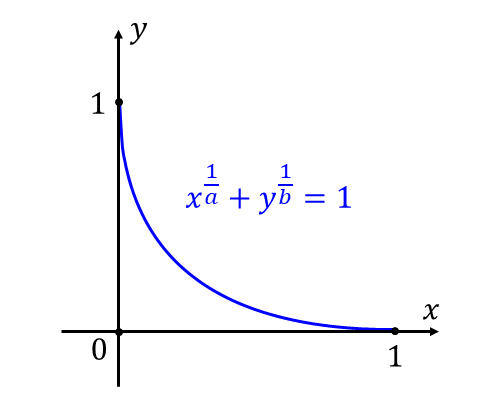
($\hspace{2pt}(a,b)=(2,2)\hspace{2pt}$のときのグラフを描いています。) 曲線x^(1/a)+y^(1/b)=1に囲まれた面積を求める問題

上記のグラフから、求める面積$\hspace{1pt}S\hspace{1pt}$は $${S =\int_0^1 (1-x^{1/a})^b \hspace{1pt} dx}$$ となります。ここで、$\displaystyle t = x^{1/a}\hspace{1pt}$とおくと、$x = t^a\hspace{2pt}$となります。

また、変数${\hspace{1pt}x\hspace{1pt}}$の範囲に対応する変数${\hspace{1pt}t\hspace{1pt}}$を求めると、以下のようになります。

${x}$	${\displaystyle 0 \to 1}$
${t}$	$\displaystyle{0 \to 1}$

${\displaystyle x = t^a}$ の両辺を ${t}$ で微分すると$\displaystyle\hspace{1pt}\frac{dx}{dt} = a t^{a-1}\hspace{1pt}$となります。すなわち、$\displaystyle{dx = a t^{a-1}\hspace{1pt} dt}$ と表せます。

したがって、求める面積$\hspace{1pt}S\hspace{1pt}$は

$$ \begin{aligned} \hspace{10pt}S = & \int_0^1 (1-x^{1/a})^b \hspace{1pt} dx \hspace{10pt}\\[0.7em] \hspace{10pt}&= \int_0^1 (1-t)^b \cdot a t^{a-1}\hspace{1pt} dt \hspace{10pt}\\[0.7em] \hspace{10pt}&= a \int_0^1 t^{a-1}(1-t)^b \hspace{1pt} dt \hspace{10pt}\\[0.7em] \hspace{10pt}&= a B(a-1 , b) \hspace{10pt}\\[0.7em] \hspace{10pt}&= a \frac{ (a-1)! b!}{(a-1+b+1)! } \hspace{10pt}\\[0.7em] \hspace{10pt}&= \frac{ a! b!}{(a+b)! } \hspace{10pt}\\ \end{aligned} $$

と求められます。
　

【問題(5)の解答】
　問題 :『$\hspace{2pt}0\hspace{1pt}$以上の整数$\hspace{2pt}m,n\hspace{2pt}$に対して$\displaystyle\hspace{1pt}B(m,n) = \int_0^1 x^m (1-x)^n \hspace{1pt} dx\hspace{1pt}$とする.
　$a,b\hspace{1pt}$が自然数である曲線$\displaystyle \hspace{2pt}x^{1/a}+y^{1/b} = 1\hspace{2pt}$$\hspace{1pt}(x \geqq 0 , y \geqq 0)\hspace{1pt}$と$\hspace{2pt}x\hspace{1pt}$軸, $y\hspace{1pt}$軸に囲まれた領域$\hspace{1pt}A\hspace{1pt}$を$\hspace{1pt}y\hspace{1pt}$軸の周りに回転させた回転体の体積$\hspace{1pt}V\hspace{1pt}$を求めよ.』
　

問題(4)のグラフから、求める回転体の体積$\hspace{1pt}V\hspace{1pt}$は $${V = \pi \int_0^1 x^2 \hspace{1pt} dy}$$ となります。

$\displaystyle x^{1/a}+y^{1/b} = 1\hspace{2pt}$を変形すると $$ \begin{aligned} x^{1/a} & = 1- y^{1/b}\\[0.5em] x &= (1- y^{1/b})^a\\ \end{aligned} $$ となります。よって、求める体積は $${V = \pi \int_0^1 (1- y^{1/b})^{2a} \hspace{1pt} dy}$$ となります。

ここで、$\displaystyle t = y^{1/b}\hspace{1pt}$とおくと、$y = t^b\hspace{2pt}$となります。

また、変数${\hspace{1pt}y\hspace{1pt}}$の範囲に対応する変数${\hspace{1pt}t\hspace{1pt}}$を求めると、以下のようになります。

${y}$	${\displaystyle 0 \to 1}$
${t}$	$\displaystyle{0 \to 1}$

${\displaystyle y = t^b}$ の両辺を ${t}$ で微分すると$\displaystyle\hspace{1pt}\frac{dy}{dt} = b t^{b-1}\hspace{1pt}$となります。すなわち、$\displaystyle{dy = b t^{b-1}\hspace{1pt} dt}$ と表せます。

したがって、求める体積は

$$ \begin{aligned} \hspace{10pt}V &=\pi \int_0^1 (1- y^{1/b})^{2a} \hspace{1pt} dy \hspace{10pt}\\[0.7em] \hspace{10pt}&=\pi \int_0^1 (1- t)^{2a} \cdot b t^{b-1}\hspace{1pt} dt \hspace{10pt}\\[0.7em] \hspace{10pt}&= b \pi \int_0^1 t^{b-1} (1- t)^{2a} \hspace{1pt} dt \hspace{10pt}\\[0.7em] \hspace{10pt}&= b \pi B(b-1 , 2a) \hspace{10pt}\\[0.7em] \hspace{10pt}&= b \pi \frac{ (b-1)! (2a)!}{(b-1+2a+1)! } \hspace{10pt}\\[0.7em] \hspace{10pt}&= \frac{ (2a)! b!}{(2a+b)! }\pi \hspace{10pt}\\ \end{aligned} $$

と求められます。
　

【入試本番に向けたアドバイス】
本問は定積分 $${B(m,n) =\int_0^1 x^m (1-x)^n \hspace{1pt} dx}$$ を求めた後、曲線の面積と体積を求める問題です。

ベータ関数は入試問題ではよく出題されるテーマの一つです。

『$B(m,n)\hspace{1pt}$の値を求める過程』や『曲線$\hspace{2pt}x^\frac{1}{a} + y^\frac{1}{b} = 1\hspace{2pt}$と$\hspace{1pt}x\hspace{1pt}$軸と$\hspace{1pt}y\hspace{1pt}$軸に囲まれた面積は$\hspace{2pt}B(m,n)\hspace{2pt}$により表される』ことは知識として覚えておきましょう。
　

また、以下の定積分 $${\int_\alpha^\beta (x-\alpha)^m (x-\beta)^n \hspace{1pt} dx}$$ の形で出題されることも多いです。

この式の値を求めると

$$ \begin{aligned} \hspace{10pt} &\int_\alpha^\beta (x-\alpha)^m (x-\beta)^n \hspace{1pt} dx \hspace{10pt}\\[0.7em] \hspace{10pt} &= \frac{ m! n!}{(m+n+1)! } (\beta - \alpha)^{m+n+1} \hspace{10pt}\\[0.7em] \end{aligned} $$

となります。

(上式は$\hspace{2pt}B(m,n)\hspace{2pt}$を $${t = (\beta - \alpha)x + \alpha}$$ と置き換えることから導出されます。)

この式において$\hspace{2pt}(m,n) = (1,1)\hspace{2pt}$とすれば有名な$\displaystyle\hspace{1pt}\frac{1}{6}\hspace{1pt}$公式

$$\hspace{10pt}{\int_\alpha^\beta (x-\alpha) (x-\beta) \hspace{1pt} dx = \frac{1}{6 } (\beta - \alpha)^{3}}\hspace{10pt}$$

が導かれます。

また、$\hspace{2pt}(m,n) = (1,2)\hspace{2pt}$とすれば$\displaystyle\hspace{2pt}\frac{1}{12}\hspace{1pt}$公式

$$\hspace{10pt}{\int_\alpha^\beta (x-\alpha) (x-\beta)^2 \hspace{1pt} dx = \frac{1}{12 } (\beta - \alpha)^{4}}\hspace{10pt}$$

が導かれます。

答案にそのまま使用することはできませんが、覚えておくと$\displaystyle\hspace{1pt}\frac{1}{6}\hspace{1pt}$公式や$\displaystyle\hspace{1pt}\frac{1}{12}\hspace{1pt}$公式を確認したいときに便利です。
　

\({x}\)	\({\displaystyle 0 \to 1}\)
\({t}\)	\(\displaystyle{0 \to 1}\)

\({y}\)	\({\displaystyle 0 \to 1}\)
\({t}\)	\(\displaystyle{0 \to 1}\)

ベータ関数と面積・体積の問題