回転体を回転させた体積 | 積分ランダム問題集

【問題の答え】
　$\displaystyle \frac{64}{3}\pi $
　

【解答のポイント】
本問は回転体をさらに回転させたときの立体の体積を求める問題です。

正方形を回転させた立体$\hspace{1pt}A\hspace{1pt}$は、内側に円形の穴が開いた円を断面に持つ円柱であり、簡単にイメージすることができます。

この立体$\hspace{1pt}A\hspace{1pt}$をさらに回転させた立体$\hspace{1pt}B\hspace{1pt}$は具体的な形状をイメージしようとすると難しくなります。

そこで、まず以下のような立体$\hspace{1pt}A\hspace{1pt}$の内部の領域を表す不等式を作ります。 $$ \begin{dcases} & 1 \leqq x^2+z^2 \leqq 2^2 \\[1em] & 1 \leqq y \leqq 2 \end{dcases} $$

上記の不等式に対して平面$\hspace{2pt}x=t\hspace{2pt}$における立体$\hspace{1pt}A\hspace{2pt}$の断面を考えます。$\hspace{1pt}t\hspace{2pt}$を定数と考えて不等式を変形することがポイントです。

回転体の断面積は『$\hspace{2pt}\pi $(外径)² $ - \pi $ (内径)²』から計算できるため、不等式を変形して得られた断面を回転させたときの外径と内径を求めます。

このとき、$t\hspace{2pt}$の値によって断面の内径となる箇所が変わるため、場合分けが必要になります。

断面積を$\hspace{2pt}x\hspace{2pt}$方向の範囲で積分することで立体$\hspace{1pt}B\hspace{1pt}$の体積を求めます。
　

【問題の解答】
　問題 : 『$xyz\hspace{1pt}$空間において$\hspace{2pt}4\hspace{1pt}$個の点$\hspace{1pt}(0,1 ,1)\hspace{1pt},\hspace{1pt} (0,1 ,2) \hspace{1pt},$$\hspace{1pt} (0,2 ,1)\hspace{1pt},\hspace{1pt} (0,2 ,2)\hspace{2pt}$を頂点に持つ正方形を$\hspace{2pt}y\hspace{1pt}$軸の周りに回転させてできる立体を$\hspace{1pt}A\hspace{1pt}$とする. 立体$\hspace{1pt}A\hspace{2pt}$を$\hspace{2pt}x\hspace{1pt}$軸の周りに回転させたときの立体を$\hspace{1pt}B\hspace{1pt}$とするとき, 立体$\hspace{1pt}B\hspace{2pt}$の体積$\hspace{1pt}V\hspace{1pt}$を求めよ.』
　

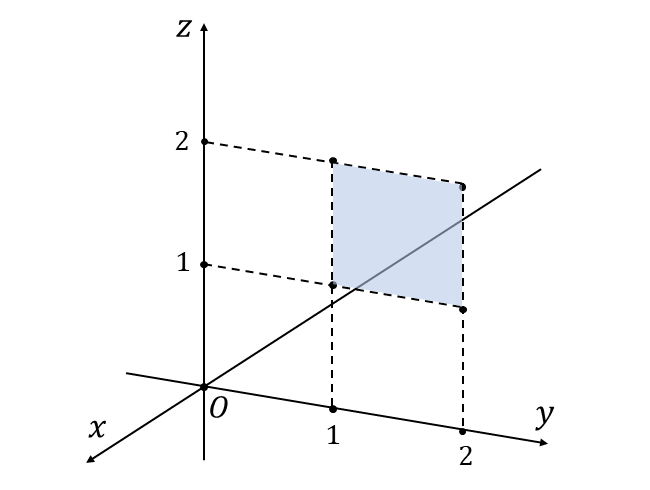
$\hspace{2pt}4\hspace{1pt}$個の点を図示すると、以下のようになります。回転させる正方形の図

まず、この正方形を$\hspace{2pt}y\hspace{1pt}$軸の周りに回転させた立体$\hspace{1pt}A\hspace{1pt}$の内部を表す連立不等式は

$$ \hspace{10pt} \begin{dcases} & 1 \leqq x^2+z^2 \leqq 2^2 \cdots(1)\hspace{10pt}\\[1em] & 1 \leqq y \leqq 2 \hspace{10pt}\\[1em] \end{dcases} $$

となります。

ここで、平面$\hspace{2pt}x = t$ $\hspace{2pt}(-2 \leqq t \leqq 2 )\hspace{2pt}$の断面を考えます。上記の(1)式において$\hspace{2pt}x=t\hspace{2pt}$とすると $$ 1- t^2 \leqq z^2 \leqq 4-t^2 $$ となります。すなわち、$z\hspace{2pt}$は以下の(2)式と(3)式を同時に満たします。 $$ \begin{dcases} & 1-t^2 \leqq z^2 \cdots(2)\\[1em] & -\sqrt{4-t^2} \leqq z \leqq \sqrt{4-t^2} \cdots(3)\\ \end{dcases} $$
　

ここで、(2)式は$\hspace{2pt} |t| \leqq 1\hspace{2pt}$のとき

$${\hspace{10pt}z \leqq -\sqrt{1-t^2} \hspace{1pt},\hspace{1pt}z \geqq \sqrt{1-t^2} \cdots(2)'\hspace{10pt}}$$

となります。

また、(2)式は$\hspace{2pt}|t| > 1 \hspace{2pt}$のとき、すべての実数$\hspace{1pt}z\hspace{1pt}$について成り立ちます。

よって、以下の場合に分けて体積を求めます。
　[1] $\hspace{3pt}|t| \leqq 1\hspace{2pt}$のとき
　[2] $\hspace{3pt}|t| > 1\hspace{2pt}$のとき
　

[1] $|t| \leqq 1\hspace{2pt}$のとき
　立体$\hspace{1pt}A\hspace{2pt}$の平面$\hspace{1pt}x=t\hspace{2pt}$における断面は以下の連立不等式によって表されます。

$$ \hspace{10pt} \begin{dcases} & z \leqq -\sqrt{1-t^2} \hspace{1pt},\hspace{1pt}z \geqq \sqrt{1-t^2} \cdots(2)'\hspace{10pt}\\[1em] & -\sqrt{4-t^2} \leqq z \leqq \sqrt{4-t^2} \cdots(3)\\[1em] & 1 \leqq y \leqq 2 \end{dcases} $$

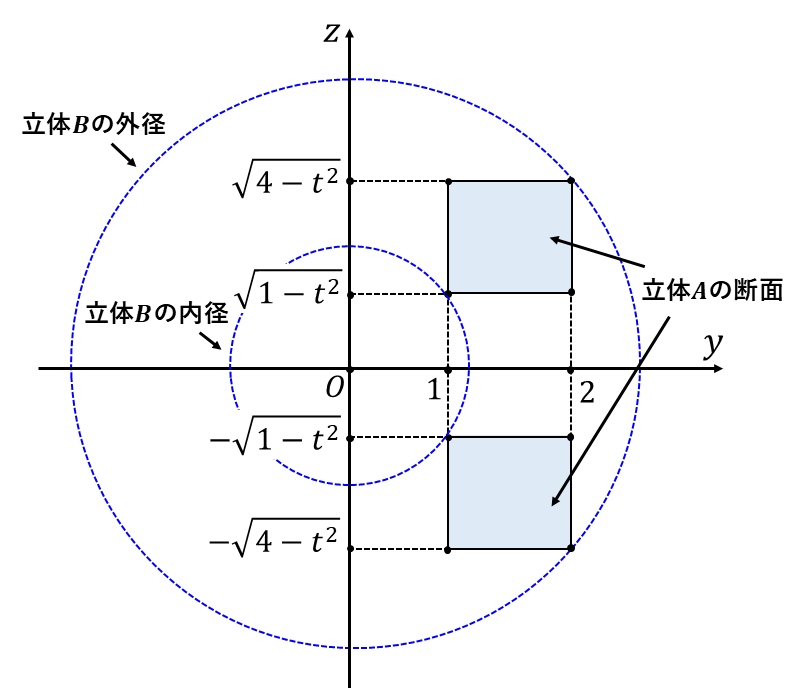
上式で表される領域を$\hspace{1pt}x=t\hspace{2pt}$における平面上に描くと以下の青く塗られた領域となります。平面を回転させたときのyz平面における断面

この断面を$\hspace{2pt}x\hspace{1pt}$軸を中心に回転させたときの外径は$\hspace{2pt}\sqrt{(\sqrt{4-t^2})^2 +2^2} = \sqrt{8-t^2 }\hspace{2pt}$、内径は$\hspace{2pt}\sqrt{(\sqrt{1-t^2})^2 +1^2} = \sqrt{2-t^2 }\hspace{2pt}$となります。

したがって、立体$\hspace{1pt}B\hspace{2pt}$の$\hspace{2pt}|t| \leqq 1\hspace{2pt}$の範囲の体積$\hspace{1pt}V_1\hspace{1pt}$は

$$ \begin{aligned} \hspace{10pt} V_1 =& \pi \int_{-1}^1((\sqrt{8-t^2 })^2 - (\sqrt{2-t^2 })^2)\hspace{1pt}dt\hspace{10pt}\\[1em] \hspace{10pt} =& \pi \int_{-1}^1 6\hspace{1pt}dt \hspace{10pt}\\[1em] \hspace{10pt} = & 6\pi \left[ t \right]_{-1}^1 \hspace{10pt}\\[1em] \hspace{10pt} = &12 \pi \\ \end{aligned} $$

[2] $|t| > 1\hspace{2pt}$のとき
　立体$\hspace{1pt}A\hspace{2pt}$の平面$\hspace{1pt}x=t\hspace{2pt}$における断面は以下の連立不等式によって表されます。

$$ \hspace{10pt} \begin{dcases} & -\sqrt{4-t^2} \leqq z \leqq \sqrt{4-t^2} \cdots(3)\hspace{10pt}\\[1em] & 1 \leqq y \leqq 2 \end{dcases} $$

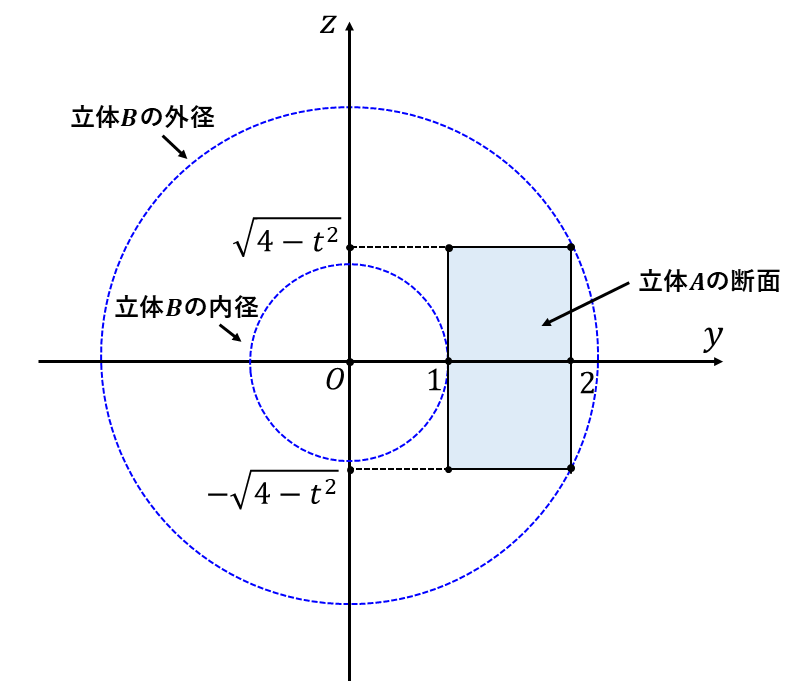
上式で表される領域を$\hspace{1pt}x=t\hspace{2pt}$における平面上に描くと以下の青く塗られた領域となります。平面を回転させたときのyz平面における断面_|t|>1の場合

この断面を$\hspace{2pt}x\hspace{1pt}$軸を中心に回転させたときの外径は$\hspace{2pt}\sqrt{(\sqrt{4-t^2})^2 +2^2} = \sqrt{8-t^2 }\hspace{2pt}$、内径は$\hspace{2pt}1\hspace{2pt}$となります。

したがって、立体$\hspace{1pt}B\hspace{2pt}$の$\hspace{2pt}|t| > 1\hspace{2pt}$の範囲の体積$\hspace{1pt}V_2\hspace{1pt}$は

$$ \begin{aligned} \hspace{10pt} V_2 =2 & \pi \int_{1}^2((\sqrt{8-t^2 })^2 - 1^2)\hspace{1pt}dt\hspace{10pt}\\[1em] \hspace{10pt} =& 2 \pi \int_{1}^2 (7 - t^2)\hspace{1pt}dt \hspace{10pt}\\[1em] \hspace{10pt} = &2 \pi \left[7t - \frac{1}{3}t^3 \right]_{1}^2 \hspace{10pt}\\[1em] \hspace{10pt} = &\frac{28}{3} \pi \\[1em] \end{aligned} $$

したがって、求める体積$\hspace{1pt}V\hspace{1pt}$は $$ \begin{aligned} V = & V_1 + V_2\\[0.5em] =& 12 \pi +\frac{28}{3} \pi \\[0.5em] =& \frac{64}{3} \pi \\ \end{aligned} $$ となります。
　

【入試本番に向けたアドバイス】
本問は、回転体をさらに回転させた立体の体積を求める問題です。

本問のように立体を具体的にイメージすることが難しい場合は、『立体を連立不等式で表し、平面で切った断面積から体積を求める』という手法が有効です。
　

本問では、二回目の回転の回転軸が$\hspace{1pt}x\hspace{1pt}$軸であることから、平面$\hspace{1pt}x=t\hspace{2pt}$における断面を考えています。

一方、回転体ではない問題の場合、立体の切り方として $${x = t \hspace{1pt},\hspace{1pt} y = t \hspace{1pt},\hspace{1pt} z = t}$$ の3つの選択肢があります。

断面を切る文字の選び方は、『その断面で切ると残りの文字の対称性が良くなる』や『その断面で切ると残りの文字の次数が小さくなる』ような文字を優先して$\hspace{2pt}t\hspace{2pt}$とおくようにします。
　

形をイメージすることの難しい立体の問題も『立体を連立不等式で表して体積を求める』ことで、単純な数式の処理で解くことができます。

この解法を知っているかどうかで問題の難易度が大きく変わるので、必ず解けるようにしておきましょう。
　