カージオイドの面積と回転体の体積
◆第問目!
(1) 線分\(\hspace{1pt}OP\hspace{1pt}\)と\(\hspace{2pt}x\hspace{1pt}\)軸のなす角度を\(\hspace{2pt}\theta\hspace{2pt}\)\(\hspace{2pt}(0 \leqq \theta < 2 \pi)\hspace{2pt}\)とするとき, 点\(\hspace{1pt}P\hspace{1pt}\)の座標\(\hspace{2pt}(x,y)\hspace{2pt}\)を\(\hspace{2pt}\theta\hspace{2pt}\)で表せ.
(2) 曲線\(\hspace{1pt}C\hspace{2pt}\)の概形を描け.
(3) 曲線\(\hspace{1pt}C\hspace{2pt}\)によって囲まれる面積\(\hspace{1pt}S\hspace{2pt}\)を求めよ.
(4) 曲線\(\hspace{1pt}C\hspace{2pt}\)を\(\hspace{2pt}x\hspace{1pt}\)軸の周りに回転させた回転体の体積\(\hspace{1pt}V\hspace{2pt}\)を求めよ.
(5) 曲線\(\hspace{1pt}C\hspace{2pt}\)の長さ\(\hspace{1pt}L\hspace{2pt}\)を求めよ.
まず、点\(\hspace{1pt}B\hspace{1pt}\)の座標を求めます。
円周上を動く点\(\hspace{1pt}B\hspace{1pt}\)の座標は、位置ベクトル\(\hspace{1pt}\overrightarrow{OB}\hspace{2pt}\)を
$${\overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB} }$$
と表すことで考えやすくなります。
次に、接線\(\hspace{1pt}l\hspace{1pt}\)の方程式を求めます。
接点\(\hspace{1pt}(x_1 , y_1)\hspace{1pt}\)における円\(\hspace{2pt}(x-a)^2+(y-b)^2=r^2\hspace{2pt}\)の接線の方程式
を用いることで接線\(\hspace{1pt}l\hspace{1pt}\)の方程式を求めることができます。
接線\(\hspace{1pt}l\hspace{1pt}\)の方程式が分かれば、点\(\hspace{1pt}P\hspace{1pt}\)と原点\(\hspace{1pt}O\hspace{1pt}\)の距離を求めることができます。
点\(\hspace{2pt}(x_2 , y_2)\hspace{2pt}\)と直線の方程式\(\hspace{2pt}ax+by+c=0\hspace{2pt}\)の距離を求める公式 $${\frac{|a x_2 + b y_2 + c|}{\sqrt{a^2+b^2}}}$$ から、点\(\hspace{1pt}P\hspace{1pt}\)と原点\(\hspace{1pt}O\hspace{1pt}\)の距離を求めることができます。
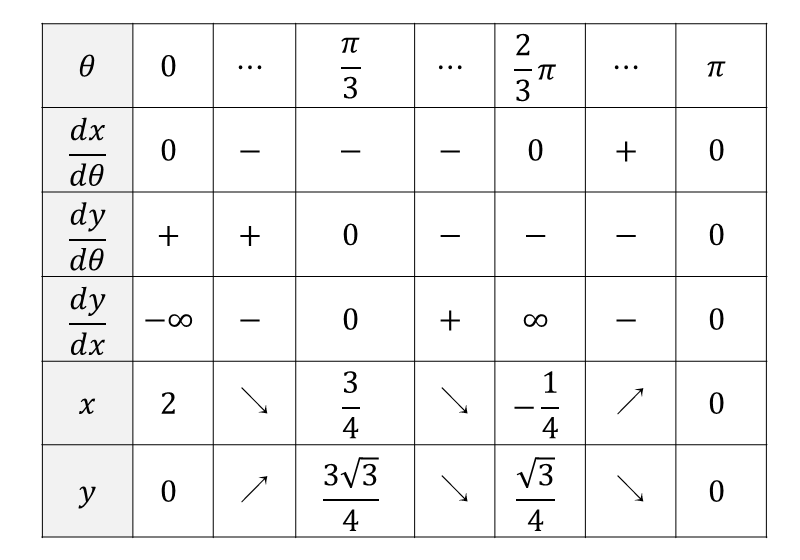
問題(1)の結果から\(\displaystyle \hspace{2pt}\frac{dx}{d\theta} , \frac{dy}{d\theta} , \frac{dy}{dx}\hspace{2pt}\)を求め、増減表を作ります。
曲線の対称性から、調べる\(\hspace{1pt}\theta\hspace{2pt}\)の範囲は\(\hspace{2pt}0 \leqq \theta \leqq \pi\hspace{2pt}\)となります。
問題(2)のグラフから、\(\displaystyle 0 \leqq \theta \leqq \frac{3}{2}\pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_1\)、\(\displaystyle \frac{3}{2}\pi \leqq \theta \leqq \pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_2\hspace{2pt}\)とし、以下のように積分区間を分けて計算します。
問題(2)のグラフから、\(\displaystyle 0 \leqq \theta \leqq \frac{3}{2}\pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_1\)、\(\displaystyle \frac{3}{2}\pi \leqq \theta \leqq \pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_2\hspace{2pt}\)とし、以下のように積分区間を分けて計算します。
求める曲線の長さ\(\displaystyle\hspace{2pt}L\hspace{2pt}\)は
から求められます。
【問題(1)の答え】
\(\displaystyle (x,y)=( (1 + \cos \theta)\cos \theta \hspace{1pt}, \hspace{1pt}(1 + \cos \theta)\sin \theta) \)
【問題(2)の答え】
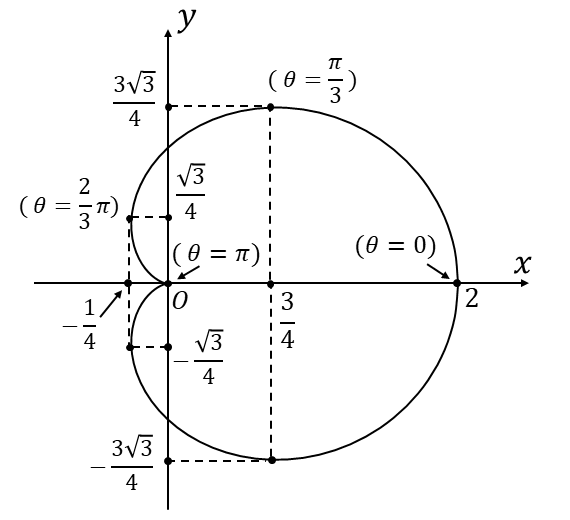
【問題(3)の答え】
\(\displaystyle \frac{3}{2}\pi\hspace{2pt}\)
【問題(4)の答え】
\( \displaystyle\frac{8}{3} \pi\hspace{2pt}\)
【問題(5)の答え】
\(8\hspace{2pt}\)
【解答のポイント】
本問は、カージオイドと呼ばれる曲線の概形・面積・体積・長さを求める問題です。
問題(1)は、曲線の座標を求める問題です。
円周上を動く点\(\hspace{1pt}B\hspace{1pt}\)の座標は、位置ベクトル\(\hspace{1pt}\overrightarrow{OB}\hspace{2pt}\)を
$${\overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB} }$$
と表すことで考えやすくなります。
問題(2)は曲線の概形を描く問題です。
曲線の概形は一部が折り返しのある形となり、\(\displaystyle\frac{dx}{d\theta} =0, \frac{dy}{d\theta}=0 \hspace{2pt}\)となる点の座標に加え、\(\displaystyle \frac{dy}{dx}\hspace{2pt}\)の極限の値も丁寧に調べる必要があります。
【問題(1)の解答】
問題 : 『\(xy\hspace{1pt}\)平面において点\(\hspace{1pt}A\hspace{1pt}(1 , 0)\hspace{2pt}\)が中心, 半径が\(\hspace{1pt}1\hspace{1pt}\)である円上に点\(\hspace{1pt}B\hspace{1pt}\)をとる. 点\(\hspace{1pt}B\hspace{1pt}\)を接点とする接線\(\hspace{1pt}l\hspace{1pt}\)に原点\(\hspace{1pt}O\hspace{1pt}\)から下した垂線の足を点\(\hspace{1pt}P\hspace{2pt}\)とする. 点\(\hspace{1pt}B\hspace{2pt}\)が円周上を動くとき, 点\(\hspace{1pt}P\hspace{1pt}\)の描く曲線を\(\hspace{1pt}C\hspace{2pt}\)とする.
(1) 線分\(\hspace{1pt}OP\hspace{1pt}\)と\(\hspace{2pt}x\hspace{1pt}\)軸のなす角度を\(\hspace{2pt}\theta\hspace{2pt}\)\(\hspace{2pt}(0 \leqq \theta < 2 \pi)\hspace{2pt}\)とするとき, 点\(\hspace{1pt}P\hspace{1pt}\)の座標\(\hspace{2pt}(x,y)\hspace{2pt}\)を\(\hspace{2pt}\theta\hspace{2pt}\)で表せ.
(2) 曲線\(\hspace{1pt}C\hspace{2pt}\)の概形を描け.
(3) 曲線\(\hspace{1pt}C\hspace{2pt}\)によって囲まれる面積\(\hspace{1pt}S\hspace{2pt}\)を求めよ.
(4) 曲線\(\hspace{1pt}C\hspace{2pt}\)を\(\hspace{2pt}x\hspace{1pt}\)軸の周りに回転させた回転体の体積\(\hspace{1pt}V\hspace{2pt}\)を求めよ.
(5) 曲線\(\hspace{1pt}C\hspace{2pt}\)の長さ\(\hspace{1pt}L\hspace{2pt}\)を求めよ.』
点\(\hspace{1pt}P\hspace{1pt}\)を図示すると以下のようになります。
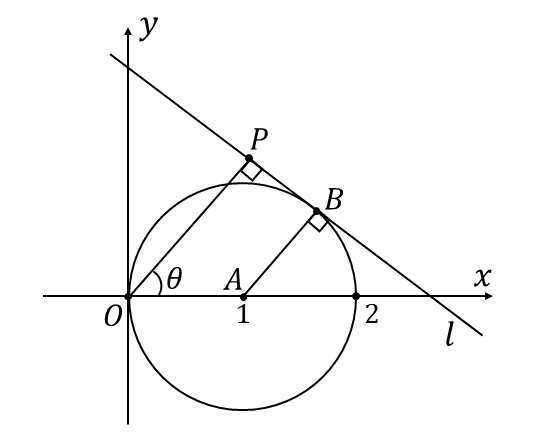
まず、点\(\hspace{1pt}B\hspace{1pt}\)の座標を求めます。
位置ベクトル\(\hspace{1pt}\overrightarrow{OB}\hspace{2pt}\)は以下のように表されます。
$${\overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB} }$$
\(\overrightarrow{OA} = (1,0)\hspace{2pt}, \hspace{2pt}\overrightarrow{AB} = (\cos \theta, \sin \theta )\hspace{2pt}\)であることから $$ \begin{aligned} \overrightarrow{OB} & =(1,0) + (\cos \theta, \sin \theta )\\[0.5em] & = (1 + \cos \theta, \sin \theta )\\ \end{aligned} $$ となります。
したがって、点\(\hspace{1pt}B\hspace{1pt}\)の座標は\(\hspace{2pt}(1 + \cos \theta, \sin \theta )\hspace{2pt}\)となります。
次に、点\(\hspace{1pt}P\hspace{1pt}\)の座標を求めます。
接点\(\hspace{1pt}(x_1 , y_1)\hspace{1pt}\)における円\(\hspace{2pt}(x-a)^2+(y-b)^2=r^2\hspace{2pt}\)の接線の方程式は
となります。
接線\(\hspace{1pt}l\hspace{1pt}\)の方程式は、接点が\(\hspace{1pt}(1 + \cos \theta, \sin \theta)\hspace{1pt}\)、接する円が\(\hspace{2pt}(x-1)^2+y^2=1\hspace{2pt}\)であることから
となります。
よって、原点\(\hspace{2pt}O\hspace{1pt}\)と接線\(\hspace{1pt}l\hspace{1pt}\)の距離は
となります。
したがって、点\(\hspace{1pt}P\hspace{1pt}\)の座標は
となります。
【問題(2)の解答】
問題 : 『\(xy\hspace{1pt}\)平面において点\(\hspace{1pt}A\hspace{1pt}(1 , 0)\hspace{2pt}\)が中心, 半径が\(\hspace{1pt}1\hspace{1pt}\)である円上に点\(\hspace{1pt}B\hspace{1pt}\)をとる. 点\(\hspace{1pt}B\hspace{1pt}\)を接点とする接線\(\hspace{1pt}l\hspace{1pt}\)に原点\(\hspace{1pt}O\hspace{1pt}\)から下した垂線の足を点\(\hspace{1pt}P\hspace{2pt}\)とする. 点\(\hspace{1pt}B\hspace{2pt}\)が円周上を動くとき, 点\(\hspace{1pt}P\hspace{1pt}\)の描く曲線を\(\hspace{1pt}C\hspace{2pt}\)とする.
(1) 線分\(\hspace{1pt}OP\hspace{1pt}\)と\(\hspace{2pt}x\hspace{1pt}\)軸のなす角度を\(\hspace{2pt}\theta\hspace{2pt}\)\(\hspace{2pt}(0 \leqq \theta < 2 \pi)\hspace{2pt}\)とするとき, 点\(\hspace{1pt}P\hspace{1pt}\)の座標\(\hspace{2pt}(x,y)\hspace{2pt}\)を\(\hspace{2pt}\theta\hspace{2pt}\)で表せ.
(2) 曲線\(\hspace{1pt}C\hspace{2pt}\)の概形を描け.
(3) 曲線\(\hspace{1pt}C\hspace{2pt}\)によって囲まれる面積\(\hspace{1pt}S\hspace{2pt}\)を求めよ.
(4) 曲線\(\hspace{1pt}C\hspace{2pt}\)を\(\hspace{2pt}x\hspace{1pt}\)軸の周りに回転させた回転体の体積\(\hspace{1pt}V\hspace{2pt}\)を求めよ.
(5) 曲線\(\hspace{1pt}C\hspace{2pt}\)の長さ\(\hspace{1pt}L\hspace{2pt}\)を求めよ.』
問題(1)で求めた\(\hspace{2pt}(x,y)\hspace{2pt}\)において\(\hspace{2pt}\theta\hspace{2pt}\)に\(\hspace{2pt}-\theta\hspace{2pt}\)を代入すると\(\hspace{2pt}(x,y)\hspace{2pt}\)が\(\hspace{2pt}(x,-y)\hspace{2pt}\)となることから、曲線\(\hspace{2pt}C\hspace{2pt}\)は\(\hspace{2pt}x\hspace{1pt}\)軸に関して対称となります。
よって、\(0 \leqq \theta \leqq \pi\hspace{2pt}\)の範囲を調べます。
グラフの概形を求めるために、まず\(\displaystyle\hspace{2pt}\frac{dx}{d\theta} \hspace{1pt},\hspace{1pt} \frac{dy}{d\theta}\hspace{2pt}\)を求めます。
となります。
\(0 \leqq \theta \leqq \pi\hspace{2pt}\)において\(\displaystyle\hspace{2pt}\frac{dx}{d\theta} =0\hspace{2pt}\)を解くと $${\sin \theta = 0 \hspace{1pt}, \hspace{1pt} \cos \theta = - \frac{1}{2}}$$ より $${\theta = 0 \hspace{1pt}, \hspace{1pt}\frac{2}{3}\pi \hspace{1pt}, \hspace{1pt}\pi }$$ となります。
\(\displaystyle\hspace{2pt}\frac{dx}{d\theta} =0\hspace{2pt}\)となる座標を求めると $${\left( 2\hspace{1pt}, 0\hspace{1pt}\right) , \left( -\frac{1}{4}\hspace{1pt}, \frac{\sqrt{3}}{4}\hspace{1pt}\right) , \left( 0\hspace{1pt},0\hspace{1pt}\right) }$$ となります。
また、\(0 \leqq \theta \leqq \pi\hspace{2pt}\)において\(\displaystyle\hspace{2pt}\frac{dy}{d\theta} =0\hspace{2pt}\)を解くと $${\cos \theta = \frac{1}{2} \hspace{1pt}, \hspace{1pt} \cos \theta = - 1}$$ より $${\theta = \frac{\pi}{3} \hspace{1pt}, \hspace{1pt}\pi }$$ となります。
\(\displaystyle\hspace{2pt}\frac{dy}{d\theta} =0\hspace{2pt}\)となる座標を求めると $${\left( \frac{3}{4}\hspace{1pt}, \frac{3\sqrt{3}}{4}\hspace{1pt}\right) \hspace{1pt},\hspace{1pt} \left( 0\hspace{1pt},0\hspace{1pt}\right) }$$ となります。
また、\(\displaystyle \frac{dy}{dx}\hspace{2pt}\)を求めると $$ \begin{aligned} \hspace{10pt}\frac{dy}{dx} & = \Large{\frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}}\\[1.5em] & =- \frac{ \cos \theta + \cos 2\theta}{\sin \theta + \sin 2\theta}\\[1em] & =- \frac{ 2\cos \frac{3}{2}\theta \cos \frac{\theta}{2}}{2\sin \frac{3}{2}\theta \cos \frac{\theta}{2}}\\[1em] & =- \frac{ \cos \frac{3}{2}\theta}{\sin \frac{3}{2}\theta }\\[1em] \end{aligned} $$ となります。
(上記の変形は和積の公式
を用いて計算しています。)
よって $$ \begin{aligned} \hspace{10pt}\lim_{\theta \rightarrow + 0} \frac{dy}{dx} & = \lim_{\theta \rightarrow + 0}\left(- \frac{ \cos \frac{3}{2}\theta}{\sin \frac{3}{2}\theta }\right)\\[0.5em] & = - \infty\\[0.5em] \end{aligned} $$ となります。
また $$ \begin{aligned} \hspace{10pt}\lim_{\theta \rightarrow \pi} \frac{dy}{dx} & = \lim_{\theta \rightarrow \pi}\left(- \frac{ \cos \frac{3}{2}\theta}{\sin \frac{3}{2}\theta }\right)\\[0.5em] & = 0\\[1em] \end{aligned} $$ となります。
また $$ \begin{aligned} \hspace{10pt}\lim_{\theta \rightarrow \frac{\pi}{3}} \frac{dy}{dx} & = \lim_{\theta \rightarrow \frac{\pi}{3}} \left(-\frac{ \cos \frac{3}{2}\theta}{\sin \frac{3}{2}\theta }\right)\\[0.5em] & = 0\\[1em] \end{aligned} $$ となります。
また $$ \begin{aligned} \hspace{10pt}\lim_{\theta \rightarrow \frac{2}{3}\pi \pm 0} \frac{dy}{dx} & = \left(\lim_{\theta \rightarrow \frac{2}{3}\pi \pm 0} -\frac{ \cos \frac{3}{2}\theta}{\sin \frac{3}{2}\theta }\right)\\[0.5em] & = \pm \infty\\[1em] \end{aligned} $$ となります。
以上から、増減表は以下のようになります。
よって、グラフの概形は以下のようになります。

【問題(3)の解答】
問題 : 『\(xy\hspace{1pt}\)平面において点\(\hspace{1pt}A\hspace{1pt}(1 , 0)\hspace{2pt}\)が中心, 半径が\(\hspace{1pt}1\hspace{1pt}\)である円上に点\(\hspace{1pt}B\hspace{1pt}\)をとる. 点\(\hspace{1pt}B\hspace{1pt}\)を接点とする接線\(\hspace{1pt}l\hspace{1pt}\)に原点\(\hspace{1pt}O\hspace{1pt}\)から下した垂線の足を点\(\hspace{1pt}P\hspace{2pt}\)とする. 点\(\hspace{1pt}B\hspace{2pt}\)が円周上を動くとき, 点\(\hspace{1pt}P\hspace{1pt}\)の描く曲線を\(\hspace{1pt}C\hspace{2pt}\)とする.
(1) 線分\(\hspace{1pt}OP\hspace{1pt}\)と\(\hspace{2pt}x\hspace{1pt}\)軸のなす角度を\(\hspace{2pt}\theta\hspace{2pt}\)\(\hspace{2pt}(0 \leqq \theta < 2 \pi)\hspace{2pt}\)とするとき, 点\(\hspace{1pt}P\hspace{1pt}\)の座標\(\hspace{2pt}(x,y)\hspace{2pt}\)を\(\hspace{2pt}\theta\hspace{2pt}\)で表せ.
(2) 曲線\(\hspace{1pt}C\hspace{2pt}\)の概形を描け.
(3) 曲線\(\hspace{1pt}C\hspace{2pt}\)によって囲まれる面積\(\hspace{1pt}S\hspace{2pt}\)を求めよ.
(4) 曲線\(\hspace{1pt}C\hspace{2pt}\)を\(\hspace{2pt}x\hspace{1pt}\)軸の周りに回転させた回転体の体積\(\hspace{1pt}V\hspace{2pt}\)を求めよ.
(5) 曲線\(\hspace{1pt}C\hspace{2pt}\)の長さ\(\hspace{1pt}L\hspace{2pt}\)を求めよ.』
問題(2)のグラフから、\(\displaystyle 0 \leqq \theta \leqq \frac{2}{3}\pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_1\hspace{2pt}\)、\(\displaystyle \frac{2}{3}\pi \leqq \theta \leqq \pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_2\hspace{2pt}\)とします。
求める面積\(\displaystyle\hspace{2pt}S\hspace{2pt}\)は
となります。
ここで $${\frac{dx}{d\theta} = - \sin \theta (1+2 \cos \theta)}$$ であることから\(\hspace{2pt}dx = - \sin \theta (1+2 \cos \theta) d\theta \hspace{2pt}\)と表せます。
よって、求める面積\(\displaystyle\hspace{2pt}S\hspace{2pt}\)は
と求められます。
【別解】
もしくは、極座標の面積公式から
と求められます。
(ただし、大学入試では極座標の面積公式は証明なしでは使用できないため、検算などの目的でのみ使用します。)
【問題(4)の解答】
問題 : 『\(xy\hspace{1pt}\)平面において点\(\hspace{1pt}A\hspace{1pt}(1 , 0)\hspace{2pt}\)が中心, 半径が\(\hspace{1pt}1\hspace{1pt}\)である円上に点\(\hspace{1pt}B\hspace{1pt}\)をとる. 点\(\hspace{1pt}B\hspace{1pt}\)を接点とする接線\(\hspace{1pt}l\hspace{1pt}\)に原点\(\hspace{1pt}O\hspace{1pt}\)から下した垂線の足を点\(\hspace{1pt}P\hspace{2pt}\)とする. 点\(\hspace{1pt}B\hspace{2pt}\)が円周上を動くとき, 点\(\hspace{1pt}P\hspace{1pt}\)の描く曲線を\(\hspace{1pt}C\hspace{2pt}\)とする.
(1) 線分\(\hspace{1pt}OP\hspace{1pt}\)と\(\hspace{2pt}x\hspace{1pt}\)軸のなす角度を\(\hspace{2pt}\theta\hspace{2pt}\)\(\hspace{2pt}(0 \leqq \theta < 2 \pi)\hspace{2pt}\)とするとき, 点\(\hspace{1pt}P\hspace{1pt}\)の座標\(\hspace{2pt}(x,y)\hspace{2pt}\)を\(\hspace{2pt}\theta\hspace{2pt}\)で表せ.
(2) 曲線\(\hspace{1pt}C\hspace{2pt}\)の概形を描け.
(3) 曲線\(\hspace{1pt}C\hspace{2pt}\)によって囲まれる面積\(\hspace{1pt}S\hspace{2pt}\)を求めよ.
(4) 曲線\(\hspace{1pt}C\hspace{2pt}\)を\(\hspace{2pt}x\hspace{1pt}\)軸の周りに回転させた回転体の体積\(\hspace{1pt}V\hspace{2pt}\)を求めよ.
(5) 曲線\(\hspace{1pt}C\hspace{2pt}\)の長さ\(\hspace{1pt}L\hspace{2pt}\)を求めよ.』
問題(2)のグラフから、\(\displaystyle 0 \leqq \theta \leqq \frac{2}{3}\pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_1\hspace{2pt}\)、\(\displaystyle \frac{2}{3}\pi \leqq \theta \leqq \pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_2\hspace{2pt}\)とします。
求める体積\(\displaystyle\hspace{2pt}V\hspace{2pt}\)は
ここで、\(\cos \theta = t\hspace{2pt}\)とおきます。
両辺を微分すると\(\displaystyle \hspace{2pt} \frac{dt}{d\theta} = - \sin \theta\hspace{2pt}\)であることから\(\hspace{2pt}dt = - \sin \theta d\theta \hspace{2pt}\)と表せます。
【問題(5)の解答】
問題 : 『\(xy\hspace{1pt}\)平面において点\(\hspace{1pt}A\hspace{1pt}(1 , 0)\hspace{2pt}\)が中心, 半径が\(\hspace{1pt}1\hspace{1pt}\)である円上に点\(\hspace{1pt}B\hspace{1pt}\)をとる. 点\(\hspace{1pt}B\hspace{1pt}\)を接点とする接線\(\hspace{1pt}l\hspace{1pt}\)に原点\(\hspace{1pt}O\hspace{1pt}\)から下した垂線の足を点\(\hspace{1pt}P\hspace{2pt}\)とする. 点\(\hspace{1pt}B\hspace{2pt}\)が円周上を動くとき, 点\(\hspace{1pt}P\hspace{1pt}\)の描く曲線を\(\hspace{1pt}C\hspace{2pt}\)とする.
(1) 線分\(\hspace{1pt}OP\hspace{1pt}\)と\(\hspace{2pt}x\hspace{1pt}\)軸のなす角度を\(\hspace{2pt}\theta\hspace{2pt}\)\(\hspace{2pt}(0 \leqq \theta < 2 \pi)\hspace{2pt}\)とするとき, 点\(\hspace{1pt}P\hspace{1pt}\)の座標\(\hspace{2pt}(x,y)\hspace{2pt}\)を\(\hspace{2pt}\theta\hspace{2pt}\)で表せ.
(2) 曲線\(\hspace{1pt}C\hspace{2pt}\)の概形を描け.
(3) 曲線\(\hspace{1pt}C\hspace{2pt}\)によって囲まれる面積\(\hspace{1pt}S\hspace{2pt}\)を求めよ.
(4) 曲線\(\hspace{1pt}C\hspace{2pt}\)を\(\hspace{2pt}x\hspace{1pt}\)軸の周りに回転させた回転体の体積\(\hspace{1pt}V\hspace{2pt}\)を求めよ.
(5) 曲線\(\hspace{1pt}C\hspace{2pt}\)の長さ\(\hspace{1pt}L\hspace{2pt}\)を求めよ.』
求める曲線の長さ\(\displaystyle\hspace{2pt}L\hspace{2pt}\)は
と求められます。
【入試本番に向けたアドバイス】
本問は、カージオイドと呼ばれる曲線の面積・体積・長さを求める問題です。
カージオイドは\(\hspace{2pt}a\hspace{2pt}\)を正の定数とすると極方程式により $${r = a(1 + \cos \theta)\hspace{6pt}(0 \leqq \theta < 2\pi)}$$ と表されます。
問題(1)では、カージオイドを直交座標系で表した $$ \begin{dcases} & x = a(1 + \cos \theta)\cos \theta\\[0.5em] & y = a(1 + \cos \theta)\sin \theta\\ \end{dcases} $$
の形式で導出しました。
本問は『曲線の面積・体積・長さを求める』というシンプルな設問ですが、極方程式で表される曲線は計算がややこしくなり、難関大学の問題としてもよく取り上げられるテーマの一つです。
計算過程で躓きやすいポイントを解説します。
①折り返しのある部分を引き算する
問題(3)では以下のグラフから面積を求めました。

求める面積\(\displaystyle\hspace{2pt}S\hspace{2pt}\)は、\(\displaystyle 0 \leqq \theta \leqq \frac{2}{3}\pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_1\hspace{2pt}\)、\(\displaystyle \frac{2}{3}\pi \leqq \theta \leqq \pi\hspace{2pt}\)の範囲の曲線を\(\hspace{2pt}y_2\hspace{2pt}\)とすると
となります。
曲線が\(\displaystyle \hspace{2pt}\frac{2}{3}\pi \leqq \theta \leqq \pi\hspace{2pt}\)の範囲で折り返されていることから、上側の関数と下側の関数に分けて面積を計算しています。
問題(4)の回転体の体積を求めるときも同様に上側と下側の関数に分けて計算します。
②積分区間の変化に注意する
上記の面積の式を
$${\frac{dx}{d\theta} = - \sin \theta (1+2 \cos \theta)}$$
であることから\(\hspace{2pt}dx = - \sin \theta (1+2 \cos \theta) d\theta \hspace{2pt}\)から変形すると
であることから
となります。
このように、\(\displaystyle 0 \leqq \theta \leqq \frac{3}{2}\pi\hspace{2pt}\)の範囲か\(\displaystyle \hspace{2pt}\frac{3}{2}\pi \leqq \theta \leqq \pi\hspace{2pt}\)の範囲かで、\(\hspace{2pt}x\hspace{2pt}\)と\(\hspace{2pt}\theta\hspace{2pt}\)の積分区間の対応する値が変わる点に注意が必要です。
特に、\(\displaystyle 0 \leqq \theta \leqq \frac{3}{2}\pi\hspace{2pt}\)の範囲では\(\hspace{2pt}x\hspace{2pt}\)から\(\hspace{2pt}\theta\hspace{2pt}\)に変換したときに積分区間の大小関係が逆になる点が間違いやすいため気を付けましょう。
【問題の種類を絞る】