直線を回転させてできる曲線に囲まれた体積の問題と解き方

【問題の答え】
　$\displaystyle \frac{4}{3}\pi $
　

【解答のポイント】
直線$\hspace{1pt}l\hspace{2pt}$と回転軸である$\hspace{2pt}z\hspace{1pt}$軸はねじれの位置にあり、作図から具体的な形状を描くことは難しいです。

そこで『直線$\hspace{1pt}l\hspace{1pt}$を回転させる』と考えるのではなく、『直線$\hspace{1pt}l\hspace{1pt}$上の点を回転させた断面積を求め、回転軸方向に積分する』と考えます。

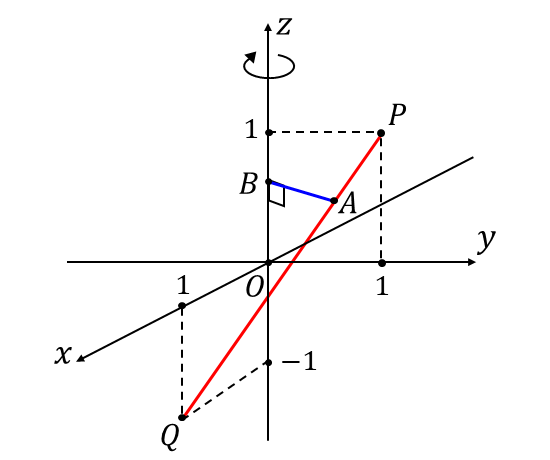
まず、以下の図のように平面$\hspace{2pt}z = t\hspace{2pt}$と直線$\hspace{1pt}l\hspace{1pt}$の交点を点$\hspace{1pt}A\hspace{2pt}$、$\hspace{2pt}z = t\hspace{2pt}$と$\hspace{1pt}z\hspace{1pt}$軸の交点を点$\hspace{1pt}B\hspace{2pt}$とします。直線が回転してできる部分の体積_ポイント解説

次に、点$\hspace{1pt}A\hspace{1pt}$の座標を$\hspace{2pt}t\hspace{2pt}$で表します。

このとき、点$\hspace{1pt}P\hspace{1pt}$と点$\hspace{2pt}Q\hspace{2pt}$を通る直線の式を作る必要がありますが、空間の直線を考えるときはベクトル方程式が便利です。

ベクトル方程式から、媒介変数を$\hspace{2pt}s\hspace{2pt}$とすると $${\overrightarrow{OA} = \overrightarrow{OP} + s \overrightarrow{PQ}}$$ と表すことができます。

ベクトル方程式を用いて点$\hspace{1pt}A\hspace{1pt}$の座標を$\hspace{2pt}t\hspace{2pt}$で表し、線分$\hspace{1pt}\overline{AB}\hspace{1pt}$が$\hspace{2pt}z\hspace{1pt}$軸回りに回転すると考えることで、断面積$\hspace{2pt}S(t)\hspace{2pt}$を求めます。

断面積$\hspace{1pt}S(t)\hspace{1pt}$を$\hspace{2pt}[-1 , 1]\hspace{2pt}$の区間で積分することで立体の体積を求めます。
　

【問題の解答】
　問題 : 『$xyz\hspace{1pt}$空間において点$\hspace{1pt}P(0,1,1)\hspace{1pt}$と点$\hspace{2pt}Q(1,0,-1)\hspace{2pt}$を通る直線を$\hspace{2pt}l\hspace{2pt}$とする. 直線$\hspace{1pt}l\hspace{1pt}$を$\hspace{2pt}z\hspace{1pt}$軸を中心に回転させてできる曲面と平面$\hspace{2pt}z=1 , z=-1\hspace{2pt}$に囲まれてできる立体の体積を求めよ.』
　

平面$\hspace{2pt}z = t\hspace{2pt}$と直線$\hspace{1pt}l\hspace{1pt}$の交点を点$\hspace{2pt}A(x,y,t)\hspace{2pt}$、$\hspace{2pt}z = t\hspace{2pt}$と$\hspace{1pt}z\hspace{1pt}$軸の交点を点$\hspace{2pt}B(0,0,t)\hspace{2pt}$とします。直線が回転してできる部分の体積

ベクトル方程式から、媒介変数を$\hspace{2pt}s\hspace{2pt}$とすると $${\overrightarrow{OA} = \overrightarrow{OP} + s \overrightarrow{PQ}}$$ であることから $$ \begin{aligned} \overrightarrow{OA} & = (0,1,1) + s(1,-1,-2)\\[1em] & = (s\hspace{1pt} ,\hspace{1pt} 1-s\hspace{1pt} ,\hspace{1pt} 1-2s) \\ \end{aligned} $$ となります。

つまり、点$\hspace{1pt}A\hspace{1pt}$の$\hspace{2pt}z\hspace{2pt}$座標の値が$\hspace{2pt}t\hspace{2pt}$であるとき $${t = 1 -2s}$$ すなわち $${s = \frac{1-t}{2}}$$ となります。

よって、点$\hspace{1pt}A\hspace{1pt}$の座標を$\hspace{2pt}t\hspace{2pt}$により表すと $${A\left (\frac{1-t}{2} \hspace{1pt},\hspace{1pt} \frac{1+t}{2} \hspace{1pt}, \hspace{1pt} t \right )}$$ となります。

$\hspace{2pt}z = t\hspace{2pt}$における断面積$\hspace{2pt}S(t)\hspace{2pt}$は、線分$\hspace{2pt}\overline{AB}\hspace{2pt}$を半径とする円の面積であるので

$$ \begin{aligned} \hspace{10pt} S(t) & = \pi (\overline{AB})^2\\[1em] & = \pi (\sqrt{x^2 + y^2})^2 \\[1em] & = \pi \left \{\left ( \frac{1-t}{2} \right )^2 + \left ( \frac{1+t}{2} \right )^2 \right \} \hspace{10pt}\\[1em] \end{aligned} $$

となります。

よって、求める体積は

$$ \begin{aligned} \hspace{10pt} V & = \pi \int_{-1}^1\left \{\left ( \frac{1-t}{2} \right )^2 + \left ( \frac{1+t}{2} \right )^2 \right \}\hspace{1pt}dt \hspace{10pt}\\[1em] & = \frac{\pi}{4} \int_{-1}^1 \{\left ( 1-t \right )^2 + \left ( 1+t \right )^2 \}\hspace{1pt}dt \hspace{10pt}\\[1em] & = \frac{\pi}{4} \left [- \frac{1}{3}(1-t)^3 + \frac{1}{3}(1+t)^3 \right ]_{-1}^1 \hspace{10pt}\\[1em] & = \frac{\pi}{4} \left ( \frac{8}{3} + \frac{8}{3}\right )\\[1em] & = \frac{4}{3}\pi \\[1em] \end{aligned} $$

と求められます。
　

【入試本番に向けたアドバイス】
本問は、直線を回転させた部分の体積を求める問題です。

回転体の体積を求める場合、まず作図により概形を把握することが基本です。

しかし、本問は直線$\hspace{1pt}l\hspace{2pt}$と回転軸がねじれの位置にあり、作図から具体的な形状を描くことは難しいです。

このような場合は無理に作図をする必要はなく、数式として処理していく方が上手くいくパターンが多いです。

回転体の体積は、回転軸に対して垂直な平面で切ったときの外径と内径の座標が分かれば求めることができます。

そのため、例えば回転軸に対して垂直な平面を$\hspace{2pt}z=t\hspace{2pt}$としたとき、外径と内径の座標を$\hspace{2pt}t\hspace{2pt}$で表すことを目標に数式として処理していきましょう。

数学Ⅲの面積・体積の問題は『作図から形状を読み取るパターン』と『作図せずに数式として処理するパターン』とがあり、問題文から見極めるように意識して問題を解きましょう。
　